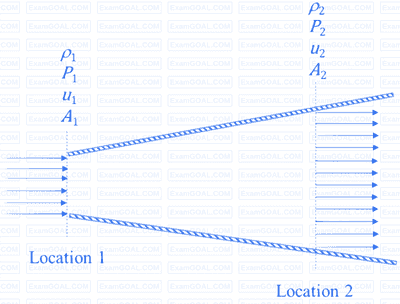
Consider an isentropic flow of air (ratio of specific heats = 1.4) through a duct as shown in the figure.

The variations in the flow across the cross-section are negligible. The flow conditions at Location 1 are given as follows:

𝑃₁ = 100 kPa, 𝜌₁ = 1.2 kg/m³ , 𝑢₁= 400 m/s

The duct cross-sectional area at Location 2 is given by A₂ = 2A₁, where A₁ denotes the duct cross-sectional area at Location 1. Which one of the given statements about the velocity 𝑢₂ and pressure 𝑃₂ at Location 2 is TRUE? 

The velocity field of a certain two-dimensional flow is given by

V(𝑥, 𝑦) = 𝑘(𝑥𝑖̂ − 𝑦𝑗̂)

where 𝑘 = 2 s^-1. The coordinates 𝑥 and 𝑦 are in meters. Assume gravitational effects to be negligible.

If the density of the fluid is 1000 kg/m³ and the pressure at the origin is 100 kPa, the pressure at the location (2 m, 2 m) is _____________ kPa.

(Answer in integer)

Consider a unidirectional fluid flow with the velocity field given by

V(𝑥, 𝑦, 𝑧, 𝑡) = 𝑢(𝑥, 𝑡) 𝑖̂

where 𝑢(0,𝑡) = 1. If the spatially homogeneous density field varies with time 𝑡 as

𝜌(𝑡) = 1 + 0.2𝑒^−𝑡

the value of 𝑢(2, 1) is ______________. (Rounded off to two decimal places) Assume all quantities to be dimensionless.

The figure shows two fluids held by a hinged gate. The atmospheric pressure is P_a = 100 kPa. The moment per unit width about the base of the hinge is ____________ kNm/m. (Rounded off to one decimal place)

Take the acceleration due to gravity to be g = 9.8 m/s².