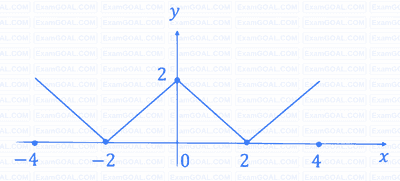
The figure shows the plot of a function over the interval [-4, 4]. Which one of the options given CORRECTLY identifies the function?

A vector field

𝐁(𝑥, 𝑦, 𝑧) = 𝑥 𝑖̂ + 𝑦 ĵ − 2𝑧 k̂

is defined over a conical region having height ℎ = 2, base radius 𝑟 = 3 and axis along z, as shown in the figure. The base of the cone lies in the x-y plane and is centered at the origin.

If 𝒏 denotes the unit outward normal to the curved surface 𝑆 of the cone, the value of the integral

$\rm \int_SB.n\ dS$

equals _________ . (Answer in integer)

A linear transformation maps a point (𝑥, 𝑦) in the plane to the point (𝑥̂, 𝑦̂) according to the rule

𝑥̂ = 3𝑦, 𝑦̂ = 2𝑥.

Then, the disc 𝑥² + 𝑦² ≤ 1 gets transformed to a region with an area equal to _________ . (Rounded off to two decimals)

Use π = 3.14. 

The value of k that makes the complex-valued function

𝑓(𝑧) = 𝑒−𝑘𝑥 (cos 2𝑦 − 𝑖 sin 2𝑦)

analytic, where 𝑧 = 𝑥 + 𝑖𝑦, is _________.

(Answer in integer)