1
GATE ME 2015 Set 1
Numerical
+2
-0
A cantilever beam with flexural rigidity of 200 N.m2 is loaded as shown in the figure. The deflection (in mm) at the tip of the beam is _______ .


Your input ____
2
GATE ME 2015 Set 1
Numerical
+1
-0
Consider a steel (Young’s modulus $$E = 200$$ $$GP$$a) column hinged on both sides. Its height is $$1.0$$ $$m$$ and cross-section is $$10 mm$$ $$ \times $$ $$20 mm$$. The lowest Euler critical buckling load (in $$N$$) is __________ .
Your input ____
3
GATE ME 2015 Set 1
Numerical
+1
-0
A wheel of radius r rolls without slipping on a horizontal surface shown below. If the velocity of point P is 10m/s in the horizontal direction, the magnitude of velocity of point Q (in m/s) is ______
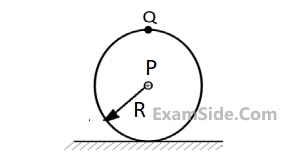

Your input ____
4
GATE ME 2015 Set 1
MCQ (Single Correct Answer)
+2
-0.6
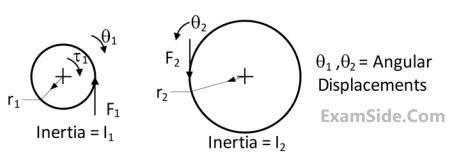
A pinion with radius $${r_1}$$, and inertia $${{\rm I}_1}$$ is driving a gear with radius $${r_2}$$ and inertia $${{\rm I}_2}$$ . Torque $${\tau _1}$$ is applied on pinion. The following are free body diagrams of pinion and gear showing important forces ($${F_1}$$and $${F_2}$$) of interaction. Which of the following relations hold true?

Paper analysis
Total Questions
Engineering Mathematics
12
Engineering Mechanics
3
Fluid Mechanics
5
Heat Transfer
4
Industrial Engineering
2
Machine Design
3
Production Engineering
11
Strength of Materials
3
Theory of Machines
6
Thermodynamics
5
More papers of GATE ME
GATE ME 2025
GATE ME 2024
GATE ME 2023
GATE ME 2022 Set 2
GATE ME 2022 Set 1
GATE ME 2020 Set 2
GATE ME 2020 Set 1
GATE ME 2019 Set 1
GATE ME 2019 Set 2
GATE ME 2018 Set 2
GATE ME 2018 Set 1
GATE ME 2017 Set 2
GATE ME 2017 Set 1
GATE ME 2016 Set 1
GATE ME 2016 Set 3
GATE ME 2016 Set 2
GATE ME 2015 Set 2
GATE ME 2015 Set 1
GATE ME 2015 Set 3
GATE ME 2014 Set 1
GATE ME 2014 Set 4
GATE ME 2014 Set 2
GATE ME 2014 Set 3
GATE ME 2014 Set
GATE ME 2014
GATE ME 2013
GATE ME 2012
GATE ME 2011
GATE ME 2010
GATE ME 2009
GATE ME 2008
GATE ME 2007
GATE ME 2006
GATE ME 2005
GATE ME 2004
GATE ME 2003
GATE ME 2002
GATE ME 2001
GATE ME 2000
GATE ME 1999
GATE ME 1998
GATE ME 1997
GATE ME 1996
GATE ME 1995
GATE ME 1994
GATE ME 1993
GATE ME 1992
GATE ME 1991
GATE ME 1990
GATE ME 1989
GATE ME 1988
GATE ME 1987
GATE ME
Papers
2025
2024
2023
2014
2013
2012
2011
2010
2009
2008
2007
2006
2005
2004
2003
2002
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
1991
1990
1989
1988
1987