Calculate number of molecules present in 5.4 g of urea (Molar mass of urea $=60 \mathrm{~g} \mathrm{~mol}^{-1}$ )

The common name of Benzene-1,2-diol is

The solubility product of salt $\mathrm{B}_2 \mathrm{~A}$ is $3.2 \times 10^{-11}$ at 298 K . What is solubility of the salt at same temperature?

Identify the product formed when Hex-3-enenitrile is reduced with diisobutylaluminium hydride followed by acid hydrolysis?

Which of the following xenon compound has chlorine pentafluoride like structure?

Calculate cryoscopic constant of solvent if depression in freezing point of 0.18 m solution of nonvolatile solute is 0.2 K

What is the natural source of salicylic acid?

Calculate the number of unit cells in $1 \mathrm{~cm}^3$ of an element if unit cell edge length is $2.0 \times 10^{-8} \mathrm{~cm}$.

Identify the carbon atom numbered from $\mathrm{C}_1^{\prime}$ to $\mathrm{C}_5$ of monosaccharide unit of DNA nucleotide that lacks oxygen atom from -OH group.

What is the oxidation number of carbon in methanal?

Which from following is the most commonly used refrigerant Freon-12?

Which among the following salts turns red litmus blue in its aqueous solution?

Identify ' $B$ ' in the following sequence of reactions.

Acetic acid $\xrightarrow[\Delta]{\text { Thionyl chloride }} \mathrm{A} \xrightarrow{\text { Ammonia }} \mathrm{B}$

A container consists mixture of four gases as $5 \mathrm{~g} \mathrm{H}_2, 8 \mathrm{~g} \mathrm{He}, 50 \mathrm{~g} \mathrm{CO}_2$ and 20 g Ne at a certain temperature. Which of the following gases exerts minimum partial pressure?

Calculate the work done if 1 mole of certain gas compressed isothermally and reversibly at 300 K from initial pressure $x$ bar to final pressure $2 x$ bar $\left[\mathrm{R}=8.314 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right]$

Which from following compounds has lowest boiling point?

Calculate the radius of an atom of an element in pm if it forms bcc unit cell structure having edge length $4.3 \times 10^{-8} \mathrm{~cm}$.

Identify acidic amino acid from following list represented by three letter symbols.

What is the number of unpaired electrons in f orbitals of lutetium in its +3 oxidation state?

Which of the following elements has highest electronegativity?

A complex reaction takes place in following steps.

$$ \begin{aligned} & \mathrm{NO}_2 \mathrm{Cl}_{(\mathrm{g})} \longrightarrow \mathrm{NO}_{2(\mathrm{~g})}+\mathrm{Cl}_{(\mathrm{g})} \text { (slow) } \\ & \mathrm{NO}_2 \mathrm{Cl}_{(\mathrm{g})}+\mathrm{Cl}_{(\mathrm{g})} \longrightarrow \mathrm{NO}_{2(\mathrm{~g})}+\mathrm{Cl}_{2(\mathrm{~g})} \text { (fast) } \end{aligned} $$

Identify rate law equation for this reaction.

Which among the following has highest boiling point?

Which of the following is correct decreasing order of bond length regarding $\mathrm{N}_2, \mathrm{O}_2$ and $\mathrm{Cl}_2$ ?

Calculate the standard enthalpy change of following reaction.

$$ \begin{aligned} & \mathrm{CH}_{4(\mathrm{~s})}+2 \mathrm{O}_{2(\mathrm{~g})} \rightarrow \mathrm{CO}_{2(\mathrm{~g})}+2 \mathrm{H}_2 \mathrm{O}_{(\ell)} \\ & \text { if } \Delta_{\mathrm{f}} \mathrm{H}^{-}\left(\mathrm{CH}_4\right)=-75 \mathrm{~kJ} \mathrm{~mol}^{-1} \end{aligned} $$

$$ \Delta_{\mathrm{f}} \mathrm{H}^*\left(\mathrm{CO}_2\right)=-390 \mathrm{~kJ} \mathrm{~mol}^{-1} $$

$$ \Delta_{\mathrm{r}} \mathrm{H}^{\circ}\left(\mathrm{H}_2 \mathrm{O}\right)=-286 \mathrm{~kJ} \mathrm{~mol}^{-1} $$

What is reduction potential of hydrogen gas electrode when pure hydrogen gas is at I atmospheric pressure and platinum electrode is in contact with HCl solution of pH 1 at 298 K ?

Identify tertiary amine from following.

Which of the following aqueous solutions having same molality exhibits maximum boiling point elevation? (Assume complete dissociation)

Identify the monomers used in preparation of dacron.

Identify least stable species from following.

Which instrument is used for determination of particle size?

Identify ' $A$ ' in the following reaction.

$$ \begin{aligned} &\mathrm{A}+\text { chloromethane } \xrightarrow[\mathrm{AlCl}_3]{\text { Anhydrous }} \text { 2-chlorotoluene }+4 \text {-chlorotoluene } \end{aligned} $$

What is the average rate of reaction when change in concentration of product is 0.05 M in 20 seconds?

Identify the product ' $A$ ' in the following reaction, Anisole $\xrightarrow[398 \mathrm{~K}]{\mathrm{HI}} \mathrm{A}$ + Iodomethane

"Pairing of electrons in the orbitals belonging to the same subshell does not occur unless each orbital belonging to that subshell has got one electron each." This statement is known as

What is oxidation state of xenon in xenonmonooxytetrafluoride?

Calculate the mole fraction of pure liquid $B$ in solution if total vapour pressure of solution, vapour pressure of pure liquid A and vapour pressure of pure liquid B are 500 mm Hg , 400 mm Hg and 575 mm Hg respectively at given temperature.

What happens to the emf for the cell, ${ }^{-} \mathrm{Zn}_{(\mathrm{s})}\left|\mathrm{Zn}_{(1 \mathrm{M})}^{+2} \| \mathrm{Ag}^{+1}(1 \mathrm{M})\right| \mathrm{Ag}_{(\mathrm{s})}^{+}$if concentration of $\mathrm{Ag}^{+1}$ decreases to 0.1 M ?

The attractive interactions between cations and mobile electrons in metallic solid is called

Identify weak field ligand from following.

What is the value of spin only magnetic moment for $\mathrm{Cu}^{2+}$ in BM?

Identify role of glycerol in following reaction.

$$ 2 \mathrm{H}_2 \mathrm{O}_{2(\ell)} \xrightarrow{\text { glycerol }} 2 \mathrm{H}_2 \mathrm{O}_{(\ell)}+\mathrm{O}_{2(g)} $$

Which of the following is a Fittig reaction?

The slope of a graph $\log [A]_1$ versus ' $t$ ' for first order reaction is $-2.5 \times 10^{-3} \mathrm{~s}^{-1}$. Find rate constant of the reaction?

Identify the product formed in the following reaction.

$$ \mathrm{CH}_3 \mathrm{CH}_2 \mathrm{MgBr} \xrightarrow[\text { ii) dil. HCl }]{\text { i) Dry ice/ dry ether }} \text { Product } $$

What is pH of weak dibasic acid, that is $2 \%$ dissociated in its M/100 solution at 298 K ?

Which of the following net cell reaction takes place in a galvanic cell containing copper electrode and standard hydrogen electrode?

$$ \mathrm{E}^{o}\left(\mathrm{Cu}_{(\mathrm{aq})}^{+2} \mid \mathrm{Cu}_{(\mathrm{s})}\right)=+0.34 \mathrm{~V} $$

Identify neutral complex from following.

Which from following polymers is used to obtain surgical sutures?

Which of the following statement is a tautology?

Let $f(x)= \begin{cases}\frac{x^4-5 x^2+4}{|(x-1)(x-2)|} & , x \neq 1,2 \\ 6 & , x=1 \\ 12 & , x=2\end{cases}$

Then $\mathrm{f}(x)$ is continuous on the set

If $x$ and $y$ are sides of two squares such that $y=x-x^2$, then the rate of change of area of the second square with respect to that of the first square is

The acute angle between the line $4 x-2 y+13=0$ and the line which makes equal intercepts with the co-ordinate axes is

$$ \int\limits_0^1 x\left|x-\frac{1}{2}\right| \mathrm{d} x= $$

The function $\mathrm{f}(x)=[x(x-2)]^2$ is increasing in the set

If $p, q, r, s$ are statements, where, $\mathrm{p}: \mathrm{A}^2-\mathrm{B}^2=(\mathrm{A}-\mathrm{B})(\mathrm{A}+\mathrm{B}) ; \mathrm{A}, \mathrm{B}$ are matrices, $A B \neq B A$

q: $5 \leq 5$

r: ${ }^8 \mathrm{C}_1+{ }^8 \mathrm{C}_2+{ }^8 \mathrm{C}_3+\ldots \ldots \ldots . .+{ }^8 \mathrm{C}_8=256$

s: Maximum value of ${ }^8 \mathrm{C}_{\mathrm{r}}$ is 70 then the statement from the following having truth value true is ….

The minimum value of $a x+b y$ where $x y=c^2$ is

$$ \mathop {\lim }\limits_{x \to 0} \frac{\mathrm{e}^{x^2}-\cos 3 x}{\sin x \log (1+2 x)}= $$

$$ \int_0^{\frac{\pi}{2}} \frac{300 \sin x+100 \cos x}{\sin x+\cos x} d x=\ldots $$

If $A$ is a matrix of order 2 and $I$ is the identity matrix of order 2 such that $A^2-4 A+3 I=0$ then $(A+3 I)^{-1}=$

In a triangle $A B C$ with usual notations if $\angle A=30^{\circ}$, then the value of $\left(1+\frac{a}{c}+\frac{b}{c}\right)\left(1+\frac{c}{b}-\frac{a}{b}\right)=$

In a triangle PQR with usual notations, $\angle \mathrm{R}=\frac{\pi}{2}$. If $\tan \frac{\mathrm{P}}{2}$ and $\tan \frac{\mathrm{Q}}{2}$ are the roots of the equation $a x^2+b x+c=0(a \neq 0)$, then

If $\cot ^{-1}(\sqrt{\cos \alpha})-\tan ^{-1}(\sqrt{\cos \alpha})=x$, then the value of $\sin x$ is

Considering only the principal values of the inverse trigonometric functions, the value of $\tan \left(\sin ^{-1}\left(\frac{3}{5}\right)-2 \cos ^{-1}\left(\frac{2}{\sqrt{5}}\right)\right)$ is

If the area bounded by the curve $x^2=4 y, \mathrm{X}$-axis and the line $x=4$ is divided into equal areas by the line $x=\alpha$, then the value of $\alpha$ is …

If $p^3=q^4=r^6=t^7=s^2$, then $\log _t(p q r s)=\ldots \ldots$

The equation of the curve passing through the point $(0,2)$ given that the sum of the ordinate and abscissa of any point exceeds the slope of the tangent to the curve at that point by 5 is

Let z be the complex number such that $|z|+z=3+i$ where $i=\sqrt{-1}$, then $|z|=$

The solution of the differential equation $(1+x) \frac{\mathrm{d} y}{\mathrm{~d} x}-x y=1-x$ is

$$ \int \frac{\mathrm{d} x}{\sin ^2 x \cos ^2 x}= $$

If the angles $\mathrm{A}, \mathrm{B}$ and C of a triangle are in A.P. and if $\mathrm{a}, \mathrm{b}$ and c denote the length of the sides opposite to $\mathrm{A}, \mathrm{B}$ and C respectively, then the value of $\frac{a}{b} \sin 2 B+\frac{b}{a} \sin 2 A$ is

If the pair of lines $3 x^2-5 x y+\mathrm{p} y^2=0$ and $6 x^2-x y-5 y^2=0$ have one line common, then $\mathrm{p}=$

The number of ways in which 6 boys and 4 girls can be seated around a round table such that 2 special boys and a special girl never sit together is

The differential equation representing the family of parabolas having vertex at the origin and axis along the positive Y -axis is

$$ \int \frac{\mathrm{d} x}{x^{\frac{1}{2}}+x^{\frac{1}{3}}}=\mathrm{A} x^{\frac{1}{2}}+\mathrm{B} x^{\frac{1}{3}}+\mathrm{C} x^{\frac{1}{6}}+\mathrm{D} \log \left(x^{\frac{1}{6}}+1\right)+\mathrm{k} $$

(where k is the integration constant) then values of $\mathrm{A}, \mathrm{B}, \mathrm{C}$ and D are respectively,

The probability that a non leap year selected at random will contain 52 Saturdays or 53 Sundays is

The population of towns A and B increase at the rate proportional to their population present at that time. At the end of the year 1984, the population of both the towns was 20,000 . At the end of the year 1989, the population of town A was 25,000 and that of town B was 28,000 . The difference of populations of towns A and B at the end of 1994 was

The vectors $\bar{a}, \bar{b}$ and $\bar{c}$ are such that $|\overline{\mathrm{a}}|=2,|\overline{\mathrm{~b}}|=4,|\overline{\mathrm{c}}|=4$. If the projection of $\overline{\mathrm{b}}$ on $\overline{\mathrm{a}}$ is equal to projection of $\overline{\mathrm{c}}$ on $\overline{\mathrm{a}}$ and $\overline{\mathrm{b}}$ is perpendicular to $\overline{\mathrm{c}}$, then the value of $|\overline{\mathrm{a}}+\overline{\mathrm{b}}-\overline{\mathrm{c}}|$ is

Two tangents to the circle $x^2+y^2=4$ at the points A and B meet at $\mathrm{P}(-4,0)$. Then the area of quadrilateral PAOB, where ' $O$ ' is the origin is

The lines $\frac{6 x-6}{18}=\frac{y+1}{3}=\frac{z-1}{5} \quad$ and $\frac{3 x+6}{12}=\frac{y-1}{3}=\frac{z+1}{2}$ are $\ldots$

$$ \int x^2 \cos x d x= $$

A random variable $X$ has the following probability distribution :

$$ \begin{array}{|l|c|c|c|c|} \hline \mathrm{X}=x & 1 & 2 & 3 & 4 \\ \hline \mathrm{P}(\mathrm{X}=x) & 0.1 & 0.2 & 0.3 & 0.4 \\ \hline \end{array} $$

The mean and standard deviation of $X$ are respectively

The values of $x$ for which the angle between the vectors $\overline{\mathrm{a}}=2 x^2 \hat{\mathrm{i}}+4 x \hat{\mathrm{j}}+\hat{\mathrm{k}}$ and $\overline{\mathrm{b}}=7 \hat{\mathrm{i}}-2 \hat{\mathrm{j}}+x \hat{\mathrm{k}}$ is obtuse, are

If $\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}$ are three coplanar vectors such that $|\overline{\mathrm{a}}|=1,|\overline{\mathrm{~b}}|=2, \overline{\mathrm{~b}} \cdot \overline{\mathrm{c}}=8$ and the angle between $\overline{\mathrm{b}}$ and $\overline{\mathrm{c}}$ is $45^{\circ}$ then the value of $|\overline{\mathrm{a}} \times(\overline{\mathrm{b}} \times \overline{\mathrm{c}})|$ is

If $u=\log (\sqrt{x-1}-\sqrt{x+1})$ and $v=\sqrt{x+1}+\sqrt{x-1}$ then $\frac{d u}{d v}=\ldots$.

The line $\frac{x-1}{2}=\frac{y+2}{-1}=\frac{z}{1}$ intersects the XY plane and the YZ plane at points A and B respectively. The equation of line through the points A and B is

A fair $n$ faced die is rolled repeatedly until a number less than $n$ appears. If the mean of the number of tosses required is $\frac{n}{9}$, then $\mathrm{n}=($ where $\mathrm{n} \in \mathbb{N})$

A fair coin is tossed a fixed number of times. If the probability of getting 5 tails is same as the probability of getting 7 tails, then the probability of getting 3 tails is

In the above figure, P divides AC in the ratio $3: 4$ and Q divides BC in the ratio $4: 3$. Then M divides AQ in the ratio

The tangent to the ellipse $9 x^2+16 y^2=288$ making equal intercepts on the co-ordinate axes intersects the X -axis and the Y -axis in the points $A$ and $B$ respectively. Then $A(\triangle O A B)=$ (where O is origin)

The distance of the point $\mathrm{A}(3,-4,5)$ from the plane $2 x+5 y-6 z=16$ measured along the line $\frac{x}{2}=\frac{y}{1}=\frac{z}{-2}$ is

The direction cosines of a normal to the plane passing through $(4,2,3),(-1,4,2)$ and $(3,2,1)$ are …..

The unit vectors perpendicular to the plane determined by the points $\mathrm{A}(1,-1,2), \mathrm{B}(2,0,-1)$, $\mathrm{C}(0,2,1)$ is

The equation of the plane passing through the point $(1,1,1)$ and through the line of intersection of $x+2 y-z+1=0$ and $3 x-y-4 z+3=0$ is

A manufacturing company produces two items, A and B. Each toy should be processed by two machines, I and II. Machine I can be operated for maximum 10 hours 40 minutes. It takes 20 minutes for an item of A and 15 minutes for B. Machine II can be operated for a total time at 8 hours 20 minutes. It takes 5 minutes for an item A and 8 minutes for B . The profit per item of $A$ is $Rs 25$ and per item of $B$ is ₹ 18 . The formulation of an L.P.P. to maximize the profit (where $x$ is number of items A and $y$ is the number of item $B$ ) is

$$ \begin{array}{r}If\,\,\,\, y=\tan ^{-1}\left(\frac{1}{1+x+x^2}\right)+\tan ^{-1}\left(\frac{1}{x^2+3 x+3}\right) +\tan ^{-1}\left(\frac{1}{x^2+5 x+7}\right) \end{array} $$

then the value of $y^{\prime}(0)$ is

If $0 \leq x \leq \pi$ and $81^{\sin ^2 x}+81^{\cos ^2 x}=30$ Then $x$ takes the value

If $\mathrm{f}(x)=3 x^2+2 x \mathrm{f}^{\prime}(1)+\mathrm{f}^{\prime \prime}(2)$, then $\mathrm{f}(x)=\ldots \ldots .$.

The equation of the tangent to the curve $y=\mathrm{be}^{-x / \mathrm{a}}$ at the point where it crosses the Y axis is

The magnetic moment of electron due to orbital motion is proportional to ( $\mathrm{n}=$ principal quantum number)

A same torque is applied to a disc and a ring of equal mass and radii then

A capacitor of unknown capacity is connected across a battery of V volt. The charge stored in it is Q coulomb. When potential across the capacitor is reduced by $\mathrm{V}_1$ volt, the charge stored in it becomes $\mathrm{Q}_1$ coulomb. The potential V is

If p-n junction diode is forward biased, then

Two spherical black bodies have radii ' $R_1$ ' and ' $\mathrm{R}_2$ '. Their surface temperatures are ' $\mathrm{T}_1$ ' and ' $T_2$ '. If they radiate same power, then $\frac{R_2}{R_1}$ is

Lorentz magnetic force is acting on a particle of charge q moving with velocity $\vec{V}$ in a magnetic field $\vec{B}$. The work done by this force on the charged particle is

Graph shows the variation of fringe width ( X ) versus distance of the screen from the plane of the slits (D) in Young's double slit experiment. (keeping other parameters same, $d=$ distance between the slits). The wavelength of light used can be calculated as

The point charges $+\mathrm{q},-\mathrm{q},-\mathrm{q},+\mathrm{q},+\mathrm{Q}$ and -q are placed at the vertices of a regular hexagon ABCDEF as shown in figure. The electric field at the centre of hexagon ' $O$ ' due to the five charges at $\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}$ and F is twice the electric field at centre ' O ' due to charge +Q at E alone. The value of $Q$ is

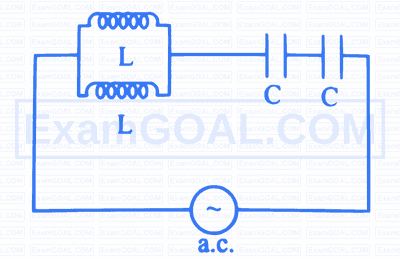
$$ \text { The frequency at resonance for the circuit is } $$

The work done in splitting a water drop of radius R into 64 droplets is ( $\mathrm{T}=$ surface tension of water)

Refractive index of a glass convex lens is 1.5 . The radius of curvature of each of the two surfaces of the lens is 40 cm . The ratio of the power of the lens when immersed in a liquid of refractive index 1.25 to that when placed in air is

A solid sphere at rests rolls down an inclined plane of vertical height $h$ without sliding. Its speed on reaching the bottom of plane is ( $\mathrm{g}=$ acceleration due to gravity)

A simple pendulum is suspended from ceiling of a lift when lift is at rest its period is ' T '. With what acceleration ' $a$ ' should lift be accelerated upward in order to reduce the period to ' $T$ '? (take ' g ' as acceleration due to gravity)

Five capacitors, each of capacitance ' $C$ ' are connected as shown in the figure. The ratio of equivalent capacitance between P and R and the equivalent capacitance between P and Q is

Let $E_c$ and $E_p$ represents kinetic energy of electron and photon respectively. If de-Broglie wavelength of a photon is twice the de-Broglie wavelength of an electron then $E_p / E_c$ is (speed of electron $=\mathrm{C} / 100$ where C is the velocity of light)

The fundamental frequency of an air column in a pipe closed at one end is 150 Hz . If the same pipe is open at both the end, the frequencies produced in Hz are

When the observer moves towards a stationary source with velocity $\mathrm{V}_1$, the apparent frequency of emitted note is $F_1$. When observer moves away from the source with velocity $\mathrm{V}_1$, the apparent frequency is $\mathrm{F}_2$. If V is the velocity of sound in air and $F_1 / F_2=2$ then $V / V_1$ is equal to

An ideal gas taken through a process ABCA as shown in figure. If the net heat supplied to gas in the cycle is 5 J , then the work done by the gas in process from C to A is

In Young's double slit experiment, in an interference pattern second minimum is observed exactly in front of one slit. The distance between the two coherent sources is ' $d$ ' and the distance between source and screen is ' $D$ '. The wavelength of light source used is

In an a.c. circuit containing $L, C, R$ in series the ratio of true power to apparent power is ( $\mathrm{Z}=$ impedance of the circuit and R is the resistance)

Two wires of equal lengths are bent in the form of a square and a circular loop. They are suspended in a uniform magnetic field and same current is passed through them. Torque experienced by

A calorimeter contains 10 g of water at $20^{\circ} \mathrm{C}$. The temperature fall to $15^{\circ} \mathrm{C}$ in 10 min . When calorimeter contains 20 g of water at $20^{\circ} \mathrm{C}$, it takes 15 min . for the temperature to become $15^{\circ} \mathrm{C}$. The water equivalent at the calorimeter is

Under isothermal conditions, two soap bubbles of radii $r_1$ and $r_2$ coalesce to form a big drop. The radius of the big drop is

The frequencies for series limit of Balmer and Paschen series are ' $\mathrm{V}_1$ ' and ' $\mathrm{V}_3$ ' respectively. If frequency of first line of Balmer series ' $\mathrm{V}_2$ ' then the relation between $V_1, V_2$ and $V_3$ is

Two cylinders A and B fitted with piston contain equal amount of an ideal diatomic gas at temperature T K. The piston of cylinder A is free to move while that of cylinder $B$ is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise of temperature of the gas in A is $\mathrm{dT}_{\mathrm{A}}$, then the rise in temperature of the gas in B is $\left(\gamma=\frac{C_p}{C_v}\right)$

In a certain 2 -inputs logic gate, when inputs $\mathrm{A}=0$ and $\mathrm{B}=0$, then output $\mathrm{C}=1$. And also when inputs $\mathrm{A}=0, \mathrm{~B}=1$, then again output $\mathrm{C}=1$. The gate must be

The vector sum of two forces $\vec{A}$ and $\vec{B}$ is perpendicular to their vector difference. Hence forces $\vec{A}$ and $\vec{B}$ are

In the following circuit, current through ACB if each resistance $\mathrm{R}=4 \Omega$ is

A particle is performing S.H.M. starting from extreme position. Graphical representation shows that between displacement and acceleration, there is a phase difference of

The plot of magnetic flux ' $\phi$ ' linked with the coil versus current ' I ' is as shown in figure for two inductors $\mathrm{L}_1$ and $\mathrm{L}_2$. The self inductance of

A musical instrument ' P ' produce sound waves of frequency ' $n$ ' and amplitude ' $A$ '. Another musical instrument ' $Q$ ' produces sound waves of frequency ' $\frac{\mathrm{n}}{4}$ ' The waves produced by ' P ' and ' $Q$ ' have equal energies. If the amplitude of waves produced by ' P ' is ' $\mathrm{A}_{\mathrm{p}}$ ', the amplitude of waves produced by ' $Q$ ' will be

The depth at which acceleration due to gravity becomes $\frac{g^{\prime}}{n}$ is ( $R=$ radius of earth, $\mathrm{g}=$ acceleration due to gravity) ( $\mathrm{n}=$ integer)

The polarising angle of transparent medium is ' $\theta$ '. Let the speed of light in the medium be ' v '. Then the relation between ' $\theta$ ' and ' $\mathbf{v}$ ' is [ $\mathrm{c}=$ velocity of light in air]

A black sphere has radius $R$ whose rate of radiation is E at temperature T . If radius is made R / 2 and temperature 3T, the rate of radiation will be

For a transistor, $\alpha_{\mathrm{dc}}$ and $\beta_{\mathrm{dc}}$ are the current ratios, then the value of $\frac{\beta_{\mathrm{dc}}-\alpha_{\mathrm{dc}}}{\alpha_{\mathrm{dc}} \times \beta_{\mathrm{dc}}}$

Two coils P and Q are kept near each other. When no current flows through coil P and current increases in coil Q at the rate $10 \mathrm{~A} / \mathrm{s}$, the emf in coil P is 12 mV . When coil Q carries no current and current of 1.5 A flows through coil P , the magnetic flux linked with the coil Q in mWb is

A mass ' M ' is suspended by a rope from a rigid support at point ' P ' as shown in figure. Another rope is tied at end ' Q ' and pulled horizontally with a force ' $F$ '. If the rope makes an angle ' $\theta$ ' with vertical then the tension in the string ' PQ ' is

A mass ' $M$ ' attached to a horizontal spring executes S.H.M. of amplitude $A_1$. When the mass M passes through its mean position, then a smaller mass ' $m$ ' is placed over it and both of them move together with amplitude $\mathrm{A}_2$. The ratio $\left(\frac{A_1}{A_2}\right)$ is

The function of a dielectric in a capacitor is

When one end of the capillary is dipped in water, the height of water column is ' $h$ '. The upward force of 108 dyne due to surface tension is balanced by the force due to the weight of water column. The inner circumference of the capillary is (surface tension of water $=7.2 \times 10^{-2} \mathrm{~N} / \mathrm{m}$ )

The graph shows the variation of photocurrent with anode potential for four different radiations. Let $\mathrm{I}_{\mathrm{a}}, \mathrm{I}_{\mathrm{b}}, \mathrm{I}_{\mathrm{c}}$ and $\mathrm{I}_{\mathrm{d}}$ are intensities and $\mathrm{f}_{\mathrm{a}}, \mathrm{f}_{\mathrm{b}}, \mathrm{f}_{\mathrm{c}}$ and $\mathrm{f}_{\mathrm{d}}$ be the frequencies for the curves $\mathrm{a}, \mathrm{b}, \mathrm{c}$ and d respectively, then

A car moving at a speed ' V ' is stopped in a certain distance when the breaks produce a deceleration ' $a$ '. If the speed of the car is ' $n v$ ', what must be the deceleration of the car to stop it in the same distance and in the same time?

A radio active element has rate of disintegration 8000 disintegrations per minute at a particular instant. After four minutes it becomes 2000 disintegrations per minute. The decay constant per minute is

The closed and open organ pipes have same length. When they are vibrating simultaneously in first overtone, they produce four beats. The length of open pipe is made half and that of the closed pipe is made two times the original. Now the number of beats produced if the two pipes are vibrating in their fundamental modes simultaneously is

In series LCR circuit R $=18 \Omega$ and impedance is $30 \Omega$. An rms voltage 210 V is applied across the circuit. The true power consumed in AC circuit is nearly

In the thermodynamic processes, which of the following statements is NOT true?

In an experiment four quantities $\mathrm{p}, \mathrm{q}, \mathrm{r}$ and s are measured with percentage $3 \%, 2 \%, 3 \%$ and $1 \%$ respectively. Quantity ' $A$ ' is calculated as follows

$\mathrm{A}=\frac{\mathrm{pq}^2}{\mathrm{r}^2 \mathrm{~s}^4}$, the percentage error in ' A ' is

A man standing on a turn-table is rotating at a certain angular frequency with his arms outstretched. He suddenly folds his arms. If his moment of inertia with folded arms is $75 \%$ of that with outstretched arms, then his rotational kinetic energy will

Kirchhoff's voltage law and current law are based (respectively) on the conservation of