In a time series forecasting model, the demand for five time periods was $$10, 13,$$ $$15,$$ $$18$$ and $$22.$$ A linear regression fit resulted in an equation $$F = 6.9 + 2.9$$ $$t$$ where $$F$$ is the forecast for period $$t$$. The sum of absolute deviations for the five data is

In a single server infinite population queuing model, arrivals follow a Poisson distribution with mean $$\lambda = 4$$ per hour. The service times are exponential with mean service time equal to $$12$$ minutes. The expected length of the queue will be

Solve the following linear programming problem by simplex method

$$\eqalign{ & Maximize\,\,\,\,\,\,4{x_1} + 6{x_2} + {x_3} \cr & Subject\,\,to\,\,\,\,\,\,2{x_1} - {x_2} + 3{x_3}\, \le 5 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1},{x_2},{x_3} \ge 0 \cr} $$

$$(a)$$$$\,\,\,\,\,\,\,$$ What is the solution to the above problem?

$$(b)$$$$\,\,\,\,\,\,\,$$ Add the constant $${x_2} \le 2$$ to the simplex table of part $$(a)$$ and find the solution.

Given below is a basic feasible solution to a transportation problem with three supply points $$(A,B,C)$$ and three demand points $$(P, Q, R)$$ that minimizes cost of transportation in the standard tabular format.

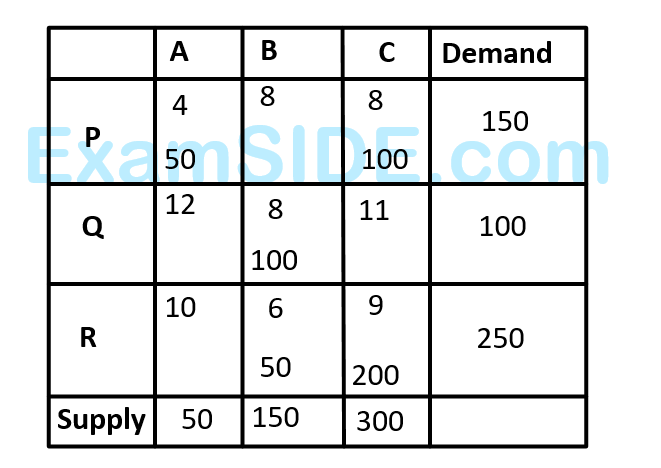
$$(a)$$$$\,\,\,\,\,\,\,\,$$ Compute the cost corresponding to the present solution
$$(b)$$$$\,\,\,\,\,\,\,\,$$ It is optimal?
$$(c)$$$$\,\,\,\,\,\,\,\,$$ Does an alternate optimum exist ?