In a single server infinite population queuing model, arrivals follow a Poisson distribution with mean $$\lambda = 4$$ per hour. The service times are exponential with mean service time equal to $$12$$ minutes. The expected length of the queue will be

Solve the following linear programming problem by simplex method

$$\eqalign{ & Maximize\,\,\,\,\,\,4{x_1} + 6{x_2} + {x_3} \cr & Subject\,\,to\,\,\,\,\,\,2{x_1} - {x_2} + 3{x_3}\, \le 5 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1},{x_2},{x_3} \ge 0 \cr} $$

$$(a)$$$$\,\,\,\,\,\,\,$$ What is the solution to the above problem?

$$(b)$$$$\,\,\,\,\,\,\,$$ Add the constant $${x_2} \le 2$$ to the simplex table of part $$(a)$$ and find the solution.

Given below is a basic feasible solution to a transportation problem with three supply points $$(A,B,C)$$ and three demand points $$(P, Q, R)$$ that minimizes cost of transportation in the standard tabular format.

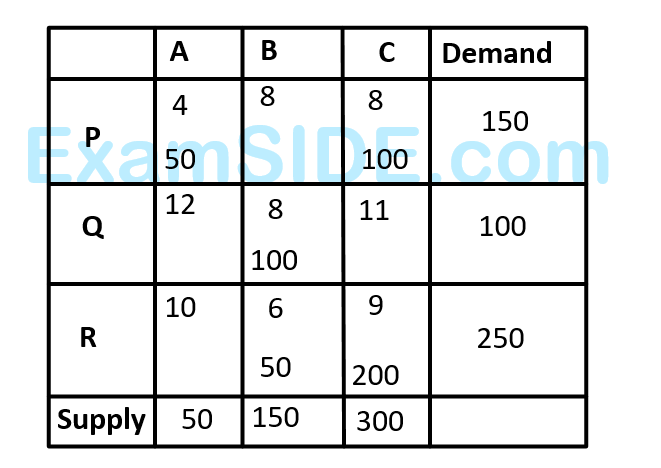
$$(a)$$$$\,\,\,\,\,\,\,\,$$ Compute the cost corresponding to the present solution
$$(b)$$$$\,\,\,\,\,\,\,\,$$ It is optimal?
$$(c)$$$$\,\,\,\,\,\,\,\,$$ Does an alternate optimum exist ?

The forecasts for a product for the next three months are given as $$750,850$$ and $$1000$$ units. The number of regular time days and overtime days available are $$22,18,$$ $$22$$ and $$4,$$ $$4,5$$ respectively. With the existing number of employees, the company can produce $$38$$ units per day. To meet the high demand in the third month, the company decides to hire people to increase the daily production to $$45$$ units.

The following costs are given :
Cost of regular time production $$=$$ Rs. $$20$$ per unit
Cost of overtime production $$=$$ Rs. $$25$$ Per unit
Cost of hiring $$=$$ $$200{L^2}$$
where $$'L'$$ is the increase in daily capacity

Inventory $$=$$ Rs. $$10$$ per unit per month (based on average inventory)
Shortage (back-ordering cost) $$=$$ Rs. $$20$$ per unit per month

The beginning inventory is $$100$$ units. The company decides to produce $$800,$$ $$700$$ and $$900$$ units respectively in the three months. Compute the cost of the production plan.