1
GATE ME 2016 Set 1
Numerical
+2
-0
An infinitely long furnace of $$0.5m \times 0.4m$$ cross-section is shown in the figure below. Consider all surfaces of the furnace to be black. The top and bottom walls are maintained at temperature $${T_1} = {T_3} = {927^ \circ }C,$$
while the side walls are at temperature $${T_2} = {T_4} = {527^ \circ }C.$$
The view factor, $${F_{1 - 2}}$$ is $$0.26.$$ The net radiation heat loss or gain on side $$1$$ is_________ $$W/m.$$ Stefan-Boltzman constant $$ = \,5.67 \times {10^{ - 8}}$$ $$W/{m^2}$$-$${K^4}$$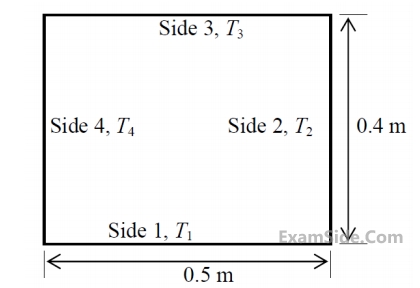
while the side walls are at temperature $${T_2} = {T_4} = {527^ \circ }C.$$
The view factor, $${F_{1 - 2}}$$ is $$0.26.$$ The net radiation heat loss or gain on side $$1$$ is_________ $$W/m.$$ Stefan-Boltzman constant $$ = \,5.67 \times {10^{ - 8}}$$ $$W/{m^2}$$-$${K^4}$$

Your input ____
2
GATE ME 2016 Set 1
Numerical
+2
-0
A fluid (Prandtl number, $$Pr=1$$) at $$500$$ $$K$$ flows over a flat plate of $$1.5$$ $$m$$ length, maintained at $$300$$ $$K.$$ The velocity of the fluid is $$10\,\,m/s.$$ Assuming kinematic viscosity, $$v = 30 \times {10^{ - 6}}\,\,{m^2}/s,$$ the thermal boundary layer thickness (in $$mm$$) at $$0.5$$ $$m$$ from the leading edge is _________.
Your input ____
3
GATE ME 2016 Set 1
Numerical
+2
-0
The annual demand for an item is $$10,000$$ units. The unit cost is Rs. $$100$$ and inventory carrying charges are $$14.4\% $$ of the unit cost per annum. The cost of one procurement is Rs. $$2000.$$ The time between two consecutive orders to meet the above demand is _______ month(s).
Your input ____
4
GATE ME 2016 Set 1
MCQ (Single Correct Answer)
+2
-0.6
Maximize $$\,\,\,\,Z = 15{x_1} + 20{x_2}$$
Subject to
$$\eqalign{ & 12{x_1} + 4{x_2} \ge 36 \cr & 12{x_1} - 6{x_2} \le 24 \cr & \,\,\,\,\,\,\,\,\,{x_1},\,\,{x_2} \ge 0 \cr} $$
Subject to
$$\eqalign{ & 12{x_1} + 4{x_2} \ge 36 \cr & 12{x_1} - 6{x_2} \le 24 \cr & \,\,\,\,\,\,\,\,\,{x_1},\,\,{x_2} \ge 0 \cr} $$
The above linear programming problem has
Paper analysis
Total Questions
Engineering Mathematics
8
Engineering Mechanics
4
Fluid Mechanics
4
Heat Transfer
4
Industrial Engineering
2
Machine Design
1
Production Engineering
10
Strength of Materials
7
Theory of Machines
3
Thermodynamics
4
Turbo Machinery
1
More papers of GATE ME
GATE ME 2025
GATE ME 2024
GATE ME 2023
GATE ME 2022 Set 2
GATE ME 2022 Set 1
GATE ME 2020 Set 2
GATE ME 2020 Set 1
GATE ME 2019 Set 1
GATE ME 2019 Set 2
GATE ME 2018 Set 2
GATE ME 2018 Set 1
GATE ME 2017 Set 2
GATE ME 2017 Set 1
GATE ME 2016 Set 1
GATE ME 2016 Set 3
GATE ME 2016 Set 2
GATE ME 2015 Set 2
GATE ME 2015 Set 1
GATE ME 2015 Set 3
GATE ME 2014 Set 1
GATE ME 2014 Set 4
GATE ME 2014 Set 2
GATE ME 2014 Set 3
GATE ME 2014 Set
GATE ME 2014
GATE ME 2013
GATE ME 2012
GATE ME 2011
GATE ME 2010
GATE ME 2009
GATE ME 2008
GATE ME 2007
GATE ME 2006
GATE ME 2005
GATE ME 2004
GATE ME 2003
GATE ME 2002
GATE ME 2001
GATE ME 2000
GATE ME 1999
GATE ME 1998
GATE ME 1997
GATE ME 1996
GATE ME 1995
GATE ME 1994
GATE ME 1993
GATE ME 1992
GATE ME 1991
GATE ME 1990
GATE ME 1989
GATE ME 1988
GATE ME 1987
GATE ME
Papers
2025
2024
2023
2014
2013
2012
2011
2010
2009
2008
2007
2006
2005
2004
2003
2002
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
1991
1990
1989
1988
1987