A $$5$$-stage pipelined processor has Instruction Fetch $$(IF),$$ Instruction Decode $$(ID),$$ Operand Fetch $$(OF),$$ Perform Operation $$(PO)$$ and Write Operand $$(WO)$$ stages. The $$IF, ID, OF$$ and $$WO$$ stages take $$1$$ clock cycle each for any instruction. The $$PO$$ stage takes $$1$$ clock cycle for $$ADD$$ and $$SUB$$ instructions, $$3$$ clock cycles for $$MUL$$ instruction, and $$6$$ clock cycles for $$DIV$$ instruction respectively. Operand forwarding is used in the pipeline. What is the number of clock cycles needed to execute the following sequence of instructions?

A hash table of length 10 uses open addressing with hash function h(k)=k mod 10, and linear probing. After inserting 6 values into an empty hash table, the table is as shown below 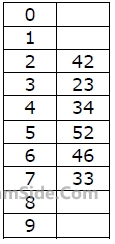How many different insertion sequences of the key values using the same hash function and linear probing will result in the hash table shown above?

The following C function takes a simply-linked list as input argument. It modifies the list by moving the last element to the front of the list and returns the modified list. Some part of the code is left blank.

typedef struct node { 
    int value; 
    struct node *next; 
} Node;
 
Node *move_to_front(Node *head) { 
     Node *p, *q; 
     if ((head = = NULL: || (head->next = = NULL)) return head; 
     q = NULL; p = head; 
     while (p-> next !=NULL) { 
       q=P; 
       p=p->next; 
     } 
     return head; 
} 

Choose the correct alternative to replace the blank line.

Consider a complete undirected graph with vertex set {0,1,2,3,4}. Entry W_ij in the matrix W below is the weight of the edge {i, j} $$$W = \left( {\matrix{ 0 & 1 & 8 & 1 & 4 \cr 1 & 0 & {12} & 4 & 9 \cr 8 & {12} & 0 & 7 & 3 \cr 1 & 4 & 7 & 0 & 2 \cr 4 & 9 & 3 & 2 & 0 \cr } } \right)$$$ What is the minimum possible weight of a spanning tree T in this graph such that vertex 0 is a leaf node in the tree T?