COMEDK 2025 Evening Shift | COMEDK Paper Questions with Solutions

COMEDK 2025 Evening Shift

Paper was held on Sat, May 10, 2025 12:00 PM

Chemistry

An aqueous solution of an electrolyte $\mathrm{A}_3 \mathrm{~B}$ is prepared by dissolving 0.5625 g in 750 ml of water and is found to be $80 \%$ ionised. If $\mathrm{K}_{\mathrm{b}}$ for water is $0.52 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$, calculate the boiling point of the solution at 1.0 atm pressure.

Arrange the complex ions in the increasing order of their magnetic moments

A. $\left[\mathrm{Fe}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right]^{2+}$
B. $\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{4-}$
C. $\left[\mathrm{Fe}(\mathrm{CN})_6\right]^{3-}$
D. $\left[\mathrm{FeF}_6\right]^{3-}$

When the temperature of a reaction $\mathrm{A}+\mathrm{B} \rightarrow \mathrm{C}$ is increased from 300 K to 310 K the rate constant increases by $12 \%$. What is the Activation energy of the reaction?

The first electron gain enthalpy of oxygen is $-141 \mathrm{~kJ} \mathrm{~mol}^{-1}$, its second electron gain enthalpy is :

Two moles of an ideal gas at 1 bar pressure and 298 K is expanded into vacuum to double the volume. The work done is :

The order of a reaction $\mathrm{W}+\mathrm{X} ---- \rightarrow \mathrm{Y}+\mathrm{Z}$ with respect to W is 3 and with respect to X is 1. If the concentrations of both W and X are tripled, the rate of reaction will increase by _________ times.

Identify the correct statement.

For the cell reaction $4 \mathrm{Br}^{-}+\mathrm{O}_2+4 \mathrm{H}^{+} \rightarrow 2 \mathrm{Br}_2+2 \mathrm{H}_2 \mathrm{O}$ at 298 K , the $\mathrm{E}^0$ cell $=0.16 \mathrm{~V}$. What would be the $\mathrm{K}_{\mathrm{c}}$ (Equilibrium constant) value if the reverse reaction were to take place?

The bond angles in the following molecules decreases in the order. $\mathrm{BF}_3, \mathrm{NH}_3, \mathrm{PF}_3$ and $\mathrm{XeF}_2$

Two statements, one Assertion and the other Reason, are given. Choose the correct option.

Assertion : During the electrolysis of aqueous $\mathrm{NaCl}, \mathrm{Cl}_2$ is liberated at the anode in preference to $\mathrm{O}_2$ and water gets reduced to $\mathrm{H}_2$ at cathode.

Reason : The reaction at Anode with lower oxidation potential is not preferred due to over potential of Oxygen.

An aqueous solution of volume V ml contains a non-volatile solute of unknown mass $W_B \mathrm{~g}$ and molar mass $M_B \mathrm{~g} / \mathrm{mol}$. If the Osmotic pressure of the solution is 1.013 bar, which one of the following is the mathematical expression to be used to calculate $W_B$ ?

The ratio of $\mathrm{N}_2$ and $\mathrm{O}_2$ gases in the atmosphere is $4: 1$. The ratio of the mole fractions of the dissolved gases $\mathrm{N}_2$ : $\mathrm{O}_2$ in rain water will be approximately ........ (At $293 \mathrm{~K}, \mathrm{~K}_{\mathrm{H}}$ for Nitrogen and Oxygen in kbar units are 76.48 and 34.86 respectively.)

Identify the correct coefficients (a), (b), (c) and (d) in the following equations

i) $\quad \mathrm{xMnO}_4^{--}+$(a) $\mathrm{SO}_3{ }^{2-}+$ (b) $\mathrm{H}^{+} \cdots \longrightarrow \mathrm{xMn}^{2+}+$ (a) $\mathrm{SO}_4{ }^{2-}+$ (c) $\mathrm{H}_2 \mathrm{O}$

ii) (c) $\mathrm{S}_2 \mathrm{O}_3{ }^{2-}+$ (d) $\mathrm{MnO}_4^{-}+\mathrm{H}_2 \mathrm{O} \cdots \rightarrow$ (d) $\mathrm{MnO}_2+$ (b) $\mathrm{SO}_4{ }^{2-}+\mathrm{xOH}^{-}$

The decomposition of $\mathrm{PH}_3$ follows first order kinetics. The time required for $3 / 4^{\text {th }}$ of $\mathrm{PH}_3$ to decompose is 75.76 s . Calculate the fraction of original amount of $\mathrm{PH}_3$ which will remain after 2.0 minutes.

An example of disproportionation reaction is :

Identify the Alkane (molecular formula $\mathrm{C}_8 \mathrm{H}_{18}$ ) which yields only a single monochloride on Chlorination in the presence of sunlight.

For a reaction,

$$A+B \rightleftharpoons 2 C$$

1.0 mole of $A, 1.5$ mole of $B$ and 0.5 mole of $C$ were taken in a 1 L vessel. At equilibrium, the concentration of $C$ was $1.0 \mathrm{~mol} \mathrm{~L}^{-1}$. The equilibrium constant for the reaction is $x / 15$. The value of ' $x$ ' is:

The correct order of reactivity of halogens with alkanes is :

Match the reactions given in Column I with the major product formed given in Column II.

S.No.	Reactions	S.No.	Major product formed
A.		P.
B.		Q.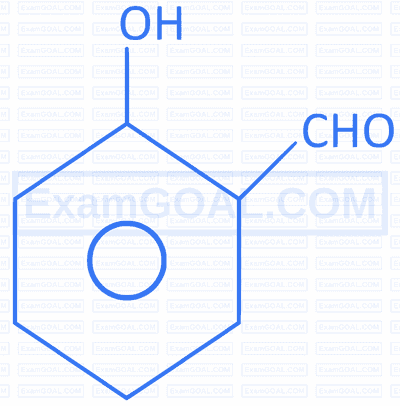
C.		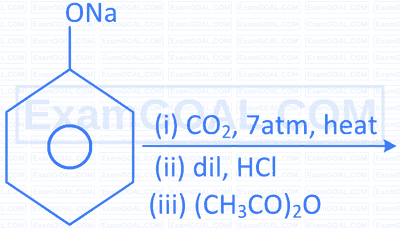R.
D.		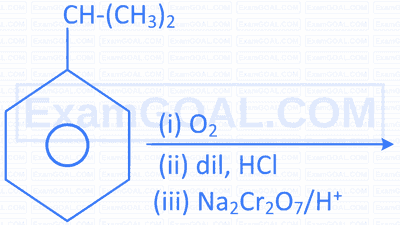S.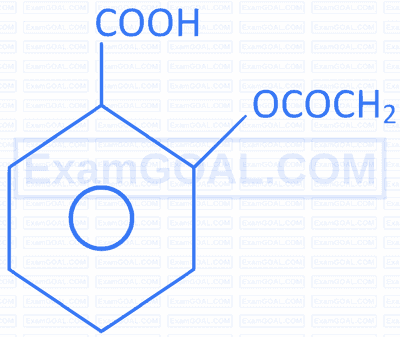

The number of grams of bromine that will completely react with 5 g of pentene is : [Atomic mass of $\mathrm{Br}=80 \mathrm{u}$ ]

Two statements, one Assertion and the other Reason are given. Choose the right option.

Assertion : Insulin is called a protein whereas Glycyl alanine is not called a protein

Reason : A polypeptide with amino acid residue less than 100 can also be called as a protein if it has a well-defined conformation of a protein.

Choose the correct metal/ ion from the brackets which -------------------------

A. has chemical reactivity similar to that of the first few members of the Lanthanoids $(\mathrm{Zn}, \mathrm{Ca}, \mathrm{Fe}, \mathrm{Cu})$.

B. has stable $4 \mathrm{f}^7$ electronic configuration, but acts as a strong reducing agent and converts to $\mathrm{M}^{3+}$ state. $\left(\mathrm{Eu}^{2+}, \mathrm{Ce}^{2+}, \mathrm{Pr}^{2+}, \mathrm{Dy}^{2+}\right)$

C. is a colorless ion $\left(\mathrm{Tm}^{3+}, \mathrm{Lu}^{3+}, \mathrm{Gd}^{3+}, \mathrm{Sm}^{3+}\right)$.

D. shows stable +2 oxidation state and is diamagnetic ( $\mathrm{Ce}, \mathrm{Sm}, \mathrm{Ho}, \mathrm{Yb}$ )

Which of the following alkene on reductive ozonolysis gives ketones only as the product

The oxidation number of potassium in $\mathrm{K}_2 \mathrm{O}, \mathrm{K}_2 \mathrm{O}_2$ and $\mathrm{KO}_2$ respectively are:

For a cell $2 \mathrm{M}_{(\mathrm{S})}+\mathrm{O}_2(\mathrm{~g})+4 \mathrm{H}^{+} \rightarrow 2 \mathrm{M}^{2+}(\mathrm{aq})+2 \mathrm{H}_2 \mathrm{O}_{(\mathrm{l})}$ the $\mathrm{E}^0$ cell $=+1.67 \mathrm{~V}$. When $\left[\mathrm{M}^{2+}\right]$ is $1.0 \times 10^{-3} \mathrm{M}$ and $\mathrm{p}\left(\mathrm{O}_2\right)$ is 0.1 atm , the EMF of the cell becomes +1.57 V . Calculate the pH of the electrochemical cell.

What would be the major product formed in the reaction?

When $0.1 \mathrm{~mol} \mathrm{~L}^{-1}$ of KCl was filled in a Conductivity cell the resistance was 80 ohms at 298 K . (Conductivity of 0.1 M KCl at 298 K is $1.29 \mathrm{~S} \mathrm{~m}^{-1}$. The same cell when filled with an unknown electrolyte of concentration 0.025 M , had a resistance of 92 ohms. What is the Molar conductivity of the electrolyte at the given concentration?

An optically active compound $[\mathrm{X}]$ (Molecular formula $\mathrm{C}_8 \mathrm{H}_{11} \mathrm{~N}$ ) reacts with $\mathrm{CHCl}_3$ / Ethanolic KOH on heating to form an isocyanide. On reaction with $\mathrm{NaNO}_2 / \mathrm{HCl}$, it yields an alcohol with liberation of $\mathrm{N}_2$. Identify the compound $[\mathrm{X}]$.

Choose the correct statement from the options given

The number of electrons with azimuthal quantum numbers $l=1$ and $l=2$ for Cr in the ground state electronic configurations are respectively. [Given: $\mathrm{Cr}(\mathrm{Z}=24)$ ]

The ratio of the difference between the radii of $3^{\text {rd }}$ and $4^{\text {th }}$ orbits of the $\mathrm{He}^{+}$and those of $\mathrm{Li}^{2+}$ is:

Consider the reaction

$$\mathrm{Fe}_2 \mathrm{O}_3(\mathrm{~s})+3 \mathrm{CO}(\mathrm{~g}) \rightleftharpoons 2 \mathrm{Fe}(\mathrm{l})+3 \mathrm{CQ}_2(\mathrm{~g})$$

In accordance with Le-Chatlier's principle, which of the following will not disturbs the equilibrium?

The electronic configuration of the element with atomic number 78 is :

Identify the final product $[\mathrm{Y}]$ in the following reaction.

Choose the incorrect statement.

Find the correct matches.

A.	$\mathrm{Cr}_2 \mathrm{O}_7^{2-}$	P.	is predominantly a basic compound.
B.	$\mathrm{FeCr}_2 \mathrm{O}_4$	Q.	is predominantly a acidic compound
C.	$\mathrm{CrO}_3$	R.	forms yellow chromate on reaction with $\mathrm{Na}_2 \mathrm{CO}_3$ in air.
D.	$\mathrm{CrO}$	S.	is interconvertible with $\mathrm{MO}_4^{2-}$ depending on the pH of the medium.

Which of the following compounds has electrons symmetrically distributed in both $\mathrm{t}_{2 \mathrm{~g}}$ and $\mathrm{e}_{\mathrm{g}}$ orbitals?

Identify the two incorrect electrochemical reactions shown as taking place in the given cells at the respective electrodes.

Cell	Electrode	Reaction
Lead-Storage Cell	Cathode	$\mathrm{Pb}+2 \mathrm{SO}_4{ }^{2-}+4 \mathrm{H}^{+}+2 \mathrm{e}^{-} \rightarrow \mathrm{PbSO}_4+2 \mathrm{H}_2 \mathrm{O}+\mathrm{SO}_2$
Leclanche Cell	Cathode	$\mathrm{MnO}_2+\mathrm{NH}_4^{+}+2 \mathrm{e}^{-} \rightarrow \mathrm{MnO}+\mathrm{OH}+\mathrm{NH}_3$
Mercury Cell	Anode	$\mathrm{Zn} / \mathrm{Hg}+2 \mathrm{OH}^{-} \rightarrow \mathrm{ZnO}(\mathrm{s})+\mathrm{H}_2 \mathrm{O}+2 \mathrm{e}^{-}$
Fuel Cell	Cathode	$\mathrm{O}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}+4 \mathrm{e}^{-} \rightarrow 4 \mathrm{OH}^{-}$

Choose the correct statement.

Consider the following reaction

$$\text { Propyne }+\mathrm{CH}_3 \mathrm{MgBr} \xrightarrow{\text { dry ether }} \mathbf{X}$$

Identify ' X ' from the following.

Match the IUPAC names in Column II with the correct structures given in Column I.

		IUPAC name
A	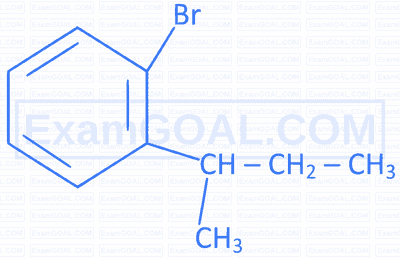P	1-Bromomethyl-3-(2,2-dimethylpropyl)benzene
B	Q	1-Bromo-4-(1-methylethyl)benzene
C	R	1-Bromo-2-(1-methylpropyl)benzene
D	S	1-Bromo-4-(2-methylpropyl)benzene

An organic compound $[\mathrm{X}]$ (Molecular formula $\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_2$ ) reacts with dil. $\mathrm{H}_2 \mathrm{SO}_4$ to form an alcohol [B] and a carboxylic acid [C]. Reaction of compound $[\mathrm{B}]$ with Jones reagent yielded compound $[\mathrm{C}]$. When compound $[\mathrm{C}]$ was heated with $\mathrm{P}_2 \mathrm{O}_5$ an Anhydride was formed. Compound $[\mathrm{X}]$ is ------------- --

In the decomposition of limestone to lime, the values of $\Delta H^o$ and $\Delta S^o$ are $+179.1 \mathrm{~kJ} \mathrm{~mol}^{-1}$ and $160.2 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}$. Calculate the temperature above which conversion of limestone to lime will be spontaneous, if values of $\Delta H^o$ and $\Delta S^o$ remain unchanged with temperature. [Assuming pressure 1 bar ]

The mole fraction of an unknown solute in 1560 g of Benzene is 0.5 . What is the molality of the solution? (M. M of Benzene:78 amu)

Which of the coordination compounds [(i) to (v)] are used for the following processes :

A: Electroplating

B: Removal of excess copper from human body

C: Estimation of hardness of water

(i) DMG (ii) $\mathrm{Na}_2 \mathrm{EDTA}$ (iii) Cis-platin (iv) D-penicillamine (v) $\mathrm{K}\left[\mathrm{Au}(\mathrm{CN})_2\right]$

Identify the type of reaction:

Identify X, Y and Z formed in the reaction:

Which of the following is a water soluble vitamin?

At 300 K the vapour pressure of an ideal solution containing 1.0 mole each of volatile liquids X and Y is 1000 mm . Keeping the temperature constant, when 2.0 moles of liquid X is added to the solution, its vapour pressure increases by 200 mm . Calculate the vapour pressure of X and Y in their pure state

The maximum polarity and dipole moment among the following is :

During a chemical reaction $\mathrm{X} \rightarrow \mathrm{Y}$, the rates of reaction starting with initial concentrations of X as $4.0 \times 10^{-3} \mathrm{M}$ and $2.0 \times 10^{-3} \mathrm{M}$ are $4.8 \times 10^{-4} \mathrm{~mol} \mathrm{~L}^{-1} / \mathrm{s}$ and $1.2 \times 10^{-4} \mathrm{~mol} \mathrm{~L}^{-1} / \mathrm{s}$ respectively. What is the order of reaction with respect to X ?

Identify the Carbonyl compound which will not be formed when hydration of Alkynes is carried out with dil. $\mathrm{H}_2 \mathrm{SO}_4 / \mathrm{Hg}^{2+}$ at 333 K .

Acetone, Butanal, Ethanal, Butanone.

Choose the incorrect statement from the following.

Identify $[\mathrm{X}]$ used in the given reaction.

$[\mathrm{X}]+$ Copper $/ 573 \mathrm{~K} \rightarrow[\mathrm{Y}]$

$[\mathrm{Y}] \xrightarrow[\text { (ii) } \mathrm{H}_2 \mathrm{O} / \mathrm{H}^{+}]{\text {(i) } \mathrm{CH}_3 \mathrm{MgBr}}$ Tert.butyl alcohol. (major product)

Which one of the following is the product $(\mathrm{Z})$ formed at the end of the given reaction:

$$\begin{aligned} & \text { Propan-1-ol }+\mathrm{SOCl}_2 \rightarrow[\mathrm{X}] \\ & {[\mathrm{X}]+\mathrm{HC} \equiv \mathrm{C}-\mathrm{Na} \rightarrow[\mathrm{Y}]} \\ & {[\mathrm{Y}]+\mathrm{H}_2 \mathrm{SO}_4 / \mathrm{HgSO}_4, 330 \mathrm{~K} \rightarrow[\mathrm{Z}]} \end{aligned}$$

Two statements, one Assertion and the other Reason are given. Identify the correct option

Assertion : Primary and secondary amides on treatment with $\mathrm{Br}_2$ and alcoholic NaOH yield primary and secondary amines respectively and the reaction involves stepping down the series.

Reason : The reaction occurs due to the migration of alkyl group from Carbonyl carbon atom to the Nitrogen atom with elimination of carbonyl group as the carbonate salt.

The enthalpies of combustion of $\mathrm{H}_2, \mathrm{C}$ (graphite) and $\mathrm{C}_2 \mathrm{H}_6(\mathrm{~g})$ are $-286.0,-394.0$ and $-1560.0 \mathrm{~kJ} \mathrm{~mol}^{-1}$ at $25^{\circ} \mathrm{C}$ and 1 atm pressure. The enthalpy of formation of ethane is :

Which of the following is the most stable free radical?

What are the intermediates formed during the reactions $A$ and $B$ ?

A. Reimer-Tiemann reaction.

B. Dehydration of alcohols in the slow rate determining step.

Arrange the following in the increasing order of their covalent character.

$\mathrm{CaF}_2 ; \mathrm{CaCl}_2 ; \mathrm{CaBr}_2 ; \mathrm{CaI}_2$

Mathematics

A function $f$ from the set of natural numbers to integers defined by

$$f(n)=\left\{\begin{array}{l} \frac{n-1}{2}, \quad \text { when } n \text { is odd } \\ -\frac{n}{2}, \quad \text { when } n \text { is even } \end{array} \quad\right. \text { is }$$

The value of $\frac{\sin ^2 20^{\circ}+\cos ^4 20^{\circ}}{\sin ^4 20^{\circ}+\cos ^2 20^{\circ}}$ is :

$$\int \frac{\sin 2 x}{(1+\sin x)(2+\sin x)} d x=a \log |1+\sin x|-b \log |2+\sin x|+c$$ then the value of $a$ and $b$ is ----------------

The solution for the following system of inequalities $3 x-7<5+x$ and $11-5 x \leq 1$ on a real number line is

Kiran purchased 3 pencils, 2 notebooks and one pen for ₹41. From the same shop Manasa purchased 2 pencils, one notebook and 2 pens for ₹ 29 , while Shreya purchased 3 pencils, 2 notebooks and 2 pens for ₹ 44. The above situation can be represented in matrix form as $A X=B$. Then $|\operatorname{adj} A|$ is equal to

The area of a triangle formed by the lines joining the vertex of the parabola $x^2=\lambda y$ to the ends of its latus rectum is 18 sq units then the value of $\lambda$ is

If $X=\left[\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right]$ and $Y=\left[\begin{array}{cc}0 & 1 \\ -1 & 0\end{array}\right]$ and $B=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{array}\right]$ then $B$ equals :

Two numbers are selected at random from integers 1 to 9 . If their sum is even, what is the probability that both the numbers are odd?

If the standard deviation of $0,1,2,3 \cdots\cdots\cdots9$ is ' $k$ ' then the standard deviation of $10,11,12,13, \cdots\cdots\cdots\cdots19$ will be :

If $A=\left[\begin{array}{ll}a & b \\ b & a\end{array}\right]$ and $(A I)^2=\left[\begin{array}{ll}\alpha & \beta \\ \beta & \alpha\end{array}\right]$ where I is the identity matrix then

Let $f(x)=x \sqrt{4 a x-x^2}, a>0$ then $f^{\prime}(x)$ at $x=2 a$ is :

The angle between two lines is $45^{\circ}$ and slope of one line is $\frac{1}{4}$ then which is the possible value of the slope of the other line.

Given $Z=80 x+120 y$, subject to constraints are $x+3 y \leq 30 ; 3 x+4 y \leq 60 ; x \geq 0 ; y \geq 0$. P is one of the corner points of the feasible region for the given Linear Programming Problem. Then the coordinate of $P$ is

If $\sin x+\sin ^2 x=1$ then $\cos ^8 x+2 \cos ^6 x+\cos ^4 x$ is equal to :

$\int_0^1 x(1-x)^{99} d x=$

Value of the determinant of a matrix $A$ of order $3 \times 3$ is 7 . Then the value of the determinant formed by the cofactors of matrix A is

The relationship between a and b for the continuous function

$f(x)=\left\{\begin{array}{ll}a x+1, & \text { if } x \leq 3 \\ b x+3, & \text { if } x>3\end{array}\right.$ at $x=3$ is

If the function $f(x)=\mu \sin x+\frac{1}{3} \sin 3 x$ has its derivative equal to zero at $x=\frac{\pi}{3}$, then the value of ' $\mu$ ' is

A man is moving away from a tower 41.6 m high at a rate of $2 \mathrm{~m} / \mathrm{s}$. If the eyelevel of the man is 1.6 m above the ground, then the rate at which the angle of elevation of the top of the tower changes, when he is at a distance of 30 m from the foot of the tower is :

$\sin ^{-1}(x-1)+\cos ^{-1}(x-3)+\tan ^{-1}\left(\frac{x}{2-x^2}\right)=\cos ^{-1} k+\pi$, then the value of ' $k$ ' is

Given that $z$ is a real number and $z=\frac{\lambda+4 i}{1+\lambda i}$ where $\lambda \in R$, then the possible value of $\lambda$ is :

If $z=\left(\frac{\sqrt{3}}{2}+\frac{i}{2}\right)^5+\left(\frac{\sqrt{3}}{2}-\frac{i}{2}\right)^5$, then

The solution of the differential equation: $x \cos y d y=\left(x e^x \log x+e^x\right) d x$ is

Area of the region bounded by the curve $y=\cos x$ between $x=-\frac{\pi}{2}$ and $x=\pi$ is ------------------

If a quadratic function in $x$ has the value 19 when $x=1$ and has a maximum value 20 when $x=2$, then the function is

If A and B are two events such that $P(\bar{A})=0.3, P(B)=0.4, P(A \cap \bar{B})=0.5$, then find the value of $P(B / A \cup \bar{B})$

If $\lim\limits_{x \rightarrow 1} \frac{x^4-1}{x-1}=\lim\limits_{x \rightarrow k} \frac{x^3-k^3}{x^2-k^2}$, then the value of K is :

$\int\left(e^{x \log _e 6}\right) e^x d x=\phi(x)+c$ then $\phi(x)=$

The number of solutions of $\frac{d y}{d x}=\frac{y+1}{x-1}$, when $y(1)=2$ is :

Evaluate: $\lim _\limits{x \rightarrow 0} \frac{\sqrt[3]{1+x}-\sqrt[3]{1-x}}{x}$

A geometric progression consists of an even number of terms. If the sum of all the terms is five times the sum of the terms occupying the odd places, then the common ratio of the geometric progression is

Find the function ' $f$ ' which satisfies the equation $\frac{d f}{d x}=2 f$, given that $f(0)=e^3$

In a game, a man wins ₹ 1000 if he gets an even number greater than or equal to 4 on a fair dice and loses ₹ 200 for getting any other number on the dice. If he decides to throw the dice until he wins or maximum of three times, then his expected gain/loss in (₹) is -----------

The number of words that can be formed with the letters of the word 'DEFINITE' if two vowels are together and the other two are also together but separated from the first two is

The relation $R=\{(1,1),(2,2),(3,3)\}$ on the set $\{1,2,3\}$ is

If the length of the diagonal of a square is increasing at the rate of $0.1 \mathrm{~cm} / \mathrm{sec}$. What is the rate of increase of its area when the side is $\frac{15}{\sqrt{2}} \mathrm{~cm}$ ?

Two finite sets have $m$ and $n$ elements. The total number of proper subsets of the first set is 119 more than the total number of subsets of the second set. Find the value of $m-n$

Given that n number of arithmetic means are inserted between two pairs of numbers $a, 2 b$ and $2 a, b$; where $a, b \in R$. If the $m^{\text {th }}$ means in the two cases are the same, then the ratio $a: b$ is equal to

$\int\limits_{-2}^2 \frac{|x-3|}{x-3} d x=$

If $x=a\left[\left\{\cos t+\frac{1}{2} \log \left(\tan ^2 \frac{t}{2}\right)\right\}\right]$ and $y=a \sin t$ then $\frac{d y}{d x}=$

If the area under the curve $y=\sqrt{a^2-x^2}$ included between the lines $x=0$ and $x=a$ is 4 sq units. Then the value of ' $a$ ' is

The function $y=\frac{\log x}{x^3}$ is strictly increasing function for

If $P=\{5 m: m \in N\}$ and $Q=\left\{5^m: m \in N\right\}$, where $N$ is set of natural numbers, then

The image of a point $P(3,5,3)$ in the line $\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}$ is $P^{\prime}(a, b, c)$. Then $a+b+c=$

If $\vec{a}$ and $\vec{b}$ are two vectors such that $\vec{a} \cdot \vec{b}=|\vec{a} \times \vec{b}|$ then the angle between $\vec{a}$ and $\vec{b}$ is

How many natural numbers are there between 100 and 1000 such that at least one of their digits is $6 ?$

For any vector $\vec{p}$, the value of $\left[2\left\{|\vec{p} \times \hat{\imath}|^2+|\vec{p} \times \hat{\jmath}|^2+|\vec{p} \times \hat{k}|^2\right\}\right]$ is

$\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{1}{1+\sqrt{\tan x}} d x=$

A pot contains 5 red and 2 green balls. A ball is drawn at random from this pot. If a drawn ball is green, then a red ball is added to the pot. If a drawn ball is red, then a green ball is added to the pot, while the original ball drawn is not replaced in the pot. Now a second ball is drawn at random from the pot, what is the probability that the second ball drawn is a red ball?

If $A=\left[\begin{array}{ccc}4 & \lambda & -3 \\ 0 & 2 & 5 \\ 1 & 1 & 3\end{array}\right]$ then $A^{-1}$ exists if :

The value of $\tan \left\{\cos ^{-1}\left(\frac{\sqrt{2}}{2}\right)-\frac{\pi}{2}\right\}$ is

If the line $(3 x+14 y+7)+k(5 x+7 y+6)=0$ is perpendicular to $x$-axis then the value of ' $k$ ' is

A straight line makes positive intercepts on the coordinate axes whose sum is 5 . If the line passes through the point $P(-3,4)$ then the equation of a line is

If the foci of the ellipse $\frac{x^2}{16}+\frac{y^2}{b^2}=1$ and the foci of the hyperbola $\frac{x^2}{144}-\frac{y^2}{81}=\frac{1}{25}$ coincide, then the value of $b^2$ is

The equation of a line passing through origin with direction angles $\frac{2 \pi}{3}, \frac{\pi}{4}, \frac{\pi}{3}$ is

Two lines $\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{4}$ and $\frac{x-3}{1}=\frac{y-k}{2}=\frac{z}{1}$ intersect at a point. Then the value of ' $k$ ' is

Solve the following differential equation $\cos ^2 x \frac{d y}{d x}+y=\tan x$, given that $y(0)=1$. Hence find $y\left(\frac{\pi}{4}\right)$

If $\tan \alpha=\frac{1}{7}$ and $\sin \beta=\frac{1}{\sqrt{10}}, \quad 0<\alpha, \beta<\frac{\pi}{2}$ then $2 \beta$ is equal to

An unbiased die is tossed twice. What is the probability of getting a 4,5 or 6 on the first toss and a $1,2,3$ or 4 on the second toss?

If $y=x+e^x$ then $\frac{d^2 x}{d y^2}=$

Physics

The interference pattern is obtained with two coherent light sources of intensity ratio $9: 1$. The ratio of $\frac{I_{\operatorname{MAX}}+I_{\operatorname{MIN}}}{I_{\operatorname{MAX}}-I_{\operatorname{MIN}}}$ is $\frac{\alpha}{\beta}$. The values of $\alpha$ and $\beta$ are:

If the mass numbers of two nuclei are in the ratio $5: 2$ and their diameters are in ratio $2: 6$. Then their nuclear densities will be in the ratio

Which of the following is correct in the case of the Bohr model of atoms?

A. Predicts continuous emission spectra for all atoms

B. Assumes that the angular momentum of electrons is quantised

C. Predicts same emission spectrum for singly ionised neon atom and hydrogen atom

D. Predicts same emission spectrum for singly ionised neon atom and singly ionised helium atom

The zener voltage in the circuit shown is $\mathrm{V}_{\mathrm{Z}}=20 \mathrm{~V}$. The load resistance $\mathrm{R}_{\mathrm{L}}=5 \mathrm{k} \Omega$ and the resistance $\mathrm{R}_{\mathrm{S}}=10 \mathrm{k} \Omega$. If the input voltage is $\mathrm{V} \mathrm{s}=100 \mathrm{~V}$, then the current through the zener diode in milliampere is:

The unit of universal gravitational constant is :

In the normal adjustment of an astronomical telescope, the objective and eyepiece are 36 cm apart. If the magnifying power of the telescope is 8 , find the focal lengths of the objective and eyepiece.

A rectangular coil of 250 turns has an average area of $20 \mathrm{~cm} \times 15 \mathrm{~cm}$. The coil rotates with a speed of 60 cycles per second in a uniform magnetic field of $2 \times 10^{-2} \mathrm{~T}$ about an axis perpendicular to the field. The peak value of the induced emf is:

A beam of incident parallel light falls on a diverging lens of focal length 20 cm in magnitude. If a converging lens of focal length 15 cm in magnitude is placed at a distance of 10 cm to the right of the diverging lens on the other side, then, the final image formed is:

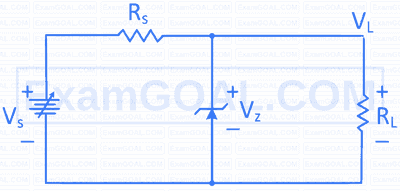
The total number of degrees of freedom associated with $2 \mathrm{~cm}^3$ of Nitrogen gas at normal temperature and pressure is:

[Given Avogadro number as ' N ' ]

A bob of a simple pendulum has a mass of 4 g and a charge of $20 \mu \mathrm{C}$. If it is at rest in a uniform horizontal electric field of intensity $1000 \mathrm{Vm}^{-1}$, the angle that the pendulum makes with the vertical at equilibrium is:

Three charges, $Q,-q$ and $2 q$ are placed at the vertices of a right-angled isosceles triangle. What is the value of $q$ for the net electrostatic energy of the configuration to be zero?

The minimum energy required by a hydrogen atom in ground state to emit radiation in Paschen series is nearly:

An object of height $h$ is placed midway between $f$ and $2 f$ in front of a biconvex lens. A real inverted image is captured on a screen placed a little beyond 2 f on the other side of the lens. If the whole arrangement is immersed in water without disturbing the object, lens and the screen positions, then the new image formed will be

A power transmission line feeds input power at 2200 V to a step-down transformer with its primary windings having 2000 turns. The output power is delivered at 220 V by the transformer. If the current in the primary of the transformer is 2 A and its efficiency is $80 \%$, the output current would be:

Two physical quantities having the same dimensional formula $\left[\mathrm{M}^1 \mathrm{~L}^{-1} \mathrm{~T}^{-2}\right]$ are

The stopping potential when a metal surface is illuminated by light of wavelength $\lambda$ is 15 V . The stopping potential when the same surface is illuminated by light of wavelength $4 \lambda$ is 3 V . The ratio of threshold wavelength to the initial incident wavelength $\lambda$ is:

A wire of negligible mass having uniform area of cross section ' A ' and young modulus ' Y ' is used to suspend a point mass ' m '. The point mass executes simple harmonic motion in a vertical plane with a period ' T ', then the length of the wire is :

Applying a constant torque the speed of a flywheel is increased from 1800 rpm to 2400 rpm in 10 seconds. The number of revolutions made by the flywheel during this time is:

A short bar magnet placed with its axis at $45^{\circ}$ with an external field of $400 \times 10^{-4} \mathrm{~T}$ experiences a torque of 0.024 Nm . If a solenoid of cross-sectional area $10^{-4} \mathrm{~m}^2$ and 500 turns replaces the short bar magnet such that they have the same magnetic moment, then the current flowing through the solenoid is:

If the distance between the Sun and Earth is doubled, then the duration of the year on earth will be :

[Given actual duration of the year $=\mathbf{T}$ ]

The rms velocity of the gas molecule at $327^{\circ} \mathrm{C}$ is same as the rms velocity of the oxygen molecules at $27^{\circ} \mathrm{C}$. If the molecular weight of oxygen is 32 then the molecular weight of the given gas molecule is:

Select the correct statement from the following: The position of the centre of mass of a system :

A particle of mass 3 g and charge $60 \mu \mathrm{C}$ is released from rest in a uniform electric field of intensity $10^5 N C^{-1}$. If the value of kinetic energy attained by the particle after moving through a distance of 2 cm is $m \times 10^{-2} J$, then the value of m is:

A network of capacitors is as shown below. If the voltage supply is 100 V , find the energy stored in the $6 \mu \mathrm{~F}$ capacitor.

$C_1=3 \mu F, C_2=6 \mu F, C_3=3 \mu F$ and $C_4=4 \mu F$

A body of mass 10 kg is moving up on an inclined plane of $30^{\circ}$ with an acceleration $2 \mathrm{~ms}^{-2}$. Find the force required, if the coefficient of friction between the object and the plane surface is $\frac{\sqrt{3}}{6}$, [given $g=10 \mathrm{~ms}^{-2}$ ].

A galvanometer having a resistance of $50 \Omega$ is shunted by a wire of resistance $10 \Omega$. If the total current is 2 A , the current passing through the shunt is:

The power dissipated across the $16 \Omega$ resistor in the circuit is 2 watts. The power dissipated in watt units across the $4 \Omega$ resistor is:

Select the graph which represents the motion of a particle along a straight line with uniform acceleration.

A metal rod of susceptibility 799 is subjected to a magnetising field of $2000 \mathrm{Am}^{-1}$. The permeability of the material of the rod is: (Given $\mu_0=4 \pi \times 10^{-7} \mathrm{TmA}^{-1}$ )

A given volume of gas at NTP is allowed to expand 6 times of its original volume, first under isothermal condition and then under adiabatic condition. Which of the given statement is correct? [Given $\frac{c_p}{c_v}=\gamma=1.4$ ]

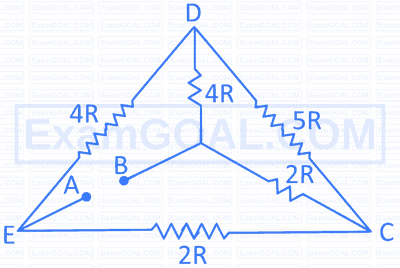
The net resistance between the points A and B in the circuit given below is:

The wavelength of a monochromatic light which is used in single slit diffraction is 800 nm . The width of the single slit for which the first minimum appears at $\theta=45^{\circ}$ on the screen will be:

A plane electromagnetic wave with frequency 40 MHz travels in free space. At a particular point in space and time, the magnetic field is $2 \times 10^{-8} T$. What will be the electric field at this point?

A series LCR circuit having $\mathrm{R}=44 \Omega, \mathrm{~L}=2 \mathrm{H}$ and $\mathrm{C}=25 \mu \mathrm{~F}$ is connected to a variable frequency of 220 V . What is the average power transferred to the circuit in one complete cycle if the frequency of supply equals the natural frequency of the circuit?

Momentum of a body is increased to three times its original value. By what percentage will its kinetic energy change?

What is the dc component of the output voltage if a sinusoidal signal of 33 V peak voltage is the input of a half wave diode rectifier circuit?

Radium having mass number 200 and binding energy per nucleon 5.6 MeV , splits into two fragments Cadmium of mass number 112 and Hassium of mass number 108. If the binding energy per nucleon for Cadmium and Hassium is approximately 8.0 MeV , then the energy $Q$ released per fission will be:

In a particular case X , a certain length of insulated copper wire is bent to form double loops of equal radii. In another case Y the same copper wire is bent to form three loops of equal radii. If the same steady current is passed through the copper wire in both the cases, the ratio of magnetic field at the centre in the case X to that in case Y is:

The fundamental frequency of sound produced in an open pipe of length $\mathbf{L}_1$ is same as the frequency of the $3^{\text {rd }}$ harmonic of the sound produced in the closed pipe of length $\mathbf{L}_2$ Then the ratio of $\frac{L_1}{L_2}$ is :

Select the correct statement from the following:

A straight wire of mass 250 g and length 2.5 m carries a current of 4 A . It can be suspended in mid air by a uniform horizontal magnetic field of magnitude:

Select the correct statement from the following:

A boy is running along a straight horizontal road with a constant speed $5 \mathrm{~ms}^{-1}$. While running he throws a stone with a velocity $30 \mathrm{~ms}^{-1}$ at an angle $60^{\circ}$ with the horizontal. Then the time of flight of the stone is: (Given $g=10 \mathrm{~ms}^{-2}$ )

In a pure inductive circuit, a sinusoidal voltage $V(t)=200 \sin 250 t$ is applied to a pure inductance of $\mathrm{L}=0.02 \mathrm{H}$. The current through the coil is:

In to a vessel containing pure water a clean glass tube of radius $3.6 \times 10^{-4} \mathrm{~m}$ is held vertically with 12 cm of the tube above the water level. Now the capillary tube is moved down in to the water so that only 2 cm of its length is above the water surface. Angle of contact $\Theta$ at this position is (given surface tension of water $=7.2 \times 10^{-2} \mathrm{Nm}^{-1}$ and $g=10 \mathrm{~ms}^{-2}$ )

A point marked on a ring of radius 2 cm is in contact with a horizontal plane. Now the ring is rolled forward half a revolution along the positive X - direction. Then the angle made by the displacement vector of the point with the X - axis is:

The instantaneous values of alternating current and voltages in a circuit are $\mathrm{I}=\frac{3}{\sqrt{2}} \sin (200 \pi t)$ ampere and $\mathrm{V}=\frac{3}{\sqrt{2}} \sin \left(200 \pi t+\frac{\pi}{6}\right)$ volt. What is the average power consumed in the circuit in watt ?

The velocity - mass graph of body with constant linear momentum is represented by the graph:

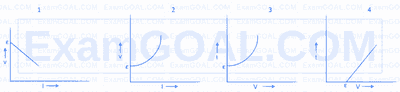
A student measures the terminal potential difference $V$ of a cell of emf $\varepsilon$ and internal resistance $r$ as a function of the current I flowing through it. Which of the following graphs will give the values of emf $\varepsilon$ and internal resistance $r$ ?

Young's double slit experiment is first done in air and then in a medium of refractive index $\mu$. If the 7 th dark fringe in the medium lies where the 4 th bright fringe is in air, then the value of $\mu$ is :

When ${ }^{10} \mathrm{~B}_5$ nuclei are bombarded by neutrons, one of the resultant nuclei is ${ }^7 \mathrm{Li}_3$. Then the emitted particle will be:

The resistance of a heating element is found to be $120 \Omega$ at room temperature which is $20^{\circ} \mathrm{C}$. If the temperature coefficient of the material of the resistor is $1.6 \times 10^{-4} C^{-1}$ and the resistance is found to be $160 \Omega$, the temperature of the element is:

A plot of kinetic energy of emitted photoelectrons from a metal versus the frequency of incident radiation gives a straight line, the intercept of which

A. Depends on the nature of the metal used

B. Depends on the intensity of radiation

C. Depends both on the intensity and the nature of metal used

D. Is a constant and is same for all metals which is independent of the intensity of Incident radiation

A plano-convex lens made of refractive index 1.5 and having radius of curvature $\mathrm{R}=4 \mathrm{~cm}$ fits exactly into a planoconcave lens made of refractive index 1.3 and having the same radius of curvature $R=4 \mathrm{~cm}$ such that their plane surfaces are parallel to each other. The focal length of the combination is :

The rate of heat conduction in the given two metal rods having the same length is found to be the same when the temperature difference between the ends is kept $30^{\circ} \mathrm{C}$ If the area of cross section of the first rod is $8 \times 10^{-2} \mathrm{~m}^2$ then what will be area of cross section of the second rod? [ Given that the ratio of the thermal conductivity of the first rod to that of the second rod is $1: 4$ ]

A current carrying closed loop in the form of a right isosceles triangle XYZ is placed in a uniform magnetic field $B$ acting along $X Y$ of the loop. If the magnetic force on the arm $Y Z$ is $\sqrt{2} F$, then the force on the arm $X Z$ is:

A capacitor of capacitance $4 \mu \mathrm{~F}$ is charged to a potential of 24 V and then connected in parallel to an uncharged capacitor of capacitance $6 \mu \mathrm{~F}$. The final potential difference across each capacitor will be:

A uniformly charged conducting sphere of 0.2 m diameter has a surface charge density of $70 \mu \mathrm{Cm}^{-2}$. The electric flux leaving the surface of the sphere is:

An intrinsic semiconductor has equal concentrations of hole and electron which is equal to $4 \times 10^8 \mathrm{~m}^{-3}$. During its conversion to extrinsic semiconductor, concentration of hole increases to $8 \times 10^{10} \mathrm{~m}^{-3}$. The new electron concentration is:

Two electric dipoles of dipole moments $3.9 \times 10^{-30} \mathrm{Cm}$ and $5.2 \times 10^{-30} \mathrm{Cm}$ are placed in two different uniform electric fields of strengths $16 \times 10^4 \mathrm{NC}^{-1}$ and $4 \times 10^4 \mathrm{NC}^{-1}$ respectively. What is the ratio of maximum torque experienced by the electric dipoles?