The chemical formula of Lucas reagent is

Alkyl halides undergoing S_N2 reaction do inverse

X and Y in the following reactions are

For the reaction, H$$_2$$(g) + I$$_2$$(g) $$\rightleftharpoons$$ 2HI(g) the position of equilibrium can be shifted to the right by

Which of the following are not path functions?

I. H $$-$$ TS

II. W

III. q

IV. q + W

The system that forms maximum boiling azeotropes is

KMnO$$_4$$ acts as an oxidising agent in acidic medium. The number of moles of KMnO$$_4$$ that will be required to react with one mole of oxalate ions (to form CO$$_2$$) in acidic solution is

What can be A and B in the following reaction?

Which of the following is a false statement?

Which of the following molecules does not exhibit dipole moment?

(i) CCl$$_4$$ (ii) CO$$_2$$ (iii) NH$$_3$$ (iv) CHCl$$_3$$ (v) H$$_2$$O (vi) CH$$_3$$$$-$$O$$-$$CH$$_3$$

Which of the following is highly basic?

The relation between work done in reversible and irreversible process is

What is the function platelets?

The monosaccharides of maltose is

Which of the following does not affect solubility of a gas in liquid?

A newly prepared radioactive nuclide has a decay constant of 6.93 s$$^{-1}$$. What is the half-life of the nuclide?

The essential amino acids are

(i) Leucine (ii) Glutamic acid (iii) Asparagine (iv) Valine

correct option is

Increasing order of bond order of oxygen and its ions is

Minimum number of nodes are present in

pH of 10$$^{-3}$$ M solution of KOH is

Which of the product is not possible in Wurtz reaction?

On treatment of glucose with bromine water the product formed is

Which among the following forms minimum boiling azeotropes?

(i) Heptane + Octane

(ii) Water + Nitric acid

(iii) Ethanol + Water

(iv) Acetone + Carbon dioxide

Which of the following statement is incorrect about activation energy?

The P-O bond order in PO$$_4^{3-}$$ is

$$\mathrm{O^{2-},F^-,Mg^{2+},Al^{3+},O_2,F_2}$$. How many of the species given above isoelectronic?

The equilibrium constant, $$K_C$$ for $$3C_2H_2(g) \rightleftharpoons C_6H_6(g)$$ is 4 L$$^2$$mol$$^{-2}$$. If the equilibrium concentration of benzene is 0.5 mol$$^{-1}$$ than what is the value of concentration of ethylene?

Identify the product formed in the given reaction.

Which of the following gas readily de-colourises the acidified KMnO$$_4$$ solution?

What will be the emf of the following cell at 25$$^\circ$$C?

Fe/Fe$$^{2+}$$ (0.001 M) | | H$$^+$$ (0.01 M) | H$$_2$$(g) (1 Bar) | Pt(s)

$$E_{(F{e^{2+}} /Fe)}^o = - 0.44$$ V; $$E_{({H^ + }/{H_2})}^o = - 0.00$$ V

Which of the following vitamin is responsible for Beri-Beri disease?

Find the product formed for the given reaction.

$$\mathrm{{C_6}{H_5}CHO + {H_3}C - C{H_2} - CHO\buildrel {Dil.\,NaOH/\Delta } \over \longrightarrow}$$

In which of the following changes, entropy decreases?

Which among the following will not liberate nitrogen on reaction with nitrous acid?

The complex which does not show optical isomerism is

The solution which have lowest freezing point is

Calculate the molar conductance of 0.025 M aqueous solution of calcium chloride at 25$$^\circ$$C. The specific conductance of calcium chloride is 12.04 $$\times$$ 10$$^{-2}$$ Sm$$^{-1}$$

For the reaction 2N$$_2$$O$$_5$$ $$\to$$ 4NO$$_2$$ + O$$_2$$.

If initial pressure is 100 atm and rate constant $$k$$ is 3.38 $$\times$$ 10$$^{-5}$$ s$$^{-1}$$. after 20 min the final pressure of N$$_2$$O$$_5$$ will be

The difference between heat capacity at constant pressure and heat capacity at constant volume is

Which of the following compound does not exists?

The major product in the given reaction is

The spectrum of He$$^+$$ is similar to

The Paschen series of hydrogen spectrum lies in which region?

The oxidation state of nickel in [Ni(CO$$_4$$)] is

The value of $${3^{{{\log }_4}5}} - {5^{{{\log }_4}3}}$$ is

If the tangent to the curve $$xy + ax + by = 0$$ at (1, 1) is inclined at an angle $${\tan ^{ - 1}}2$$ with X-axis, then

If $$\mathop {\lim }\limits_{x \to 0} {{(1 + {a^3}) + 8{e^{1/x}}} \over {1 + (1 - {b^3}){e^{1/x}}}} = 2$$, then

If two circles $${(x - 1)^2} + {(y - 3)^2} = {r^2}$$ and $${x^2} + {y^2} - 8x + 2y + 8 = 0$$ intersect in two distinct points, then

The approximate value of $$(0.007)^{1/3}$$ is

the circle $${x^2} + {y^2} + 4x - 7y + 12 = 0$$ cuts an intercept on Y-axis of length

Let $$f(x) = a - {(x - 3)^{8/9}}$$, then maxima of $$f(x)$$ is

If the derivative of the function $$f(x) = \left\{ {\matrix{ {b{x^2} + ax + 4;} & {x \ge - 1} \cr {a{x^2} + b;} & {x < - 1} \cr } } \right.$$ is everywhere continuous, then

If $$\mathop {\lim }\limits_{x \to \infty } {\left( {1 + {a \over x} + {b \over {{x^2}}}} \right)^{2x}} = {e^2}$$, then

$$S\equiv x^2+y^2+2x+3y+1=0$$ and $$S'\equiv x^2+y^2+4x+3y+2=0$$ are two circles. The point $$(-3,-2)$$ lies

The probability of choosing randomly a number c from the set {1, 2, 3, ... 9} such that the quadratic equation $$x^2+4x+c=0$$ has real roots, is

Shade the feasible region for the inequations $$6x+4y\le120, 3x+10y\le180,x,y\ge0$$ in a rough figure.

The maximum of Z is where, $$Z=4x+2y$$ subject to constraints $$4x+2y\ge46,x+3y\le24$$ and $$x,y\ge0$$ is

If for any 2 $$\times$$ 2 square matrix A,

A (adj A) = $$\left[ {\matrix{ 8 & 0 \cr 0 & 8 \cr } } \right]$$, then find the value of det (A).

If $$A = \left[ {\matrix{ a & 0 & 0 \cr 0 & a & 0 \cr 0 & 0 & a \cr } } \right]$$, then $$|A||adj\,A|$$ is equal to

If $$A = \left[ {\matrix{ {2 - k} & 2 \cr 1 & {3 - k} \cr } } \right]$$ is a singular matrix, then the value of $$5k - {k^2}$$ is

If $$\theta$$ be the angle between the vectors $$a = 2\widehat i + 2\widehat j - \widehat k$$ and $$b = 6\widehat i - 3\widehat j + 2\widehat k$$, then

If x, y and z are non-zero real numbers and $$a = x\widehat i + 2\widehat j,b = y\widehat j + 3\widehat k$$ and $$c = x\widehat i + y\widehat j + z\widehat k$$ are such that $$a \times b = z\widehat i - 3\widehat j + \widehat k$$, then [a b c] is equal to

Maximum value of $$z=12x+3y$$, subject to constraints $$x\ge0,y\ge0,x+y\ge5$$ and $$3x+y\le9$$ is

If $$\mathbf{p}=\hat{i}+\hat{j}, \mathbf{q}=4 \hat{k}-\hat{j}$$ and $$\mathbf{r}=\hat{i}+\hat{k}$$, then the unit vector in the direction of $$3 p+q-2 r$$ is

The line $$\frac{x-3}{4}=\frac{y-4}{5}=\frac{z-5}{6}$$ is parallel to the plane

$$\int \frac{1}{x \sqrt{a x-x^2}} d x$$ is

$$\int \frac{3^x}{\sqrt{1-9^x}} d x$$ is equal to

$$\int\limits_{ - {\pi \over 2}}^{{\pi \over 2}} {\cos x\,dx} $$

The angle between the lines $${{x + 4} \over 3} = {{y - 1} \over 5} = {{z + 3} \over 4}$$ and $${{x + 1} \over 1} = {{y - 4} \over 1} = {{z - 5} \over 2}$$ is

The point of intersection of the lines $${{x - 1} \over 1} = {{y - 1} \over 2} = {{z - 2} \over 3}$$ and $${{x -5} \over 2} = {{y - 2} \over 1} = z$$ is

Five persons A, B, C, D and E are in queue of a shop. The probability that A and B are always together is

If the probability for A to fail in an examination is 0.2 and that for B is 0.3, then the probability that either A or B fail is

Three vertices are chosen randomly from the seven vertices of a regular 7-sided polygon. The probability that they form the vertices of an isosceles triangle is

If A, B and C are three mutually exclusive and exhaustive events such that P(A) = 2P(B) = 3P(C). What is P(B)?

If $$U_{n+1}=3 U_n-2 U_{n-1}$$ and $$U_0=2, U_1=3$$, then $$U_n$$ is equal to

If $$4^n+15n+P$$ is divisible by 9 for all $$n\in N$$, then the least negative integral value of P is

$$(2^{3n}-1)$$ is divisible by

If $$S = {{{2^2} - 1} \over 2} + {{{3^2} - 2} \over 6} + {{{4^2} - 3} \over {12}}\, + \,...$$ upto 10 terms, then S is equal to

$$\sum\limits_{n = 1}^m {n\,.\,n!} $$ is equal to

The first and fifth terms of an A.P. are $$-14$$ and 2 respectively and the sum of its n terms is 40. The value of n is

The solution of the differential equation $${{{d^2}y} \over {d{x^2}}} = 0$$ represents

The solution of the differential equation $$\frac{d y}{d x}+\sqrt{\frac{1-y^2}{1-x^2}}=0$$ is

The solution of the differential equation $$x \frac{d y}{d x}=\cot y$$ is

If ⁿC₃ = 220, then n = ?

A multiple choice examination has 5 questions. Each question has three alternative answers of which exactly one is correct. The probability that a student will get 4 or more correct answer just by guessing, is

If $$\sin A+\sin B=a$$ and $$\cos A+\cos B=b$$, then $$\cos (A+B)$$ equals?

What is $${{\cos \theta } \over {1 - \tan \theta }} + {{\sin \theta } \over {1 - \cot \theta }}$$ equal to?

Find the general solution of $$\sin 2x + \cos x = 0$$.

If $$f(x)+2f(1-x)=x^2+5,\forall$$ real values of $$x$$, then $$f(x)$$ is given by

If $$A=\{3,5,7\}$$ and $$B=\{1,2,3,5\}$$, then $$A \times B \cap B \times A$$ is equal to

Total number of elements in the power set of A containing 17 elements is

The argument of $${{1 - i\sqrt 3 } \over {1 + i\sqrt 3 }}$$ is

Evaluate $${\left[ {{i^{22}} + {{\left( {{1 \over i}} \right)}^{25}}} \right]^3}$$

$${(i + \sqrt 3 )^{100}} + {(i - \sqrt 3 )^{100}} + {2^{100}}$$ is equal to

There are 12 points in a plane out of which 3 points are collinear. How many straight lines can be drawn by joining any two of them?

A regular polygon of n sides has 170 diagonals, then n is equal to

Let the equation of the pair of lines $$y=p x$$ and $$y=q x$$ can be written as $$(y-p x)(y-q x)=0$$. Then the equation of the pair of the angle bisectors of the line $$x^2-4 x y-5 y^2=0$$ is

The distance of the point $$(1,2)$$ from the line $$x+y+2=0$$ measured along the line parallel to $$2 x-y=5$$ is equal to

The slope of lines which makes an angle 45$$^\circ$$ with the line $$2x-y=-7$$

If 2 and 3 are intercepts of a line L = 0, then the distance of L $$\equiv$$ 0 from the origin is

The total number of terms in the expansion of $${(x + y)^{100}} + {(x - y)^{100}}$$ is

The coefficient of $${x^{20}}$$ in the expansion of $${(1 + 3x + 3{x^2} + {x^3})^{20}}$$ is

In the expansion of $${(1 - 3x + 3{x^2} - {x^3})^{2n}}$$, the middle term is

During the phenomenon of resonance

If the earth were to spin faster, acceleration due to gravity at the poles

If heat engine is filled at temperature 27$$^\circ$$C and heat of 100 k cal is taken from source at temperature 677$$^\circ$$C. Work done (in J) is

During $$\alpha$$-decay, atomic mass of parent nuclei is

A point object is placed on the optic axis of a convex lens of focal length $$f$$ at a distance of $$2f$$ to the left of it. The diameter of the lens is $$d$$. An eye is placed at a distance of $$3f$$ to the right of the lens and a distance $$h$$ below the optic axis. The maximum value of $$h$$ to see the image is

For CE transistor amplifier, the audio signal voltage across the collector resistance of 4 k$$\Omega$$ is 5 V. If the current amplification factor of the transistor is 100 and base resistance is 2 k$$\Omega$$, then input signal voltage is

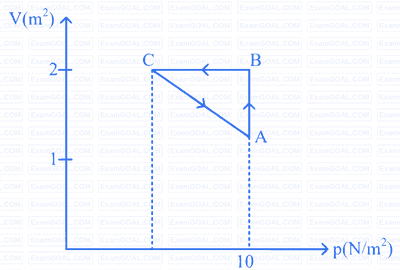
From the following p-V diagram, an ideal gas undergoing a change of state from A to B. Four different processes I, II, III and IV as shown in the figure may lead to same change of state.

A copper and a steel wire of same diameter are connected end to end. A deforming force F$$_1$$ is applied to the wire which causes an elongation of 1 cm. The two wires will have

If kinetic energy of a body is increased by 300%, then percentage change in momentum will be

Which of the following diagram represents the variation of the electric field with distance r from the centre of a uniformly charged non-conducting sphere of radius R?

A DC ammeter and a hot wire ammeter are connected to a circuit in series. When a direct current is passed through circuit, the DC ammeter shows 6 A. When AC current flows through circuit, what is the average readings in DC ammeter and the AC ammeter, if DC and AC currents flows simultaneously through the circuit?

A bullet of mass $m$ hits a mass $$M$$ and gets embedded in it. If the block rises to a height $$h$$ as a result of this collision, the velocity of the bullet before collision is

A particle of mass $$m$$ is moving in a horizontal circle of radius $$r$$ under a centripetal force given by $$\left(\frac{-K}{r^2}\right)$$, where $$K$$ is a constant. Then

The height at which the acceleration due to gravity becomes $$\frac{g}{16}$$ (where, g = acceleration due to gravity on the surface of the earth) in terms of R is, if R is the radius of earth.

Which of the following series spectrum of hydrogen atom lies in ultraviolet region?

Speed of electromagnetic wave in a medium having relative permittivity $$\varepsilon_r$$ and relative permeability $$\mu_r$$ is (speed of light in air, $$c=3\times10^8$$ m/s)

The wavelength of the second line of Balmer series is 486.4 nm. What is the wavelength of the first line of Lyman series?

A bat emitting an ultrasonic wave of frequency 4.5 $$\times$$ 10⁴ Hz at speed of 6 m/s between two parallel walls. The two frequencies heard by the bat will be

A disc of moment of inertia 4 kg - m$$^2$$ revolving with 16 rad/s is placed on another disc of moment of inertia 8 kg - m$$^2$$ revolving 4 rad/s. The angular frequency of composite disc

An electric current $I$ enters and leaves a uniform circular wire of radius $r$ through diametrically opposite points. A charged particle $$q$$ moves along the axis of circular wire passes through its centre with speed $$v$$. The magnetic force on the particle when it passes through the centre has a magnitude

Television frequencies are of the order of 100 MHz, while radio frequencies are of the order of 1 MHz. Using these as typical frequencies, the ratio of the emf generated in a loop antenna by a television wave to that generated by a radio wave, if both have equal electric field intensities.

A particle is performing simple harmonic motion. Equation of its motion is $$x = 5\sin \left( {4t - {\pi \over 6}} \right),x$$ being the displacement from mean position. Velocity (in ms$$^{-1}$$) of the particle at the instant when its displacement is 3, will be

A raft of density 600 g/m$$^3$$ and mass 120 kg floats in water. How much weight can be put on the raft to make it just sink?

The displacement $$x$$ of a particle in a straight line motion is given by $$x=1-t-t^2$$. The correct representation of the motion is

A galvanometer having a resistance of 4 $$\Omega$$ is shunted by a wire of resistance 2 $$\Omega$$. If the total current is 1.5 A, the current passing through shunt is

In Young's double slit experiment, the two slits are separated by 0.2 mm and they are 1 m from the screen. The wavelength of the light used is 500 nm. The distance between 6th maxima and 10th minima on the screen is closest to

A series L-C-R circuit is connected to an AC source of 220 V and 50 Hz shown in figure. If the readings of the three voltmeters $$V_1,V_2$$ and $$V_3$$ are 65 V, 415 V and 204 V respectively, the value of inductance and capacitance will be

A regular hexagon of side $$m$$ which is a wire of length 24 m is coiled on that hexagon. If current in hexagon is $$I$$, then the magnetic moment,

Which of the following gate give the similar output as the output of circuit diagram shown in the figure?

Water is poured in a tank through a cylindrical tube of area of cross-section A and ejecting water at a constant speed 4 m/s. the tank contains a hole of area $$\frac{A}{2}$$ at bottom. Level of water in the tank will not go up beyond

If R and C denote resistance and capacitance of a material, then the dimension of CR will be :

An ideal gas is taken through the cycle A $$\to$$ B $$\to$$ C $$\to$$ A, as shown in the figure. If the net heat supplied to the gas in the cycle is 5 J, the work done by the gas in the process C $$\to$$ A is,

From a circular disc of radius R, a square is cut out with a radius as its diagonal. The centre of mass of remaining portion is at a distance (from the centre)

A bar magnet of length $$6 \mathrm{~cm}$$, is placed in the magnetic meridian with $$N$$ pole, pointing towards the geographical north. Two neutral points, separated by a distance of $$8 \mathrm{~cm}$$ are obtained on the equitorial axis of the magnet. If $$B_H=1.2 \times 10^{-5} \mathrm{~T}$$. Then the pole strength of the magnet is

A force F applied on the wire of radius r and length L and change in the length of the wire is $$l$$. If the same force F is applied on the wire of the same material and radius 4r and length $$4l$$, then change in length of the other wire is,

A 30 mW laser beam has a cross-sectional area of 15 mm². The magnitude of the maximum electric field in this electromagnetic wave is given by

[Permuittivity of space, $$\varepsilon_0=9\times10^{-12}$$

Speed of light, $$c=3\times10^8$$ m/s]

The average kinetic energy of a molecule in air at room temperature of 20$$^\circ$$C

Two guns P and Q can fire bullets at speeds 2 km/s and 4 km/s, respectively. From a point on a horizontal ground, they are fired in all possible directions. The ratio of maximum or areas covered by the bullets fired by the two guns, on the ground is

A cell of emf 2 V is connected with a load of resistance 1.5 $$\Omega$$. The power delivered by the cell to the load is maximum, then power transferred to the load is

A plane glass mirror of thickness 3 cm of material of $$\mu=\frac{3}{2}$$ is silvered on the black surface. When a point object is placed 9 cm from the front surface of the mirror, then the position of the brightest image from the front surface is

Ultraviolet light of wavelength 99 mm falls on a metal plate of work function 1.0 eV. If the mass of the electron is 9.1 $$\times$$ 10$$^{-31}$$ kg, the wavelength of the fastest photoelectron emitted is

In Young's double slit experiment, the fringe width is found to be 0.4 mm. If the whole apparatus is immersed in a liquid of refractive index $$\frac{4}{3}$$ without changing geometrical arrangement, the new fringe width will be

There are two identical containers C$$_1$$ and C$$_2$$ containing to identical gases. Gas in C$$_1$$ is reduced to half of its original volume adiabatically, while the gas in container C$$_2$$ is also reduced to half of its initial volume isothermally. Find the ratio of final pressure in these containers. ($$\gamma$$ be the adiabatic constant).

If K$$_1$$ and K$$_2$$ are maximum kinetic energies of photoelectrons emitted when lights of wavelengths $$\lambda_1$$ and $$\lambda_2$$, respectively incident on a metallic surface and $$\lambda_1=3\lambda_2$$, then

A car is moving with a speed of 54 km/h. If after 3 s, the driver applies brakes and it stops, then how much distance is covered by the car before coming to rest?

A source of sound emits sound waves at frequency $$f_0$$. It is moving towards an observer with fixed speed $${v_s}$$ ($${v_s},v$$, where $$v$$ is the speed of sound in air.) If the observers were to move towards the source with speed $$v_0$$, one of the following two graphs (A and B) will give the correct variation of the frequency $$f$$ heard by the observer as $$v_0$$ is changed.

The variation of $$f$$ with $$v_0$$ is given correctly by

In which mode of transmission, the heat waves travel along straight line with the speed of light?

The escape velocity of a projectile on the earth's surface is 11.2 km/s. A body is projected out with thrice this speed. The speed of the body far away from the earth will be

Consider a compound slab consisting of two different materials having equal lengths, thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is

A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5 A, then the average force on each electron in the coil due to the magnetic field is

With what minimum acceleration can a fireman slide down a rope while breaking strength of the rope is $$\frac{2}{3}$$ of the weight?

The string of length 2 m is fixed at both ends. If the string vibrates in its fourth normal mode with a frequency of 500 Hz, then the waves would travel on it with a velocity of

An alternating voltage = 200 $$\sin 100t$$ is applied to a series combination of $$R=30\Omega$$ and an inductor of 400 mH. The power factor of the circuit is,

In the network shown in figure, the equivalent capacitance between points P and Q is

The resultant of two forces acting at an angle of 120$$^\circ$$ is 10 kg-W and is perpendicular to one of the forces. That force is

Choose the incorrect statements.

Charge on electron is

Two charged spheres of $$-20\mu$$C and $$60\mu$$C are kept at a certain distance. They are touched and kept again at the same distance. What is the ratio of force experienced before and after?

The AC voltage across a resistance can be measured using a