What volume of $0.2 \mathrm{M} \mathrm{CH}_3 \mathrm{COOH}$ needs to be added to 100 ml of $0.4 \mathrm{M} \mathrm{CH}_3 \mathrm{COONa}$ solution to prepare a buffer of pH equal to 4.91 ? ( $\mathrm{pK}_{\mathrm{a}}$ of $\mathrm{CH}_3 \mathrm{COOH}$ is 4.76 )

Identify the final product $[Z]$ formed when Chlorobenzene undergoes the given series of reactions:

Two volatile liquids X and Y form an ideal solution at 298 K and have vapour pressures equal to 100 mm and 200 mm of Hg respectively in their pure state. The mole fraction of X in the solution is 0.4 and the mole fraction of Y in the vapour phase is $a / 20$. Calculate the value of a.

0.4 g of Propane burns completely at 300 K in a bomb calorimeter. The temperature of the calorimeter and surrounding water rises by $0.4^0 \mathrm{C}$. If the heat capacity of the calorimeter and contents is $24 \mathrm{~kJ} \mathrm{~K}^{-1}$ what is the Enthalpy for the reaction? (Assume that propane gas shows ideal behaviour).

Match the metals in Column II with their characteristic properties given in Column I.

	Properties		Metals
A.	Lanthanoid with low value of $3^{\text {rd }}$ ionisation enthalpy.	P	V
B.	f-Block element with electronic configuration $[R n] 6 d^2 7 s^2$	Q	Gd
C.	3 d -series metal whose $\mathrm{M}^{3+}{ }_{(\mathrm{aq})}$ is colourless.	R	Th
D.	3d-series metal with highest $\Delta \mathrm{H}_{\text {(atomisation) }}$	S	Sc

Convert Benzene $\rightarrow 3$-Bromophenol by choosing appropriate reagents [(i) to (v)] in the correct sequence.

(i) $\mathrm{NaNO}_2 / \mathrm{HCl}\left(0^{\circ} \mathrm{C}\right)$

(ii) Conc. $\mathrm{HNO}_3 / \mathrm{H}_2 \mathrm{SO}_4$

(iii) $\mathrm{H}_2 \mathrm{O} / 283 \mathrm{~K}$

(iv) $\mathrm{Fe} / \mathrm{HCl}$

(v) $\mathrm{Br} 2 / \mathrm{Fe}$

Choose the correct statement.

An aqueous solution of $\mathrm{CrCl}_3 .6 \mathrm{H}_2 \mathrm{O}$ (Molar mass $=266.5 \mathrm{~g} / \mathrm{mol}$ ) containing 2.665 g of the solute after processing, when treated with excess of $\mathrm{AgNO}_3$ gave 2.87 g of AgCl (Molar mass of $\mathrm{AgCl}=143.5 \mathrm{~g} / \mathrm{mol}$ ) Choose the correct formula of the compound which give these results.

In which one of the following pairs does the stability of the monovalent ion increase with respect to the molecule, while the magnetic character remains the same for both?

When $9.2 \times 10^{-3} \mathrm{~kg}$ of formic acid is added to 600 ml of water the freezing point of water is depressed. If $30 \%$ of Formic acid undergoes dissociation what would be the freezing point of the solution? ( $\mathrm{K}_{\mathrm{f}}$ of $\mathrm{H}_2 \mathrm{O}$ is 1.86 K kg mol ; MM of formic acid: 46 amu )

An organic compound $[\mathrm{X}]$ (molecular formula- $\mathrm{C}_5 \mathrm{H}_{11} \mathrm{NO}$ when reacted with $\mathrm{Br}_2$ / aq. NaOH yielded $[\mathrm{Y}]$ which reacts with $\mathrm{CHCl}_3$ and Ethanolic KOH to produce a foul smelling compound. Compound $[\mathrm{Y}]$ also reacts with HONO to produce Butan-1-ol with liberation of $\mathrm{N}_2(\mathrm{~g})$. Identify [X].

Choose the correct statement.

Two statements, One Assertion (A) and the other Reason (R) are given. Choose the right option.

Assertion: The rate constant $(\mathrm{k})$ for a chemical reaction gets nearly doubled for a $10^0$ rise in temperature.

Reason: The number of bimolecular collisions between reactant molecules increase with increase in temperature

Which one of the following is a true statement with reference to reaction between 2- Bromo-2-methylpropane and aqueous KOH ?

Which of the following haloalkanes will give more than one isomeric product, on being heated with alc. KOH ?

Which one of the following coordination compounds will exhibit both geometrical and optical isomerism?

The concentration and percentage purity of Oxalic acid can be determined by titration with $\mathrm{KMnO}_4$ in presence of dil. $\mathrm{H}_2 \mathrm{SO}_4$. Instead of dil. $\mathrm{H}_2 \mathrm{SO}_4$, dil HCl cannot be used because

What is the final product $[\mathrm{Z}]$ formed when the given reactions take place?

A non-volatile solute A weighing 60 g when dissolved in 212 g of the solvent Xylene reduces its vapour pressure to $60 \%$. What is the Molar mass of A in $\mathrm{g} / \mathrm{mol}$ ? [MM of xylene $=106 \mathrm{~g} / \mathrm{mol}$ ]

Two statements, one Assertion (A) and the other Reason (R) are given. Choose the correct option.

Assertion: Compound $[\mathrm{X}]$ reacts with Hydrazine in presence of $\mathrm{KOH} /$ Glycol to form the product $[\mathrm{Y}]$.

Reason: Reduction reaction occurs and Carbonyl group is reduced to Methylene group.

For a 1.0 molal solution containing the non-volatile solute Urea, the elevation in boiling point is 2.0 K while the depression in freezing point in a 3.0 molal solution having the same solvent is $4.0 K$. If the ratio $\frac{K_b}{K_f}=\frac{1}{X}$, what is the value of $X$ ?

Identify the correct statement.

Choose the incorrect statement.

Solubility product of the sparingly soluble salt $\mathrm{AgBrO}_3$ in aqueous medium is $9.3 \times 10^{-10}$ Calculate the mass in gram of $\mathrm{AgBrO}_3$ present in 100 ml of its saturated solution. (Molar mass of $\mathrm{AgBrO}_3$ is $236 \mathrm{~g} / \mathrm{mol}$ )

What is the reduction potential of a half-cell consisting of a Pt electrode dipped in $2.2 \mathrm{M} \mathrm{Fe}^{2+}$ and $0.04 \mathrm{M} \mathrm{Fe}^{3+}$ solution where the reaction taking place is conversion of $\mathrm{Fe}^{3+}$ ions to $\mathrm{Fe}^{2+}$ ?

$$\mathrm{E}^0\left(\mathrm{Fe}^{3+} / \mathrm{Fe}^{2+}\right)=0.771 \mathrm{~V}$$

Both reactions (i) and (ii) give the same compound X as the major product. Identify X

(i). 3-Methylbut-1-ene $+\mathrm{HCl} \rightarrow \mathrm{X}$

(ii). Neopentyl alcohol $+\mathrm{HCl}\left(\right.$ anh. $\left.\mathrm{ZnCl}_2\right) \rightarrow \mathrm{X}$

Two chemical reactions of the same order have equal Frequency factor value. Their Activation energies differ by $26.8 \mathrm{~kJ} / \mathrm{mol}$. At 300 K if $k_2=x k_1$ find the value of $x$.

Arrange the following compounds in the decreasing order of the molar conductivities of their aqueous solutions.

A	B	C	D
$\left[\mathrm{Co}\left(\mathrm{NH}_3\right)_5 \mathrm{Cl}\right] \mathrm{Cl}_2$	$\left[\mathrm{Co}\left(\mathrm{NH}_3\right)_3 \mathrm{Cl}_3\right]$	$\left[\mathrm{Co}\left(\mathrm{NH}_3\right)_4 \mathrm{Cl}_2\right] \mathrm{Cl}$	$\left[\mathrm{Co}\left(\mathrm{NH}_3\right)_6\right] \mathrm{Cl}_3$

From the given covalent compounds (A to F) identify the pair of molecules which have:

(i) Two lone pairs of electrons on the central atom.

(ii) One lone pair of electrons on the central atom.

A. $\mathrm{SO}_2$
B. $\mathrm{ClF}_3$
C. $\mathrm{BF}_3$
D. $\mathrm{BrF}_5$
E. XeF ₄
F. $\mathrm{SF}_6$

A current of 2.5 amperes is passed through 800 ml of 0.48 M solution of $\mathrm{CuSO}_4$ for 1.0 hour with a current efficiency of $80 \%$. If the volume of the solution remains unchanged, what is the final molarity of the solution?

A certain orbital having 2 angular nodes and no radial nodes is:

An organic compound $[\mathrm{X}]$ reacts with $\mathrm{H}_2 / \mathrm{Pd}-\mathrm{BaSO}_4$ to give compound $[\mathrm{Y}]$ which reduces Tollen's reagent and undergoes Cannizzaro's reaction. On rigorous oxidation of $[\mathrm{Y}]$ in presence of $\mathrm{KMnO}_4 / \mathrm{H}^{+}$Phthalic acid is the product obtained. What is $[\mathrm{X}]$ ?

Arrange the following free radicals in the increasing order of their stability:

A	B	C	D

If X is a haloalkane with a single Chlorine atom per molecule and the percentage of Cl is 55 , what would be the number of Cl atoms present in 0.1 g of the haloalkane? Atomic mass of $\mathrm{Cl}=35.5 \mathrm{~g} / \mathrm{mol}$

For a reaction $\mathrm{X}_2(\mathrm{l})+\mathrm{Y}_2(\mathrm{~g}) \leftrightharpoons 2 \mathrm{XY}(\mathrm{g})$, the $\Delta \mathrm{H}^0$ and $\Delta \mathrm{S}^0$ are $+29.3 \mathrm{~kJ} / \mathrm{mol}$ and $104.1 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}$ respectively at 298 K . Find the free energy change in $\mathrm{kJ} / \mathrm{mol}$.

Which one of the following reactions does not give the correct combination of reactants and the major products formed in the reaction?

Match the coordination compounds in Column I having the given type of hybridisation of $\mathrm{M}^{\mathrm{n}+}$ ion and magnetic moment as given in Column II.

	Coordination compounds		Hybridisation & Magnetic nature
A.	$\mathrm{Ni}(\mathrm{CO})_4$	P.	$\mathrm{sp}^3, \quad \mu=5.92 \mathrm{BM}$
B.	$\left[\mathrm{Ni}(\mathrm{CN})_4\right]^{2-}$	Q.	$\mathrm{sp}^3, \quad \mu=2.84 \mathrm{BM}$
C.	$\left[\mathrm{Ni}(\mathrm{Cl})_4\right]^{2-}$	R.	$\mathrm{sp}^3, \quad \mu=0$
D.	$\left[\mathrm{MnBr}_4\right]^{2-}$	S.	$\mathrm{dsp}^2, \quad \mu=0$

The EMF of the cell $\mathrm{Al} / \mathrm{Al}^{3+}(0.01 \mathrm{M}) \| \mathrm{Fe}^{2+}(0.02 \mathrm{M}) / \mathrm{Fe}$ is 1.209 V . The EMF of the cell can be increased by

An unsaturated hydrocarbon $[\mathrm{A}]$ undergoes the following series of reactions. Identify $[\mathrm{A}]$.

Identify the compound which gives an optically active haloalkane on reaction with $\mathrm{H}_2$ / Ni on heating.

A	B	C	D

For a given reaction of the type $\frac{3}{5} X(a q) \rightarrow \frac{1}{2} Y(a q)+Z(g)$, the correct expression for the rate of disappearance of $X$ with reference to $Y$ is ___________

Which one of the following statements is correct?.

Given that the standard enthalpy of combustion of $\mathrm{C}_{(\mathrm{S})}$ and $\mathrm{CS}_2(\mathrm{l})$ are -393.3 and $-1108.76 \mathrm{~kJ} / \mathrm{mol}$ respectively and the standard enthalpy of formation of $\mathrm{CS}_2$ is $128.02 \mathrm{~kJ} / \mathrm{mol}$. What is $\Delta H_f^0$ of $\mathrm{SO}_2$ ?

Choose the correct statement.

Benzene diazonium chloride when warmed with water gives a compound, whose Sodium salt when reacted with Allyl bromide gives compound $[\mathrm{X}]$. Identify $[\mathrm{X}]$.

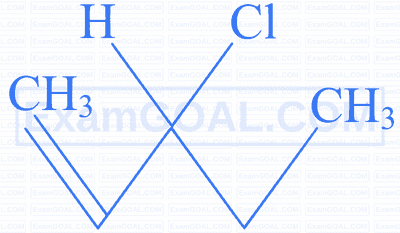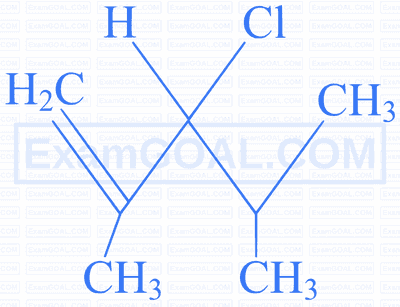Arrange the following in the decreasing order of their $\mathrm{pK}_{\mathrm{a}}$ values.

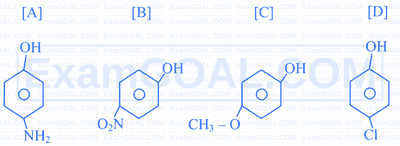
Cyclohexanol undergoes a series of reactions as given. Identify compound (iv).

$\mathrm{C}_6 \mathrm{H}_{11} \mathrm{OH}+\mathrm{CrO}_3 \rightarrow(\mathrm{i})+\mathrm{C}_6 \mathrm{H}_5 \mathrm{MgI} \rightarrow(\mathrm{ii})+$ dil. $\mathrm{HCl} \rightarrow(\mathrm{iii})+$ Conc. $\mathrm{H}_3 \mathrm{PO}_4 \rightarrow(\mathrm{iv})$

Match the structures in Column I with their correct IUPAC names given in Column II.

	Column I		Column II
A.		P.	2,3-Dibromo-1-phenylpentane.
B.		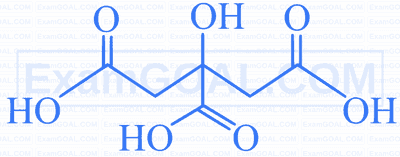Q.	2,3- Dibromohexanedial.
C.		R.	2- ( 4- isobutylphenyl) propanoic acid
D.		S.	2- Hydroxy-1,2,3- propanetricarboxylic acid.

Identify $[\mathrm{X}]$, the final product formed when 2 moles of Ethanal undergoes the following series of reactions with reagents [(i) to (iv)]

Two statements, one Assertion (A) and the other Reason (R) are given. Choose the correct option.

Assertion: Maltose, a disaccharide, is a reducing sugar and is obtained by the partial hydrolysis of starch in presence of the enzyme diastase.

Reason: Hydrolysis of one mole of Maltose gives one mole each of $\alpha-D-$ Glucose and $\beta-D-$ Fructose.

Which one of the following options represents the decreasing order of oxidation number of the central atom in:

$$\mathrm{Cr}_2 \mathrm{O}_7^{2-}, \mathrm{Cr} \mathrm{O}_2^{-}, \mathrm{MnO}_4^{-}, \mathrm{BrO}_3^{-}$$

What is the spin only magnetic moment of the metal ion in $\mathbf{P}$ and the oxidation number of Sulphur in the oxidised product Z ?

The conductivity of 0.01 M solution of $\mathrm{CH}_3 \mathrm{COOH}$ at 298 K is $1.65 \times 10^{-4} \mathrm{Scm}^{-1}$ What is the $\mathrm{pK}_{\mathrm{a}}$ value of the acid if $\lambda^0\left(\mathrm{H}^{+}\right)$and $\lambda^0\left(\mathrm{CH}_3 \mathrm{COO}\right)^{-1}$ are $349.1 \mathrm{Scm}^2 \mathrm{~mol}^{-1}$ and $40.9 \mathrm{Scm}^2 \mathrm{~mol}^{-1}$ respectively?

Two statements, one Assertion (A) and the other Reason (R) are given. Choose the correct option.

Assertion: 2-aminoethanoic acid and p-aminobenzene sulphonic acid can exist as Zwitter ions while p-aminobenzoic acid cannot.

Reason: When the acid group is a relatively strong proton donor and the $-\mathrm{NH}_2$ group is sufficiently basic it can accept a $\mathrm{H}^{+}$ion from the acid group to form the dipolar ion.

$\mathrm{X} \rightarrow 2 \mathrm{Y}$ is a first order reaction where $1.0 \mathrm{~mol} / \mathrm{L}$ of the reactant yields $0.4 \mathrm{~mol} / \mathrm{L}$ of Y in 200 minutes. Calculate the half-life period of the reaction in minutes.

Match the reactions of Glucose given in Column I with the major product formed in the reaction as in Column II.

	Column I - Reactions		Column II - Major product
A.	$\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6+\mathrm{HI}$ (Heat)	P.	$\mathrm{HOOC}-(\mathrm{CHOH})_4-\mathrm{COOH}$
B.	$\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6+\mathrm{Br}_2(\mathrm{aq})$	Q.	$\mathrm{CH}_3-\left(\mathrm{CH}_2\right)_4-\mathrm{CH}_3$
C.	$\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6+$ Conc. $\mathrm{HNO}_3$	R.	$\mathrm{NH}_4 \mathrm{O}-\mathrm{OC}-(\mathrm{CHOH})_4-\mathrm{CH}_2 \mathrm{OH}$
D.	$\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6+2\left[\mathrm{Ag}\left(\mathrm{NH}_3\right)_2\right] \mathrm{OH}$	S.	$\mathrm{HOOC}-(\mathrm{CHOH})_4-\mathrm{CH}_2 \mathrm{OH}$

A certain gas absorbs photon of wavelength $4.0 \times 10^{-7} \mathrm{~m}$ and emits radiation at two wavelengths. If one of the emissions occurs at $7.5 \times 10^{-7} \mathrm{~m}$, what is the wavelength at which the second emission occurs?

The following results were obtained during study of the reaction $2 \mathrm{NO}(\mathrm{g})+\mathrm{Cl}_2(\mathrm{~g}) \rightarrow 2 \mathrm{NOCl}(\mathrm{g})$. Determine the value of $[\mathrm{X}]$ in $\mathrm{mol} / \mathrm{L}$

Experiment	[NO] mol / L	[Cl$_2$] mol / L	Initial rate of formation. [NOCl] mol / L / min
I	0.2	0.2	$6.0 \times 10^{-3}$
II	0.2	0.4	$2.4 \times 10^{-2}$
III	0.4	0.2	$1.2 \times 10^{-2}$
IV	X	0.6	$1.35 \times 10^{-1}$

Two statements, One Assertion [ A ] and the other Reason [ R ] are given. Identify the correct option

Assertion $[A]$ : The decreasing order of the acidic character of the following is $B>D>A>C$

Reason $[\mathbf{R}]$ : Fluorine has larger -I effect than Cl and Br .

The solution of $(x+\log y) d y+y d x=0$ when $y(0)=1$ is

The order of the differential equation $\frac{d}{d x}\left[\left(\frac{d y}{d x}\right)^3\right]=0$ is

Find the value of $\lim\limits_{h \rightarrow 0} \frac{(a+h)^2 \sin (a+h)-a^2 \sin a}{h}$

$0.2+0.22+0.022+\ldots \ldots \ldots$. up to $n$ terms is equal to

The solution set of the system of inequalities $5-4 x \leq-7$ or $5-4 x \geq 7, x \in R$ is

$-\frac{2 \pi}{5}$ is the principal value of

The digits of a three-digit number taken in an order are in geometric progression. If one is added to the middle digit, they form an arithmetic progression. If 594 is subtracted from the number, then a new number with the same digits in reverse order is formed. The original number is divisible by

The least value of ' $a$ ' such that the function $x^2+a x+1$ is increasing on $[1,2]$ is

Three fair dice are thrown. What is the probability of getting a total of 15 given that they exhibit three different numbers that are in arithmetic progression?

The variance of 25 observations is 8 . If each observation is multiplied by 3 , then the new variance of the resulting observations is

P is a point on the line joining the points $(3,5,-1)$ and $(6,3,-2)$. If $y$ coordinate of point P is 2 , then $x$ coordinate will be

If $\vec{a}, \vec{b}, \vec{c}$ are three vectors such that $a \neq 0$ and $\vec{a} \times \vec{b}=2(\vec{a} \times \vec{c}),|\vec{a}|=|\vec{c}|=1,|\vec{b}|=4$ and $|\vec{b} \times \vec{c}|=\sqrt{15}$ if $\vec{b}-2 \vec{c}=\lambda \vec{a}$ then $\lambda^2$ equals :

The general solution of the differential equation $(x-y) d y=(x+y) d x$ is

A line $L_1$ passes through the points $(h, k),(1,2)$ and $(-3,4)$. The points $(4,3)$ and $(h, k)$ lie on the line $L_2$. Given $L_1 \perp L_2$ then $(k-h)$ equals to

Let $M$ be the set of all $2 \times 2$ matrices with entries from the set R of real numbers. Then the function $f: M \rightarrow R$ defined by $f(A)=|A|$ for every $A \in M$ is

The sum of three numbers is 6 . Twice the third number, when added to the first number gives 7 , On adding the sum of the second and third numbers to thrice the first number, we get 12 . The above situation can be represented in matrix form as $A X=B$. Then the $|\operatorname{adj} A|$ is equal to

$\int \frac{1}{\sqrt{9+8 x-x^2}} d x=\varphi(x)+c$ then $\varphi(x)=$

A person writes four letters and address four envelopes. If the letters are placed in the envelopes at random, then the probability that not all letters are placed in the right envelope is

$\int \tan ^2\left(5-\frac{x}{2}\right) d x=$

If $f(x)=\left(\frac{3+x}{1+x}\right)^{2+3 x}$, then $f^{\prime}(0)=$

If $A(t)=\left[\begin{array}{cc}\cos t & \sin t \\ -\sin t & \cos t\end{array}\right]$ then the product of $A(t)$ and $A(-t)$ is

If $A=\left[\begin{array}{cc}1 & -2 \\ 4 & 5\end{array}\right] ; f(t)=t^2-3 t+7$ then $f(A)+\left[\begin{array}{cc}3 & 6 \\ -12 & -9\end{array}\right]=$

Codes used for vehicle identification consists of two distinct English alphabets followed by two distinct digits from 1 to 9 . How many of them end with an even number.

Equation of a circle whose area is 154 sq units and having $2 x-3 y+12=0$ and $x+4 y-5=0$ as diameters is

If $y=\sqrt{\frac{x}{a}}+\sqrt{\frac{a}{x}}, \quad$ then $2 x y \frac{d y}{d x}$ is equal to

Let $A$ and $B$ be two events such that one of the two events must occur. Given that the chance of occurrence of $A$ is $\frac{2}{3}$ the chance of occurrence of $B$, then odds in favour of $B$ is

For two matrices $A$ and $B$, given that $A^{-1}=\frac{1}{8} B$ then inverse of $(8 A)$ is

Distance of the point $(-2,3)$ from the line $12 x-5 y-2=0$ is $\frac{41}{k}$. Then the value of $k$ is

If $\sin A+\sin B=-\frac{21}{65}, \cos A+\cos B=-\frac{27}{65}$ and $\pi

If $A=\left[\begin{array}{ccc}0 & 1 & -2 \\ -1 & 0 & 3 \\ 2 & -3 & 0\end{array}\right]$ then $A^{-1}$

Area of the region bounded by the curve $y=\sin \left(\frac{x}{2}\right)$ between $-4 \pi$ and 0 is

$\int \log x^2 d x=$

The value of $\lambda$ for which the angle between lines $\vec{r}=\hat{\imath}+\hat{\jmath}+\hat{k}+p(2 \hat{\imath}+\hat{\jmath}+2 \hat{k})$ and $\vec{r}=(1+q) \hat{\imath}+(1+q \lambda) \hat{\jmath}+(1+q) \hat{k}$ is $\frac{\pi}{2}$

The value of $\frac{1}{2 \sin 10^{\circ}}-2 \sin 70^{\circ}$ is

If two vertices of a triangle are $(3,-2)$ and $(-2,3)$ and its orthocentre is $(-6,1)$. Then the difference between ordinate and abscissa of the third vertex of the triangle is

The area bounded by the parabola $y^2=36 x$ and its latus rectum is

If $n(A)=3$ and $n(B)=7$ and $A \subseteq B$ then the number of elements in $A \cap B$ is equal to

If $y=\sin ^{-1}\left(\frac{1}{\sqrt{x+1}}\right)$ then $\frac{d y}{d x}=$

$\int_0^\pi \frac{e^{\cos x}}{e^{\cos x}+e^{-\cos x}} d x$ is equal to

The range of $x$ for which the equation $\sin ^{-1}\left(\frac{2 x}{1+x^2}\right)=2 \tan ^{-1} x$ holds true

A spherical snowball is melting such that its volume is decreasing at the rate of $1 \mathrm{~cm}^3 / \mathrm{min}$. The rate at which the diameter is decreasing when the diameter is 10 cm is

For a given Linear Programming problem, the objective function is

$$z=3 x+2 y$$

Subject to constraints are

$$\begin{aligned} & 4 x+3 y \leq 60 \\ & x \geq 3 \\ & y \leq 2 x \\ & y \geq 0 \end{aligned}$$

P is one of the corner points of the feasible region for the given Linear Programming problem. Then the coordinate of P is

The curve $a x^3+b x^2+c x+d$ has a point of minima at $x=1$, then

If $\tan x^{\circ} \tan 2^{\circ} \tan 3^{\circ} \ldots \ldots \ldots \ldots . . \tan 88^{\circ} \tan y^{\circ}=1$ then $\cot (x+y)=$

Vasant and Jothi play a game with a coin. Vasant stakes ₹ 1 and throw the coins four times. If he throws four heads, he gets his stake and ₹3 from Jothi. If he throws only three heads and they are consecutive, he gets his stake and ₹2 from Jothi. If he throws only two heads and they are consecutive, he gets his stake and ₹1 from Jothi. In all other cases Jothi takes the stake money. Find the expectation of Vasant's gain.

The solution of the differential equation $\frac{d y}{d x}+y \log y \cot x=0$ is

A shopkeeper sells three varieties of fruit juice. He has a large number of bottles of same size of each variety. The number of different ways of displaying all the three varieties on the shelf with 5 places in a row and each display must have at least one bottle of each variety is

The value of $\lim _\limits{x \rightarrow 0} \frac{(1-x)^n-1}{x}=$

If $f(x)=\left\{\begin{array}{ll}\frac{1-x^m}{1-x} & \text { if } x \neq 1 \\ 2 m-1 & \text { if } x=1\end{array}\right.$ and the function is discontinuous at $x=1$, then

$\int \frac{d x}{(x+2)\left(x^2+1\right)}=p \log |x+2|+q \log \left|x^2+1\right|+r \tan ^{-1} x+c$ then $p+q+r=$

Let R be a relation on natural numbers defined by $x+2 y=8, x, y \in N$. The domain of R is

Oil from a conical funnel is dripping at the rate of $5 \mathrm{~cm}^3 / \mathrm{s}$. If the radius and height of the funnel are 10 cm and 20 cm respectively, then the rate at which the oil level drops when it is 5 cm from the top is

If the third and fourth terms in the expansion $\left(2 x+\frac{1}{8}\right)^{10}$ are equal, then the value of $x$ is __________

Identify the correct statement

If $\frac{x-1}{3+i}+\frac{y-1}{3-i}=i$ then $(y, x)=$

A line $L_1$ passing through the point A with position vector $\vec{a}=4 \hat{i}+2 \hat{j}+2 \hat{k}$ is parallel to the vector $\vec{b}=2 \hat{i}+3 \hat{j}+6 \hat{k}$. The length of the perpendicular drawn from a point P with position vector $\vec{p}=\hat{i}+2 \hat{j}+3 \hat{k}$ to $L_1$ is

If the distance between the foci is equal to the length of the latus rectum, then the eccentricity of the ellipse is

In an entrance test, there are multiple choice questions. There are four possible answers to each question of which only one is correct. The probability that a student knows the answer to a question is $90 \%$. If he gets the correct answer to a question, then the probability that he was guessing is

The magnitude of the projection of the vector $-\hat{\imath}+2 \hat{\jmath}-\hat{k}$ on the z -axis is

A solid S is made from a cylinder surmounted by a hemisphere on top with both its circular faces sharing a common centre. The radius of cylinder and radius of hemisphere are $x \mathrm{~cm}$. The height of the cylinder is $(20-4 x) \mathrm{cm}$ and the volume of S is $V=\frac{1}{3} \pi y$. Find the maximum value of $y$.

According to Bohr's theory of hydrogen atom, the speed of the electron, its energy and radius of its orbit vary with the principal quantum number $n$, respectively as

A particle of mass $M$ at rest decays into masses $m_1$ and $m_2$ with non-zero velocities. The ratio of de Broglie wavelengths $\lambda_1$ and $\lambda_2$ of the particles is

The nuclear forces

a. are central forces, independent of the spin of the nucleons.

b. have a short-range dominant over a distance of about a few fermi

c. are stronger being hundred times stronger than that of electromagnetic forces.

d. are independent of the nuclear charge.

Which of the above is not true?

Two light rays A and B travel from a medium into air at angles of incidence 15 degrees and 42 degrees respectively. In the medium, light travels 3 cm in 0.2 ns . Will there be total internal reflection? If so, which ray?

An electric field $E=3 x^2 i N C^{-1}$ exists in a certain region of space. The potential difference between the origin and at $x=4 m, V_0-V_4$ is

A current loop consists of two identical semicircular parts each of radius $2 R$, one lying in the $x-y$ plane and the other in $x-z$ plane. If the current in the loop is I, the resultant magnetic field due to two semicircular parts at their common centre is

Which of the following is not a characteristic of diamagnetism?

An ideal inductor is connected across a capacitor. Oscillations of energy $K$ are set up in the circuit. The capacitor plates are slowly drawn apart such that the frequency of oscillations is quadrupled. The work done in the process is

A symmetric double convex lens is cut into two equal parts by a plane perpendicular to the principal axis. If the power of the original lens is 4D, the difference between the powers of the original lens and the cut lens is

Three identical conducting balls $\mathrm{A}, \mathrm{B}$ and C , each of mass m , are thrown upward at an angle $\Theta$ to the horizontal with an initial speed $v$ in a region of space that has a uniform electric field $E$ downward along with the gravitational field $g . A$ is positively charged, B is uncharged and C is negatively charged. Rank the ranges R of these three balls in increasing order.

In a single slit Fraunhofer diffraction pattern obtained at normal incidence, at the angular position of the second diffraction minimum the phase difference (in radian) between the waves from the opposite edges of the slit is

The magnetic flux $\phi$ through a stationary loop of wire having a resistance R varies with time as $\phi=4 t^2+3 t$. The average emf and total charge flowing in the loop in the time interval $t=0$ to $t=\tau$ respectively are

A stone is dropped from a height $h$. It hits the ground with a certain momentum ' $p$ '. If the same stone is dropped from a different height h ' such that percentage change in momentum is $41.4 \%$, then the height from which the stone is dropped is $\mathrm{h}^{\prime}=x \mathrm{~h}$, where $x$ is:

Point charges $-3 Q,-q, 2 q$ and $2 Q$ are placed, one at each corner of a square. The relation between Q and q for which the potential at the centre of the square is zero is

If $R$ and $L$ denote resistance and inductance of a material, then the dimension of $L R$ will be:

A student measures the terminal potential difference $V$ of a cell (emf $\varepsilon$ and internal resistance $r$ ) as a function of current I flowing through it, and draws V versus I graph. The slope and intercept of the graph respectively are

A galvanometer of resistance $50 \Omega$ is connected to a battery of 4 V along with a resistance of $3950 \Omega$ in series. A full-scale deflection of 30 divisions is obtained in the galvanometer. In order to reduce this deflection to 10 divisions, the resistance in series should be equal to:

Two capacitors $\mathrm{C}_1$ and $\mathrm{C}_2$ are charged to 100 V and 120 V respectively. It is found that upon connecting them together in parallel, the potential on each one of them is zero. Therefore

Two very long, straight, parallel wires carry steady currents I and 21 respectively. The distance between the wires is d . At a certain instant of time, a point charge $q$ is at a point equidistant from the two wires, in the plane of the wires. Its instantaneous velocity is v perpendicular to this plane. The magnitude of the force due to the magnetic field acting on the charge at this instant is

A bulb of resistance 280 Ohm is supplied with a voltage $\mathrm{V}=400 \sin \pi \mathrm{t}$. The peak current is

A wooden block floats with $\frac{3}{5}$ of its volume submerged in a tank of water. If a denser liquid is poured into the tank, the wooden block floats with half its volume in the liquid and the remaining half in water. The relative density of the liquid is:

A particle starts from rest and moves along the x -axis with a velocity that varies as $\mathrm{v}=\sqrt{100+4 x} \mathrm{~ms}^{-1}$. The acceleration of the particle is:

One surface of a lens is convex and the other is concave. If the radii of curvatures are $R$ and $r$ respectively, the lens will be convex if

Emission of electrons from a metal plate illuminated with monochromatic electromagnetic radiation will always take place provided

A charged particle is released from rest in a region of space in which steady and uniform electric and magnetic fields are parallel to each other. The particle will move in a

If E is the amplitude of the electric field of the waves starting from the slits in a double slit experiment and $\theta$ is the phase difference between the waves reaching a point on the screen, the ratio of the amplitude of the resultant electric field at that point on the screen to the amplitude at one of the slits is

Two coherent waves of intensities $I_1$ and $I_2$ pass through a region at the same time in the same direction. The sum of maximum to minimum intensities is

A Si and a Ge diode has identical physical dimensions. The band gap in Si is larger than that in Ge. On applying identical reverse bias across these diodes,

A convex lens forms a real image of an object with magnification $m_1$. The lens is moved towards the object to obtain another real image of magnification $m_2$. The image distance is increased by $x$. The focal length of the lens is

For the charge configuration shown here, which of the following is not true?

A bomb of mass 20 kg at rest explodes into two pieces of masses 12 kg and 8 kg . If the velocity of 8 kg mass is $6 \mathrm{~ms}^{-1}$, then the kinetic energy of the other mass is:

Two identical conducting balls having positive charges $q_1$ and $q_2$ are separated by a distance $r$. If they are made to touch each other and then separated to the same distance, the force between them will be

Two simple harmonic motions are represented by equations $y_1=0.5 \sin \left[200 \pi \mathrm{t}+\frac{\pi}{3}\right]$ and $y_1=0.5 \cos \pi \mathrm{t}$. The phase difference of the velocity of particle 1 with respect to the velocity of particle 2 is :

Two identical conductors of lengths 1 and 31 respectively are maintained at the same temperature. They are given potential differences in the ratio $1: 3$. The ratio of their drift velocities is

If voltage across a bulb rated $220 \mathrm{~V}, 50 \mathrm{~W}$ drops by $5 \%$ of its rated value, the percentage of the rated value by which the power would decrease is

A vertical spring of spring constant $24 \mathrm{Nm}^{-1}$ is fixed on a table. A ball of mass 0.5 kg at a height 2 m above the free upper end of the spring falls vertically on the spring so that the spring is compressed by a distance of 50 cm . The net work done in the process is:

The resistance of a wire is 5 ohm at $25^{\circ} \mathrm{C}$ and 7 ohm at $100^{\circ} \mathrm{C}$. The resistance of the wire at $0^{\circ} \mathrm{C}$ is

A sonometer string vibrates with a frequency of 400 Hz . When the length of the string is halved and the tension is altered, it begins to vibrate with a frequency of 200 Hz . The ratio of the new tension to the original tension in the string is:

In an experiment to measure the density of the material of a sphere, an error of $2 \%$ occurred while measuring the radius of a sphere and an error of $3 \%$ occurred while measuring the mass of the sphere. What is the maximum percentage error in the measurement of density?

The radius of earth is $R$ and acceleration due to gravity on its surface is $g$. The height at which the acceleration due to gravity becomes $\frac{g}{8}$ is:

A block of metal A is connected in series with another block of metal B such that the two metal blocks have the same area of cross sections. The thermal conductivity of metal A is K and the free end of metal A is at $80^{\circ} \mathrm{C}$. The temperature of the interface is $60^{\circ} \mathrm{C}$ and the free end of metal B is at $20^{\circ} \mathrm{C}$. Assuming the two metals have the same thickness, the conductivity of metal B is:

The mean energy per molecule for a diatomic gas is:

An LCR series ac circuit is at resonance with 10 V each across $\mathrm{L}, \mathrm{C}$ and R . If the resistance is halved, the respective voltage across $R, C$ and $L$ are

Which, of the following is true of the Balmer series of the hydrogen spectrum?

a. The series is in the visible region.

b. The entire series falls in the ultraviolet region

c. The entire series falls in the infrared region

d. The series is partly in the visible region and partly in the infrared region

If the binding energy per nucleon in $3 \mathrm{Li}^7$ and ${ }_2 \mathrm{He}^4$ nuclei are respectively 5.60 MeV and 7.06 MeV , then energy of $p$ in the reaction $p+{ }_3 \mathrm{Li}^7 \rightarrow 2{ }_2 \mathrm{He}^4$ is

From a circular disc of radius 2 R , a smaller circular disc is cut with radius of the larger disc as its diameter. The centre of the hole is at a distance of $R$ from the centre of the original disc. The distance of the centre of mass of the remaining portion from the centre is:

The ratio of specific heat capacities at constant pressure to that at constant volume for a given mass of a gas is $\frac{5}{2}$. If the percentage increase in volume of the gas while undergoing an adiabatic change is $\frac{3}{2}$, then the percentage decrease in pressure will be:

A planet is 121 times heavier than moon and has a diameter 9 times that of moon. If the escape velocity on the planet is $v$, then the escape velocity on the moon will be:

The electrical conductivity of a semiconductor increases when electromagnetic radiation of wavelength shorter than $1.24 \mu \mathrm{~m}$ is incident on it. The band gap (in eV ) for the semiconductor is

In a nuclear fusion reaction, two nuclei, $A$ and $B$ fuse to produce a nucleus $C$, releasing an amount of energy $\Delta \mathrm{E}$ in the process. If the mass defects of the three nuclei are $\Delta M_A, \Delta M_B$ and $\Delta M_C$ respectively, then which of the following relations is true? ( $c$ is the speed of light).

In the energy band diagram of a material shown below, open circles and filled circles denote holes and electrons respectively. The material is a

A particle moves towards west with a velocity of $10 \mathrm{~ms}^{-1}$. After 10s its direction changes towards south and it moves with the same velocity. The average acceleration of the particle is:

The electric and magnetic fields associated with an electromagnetic wave propagating along +z axis, can be represented by

A bar magnet is oscillating in the earth's magnetic field with a period $T$. When the length of the bar magnet is doubled and its mass is quadrupled, the time period is $T_1$. The ratio of $T_1$ to $T$ is

A cylindrical tank 0.5 m in radius, rests on a platform 1.5 m high. Initially the tank is filled with water to a height of 2.5 m . A small plug whose area is $10^{-4} \mathrm{~m}^2$ is removed from an orifice located on the side of the tank at the bottom. The speed with which the water strikes the ground is: [Assume $g=10 \mathrm{~ms}^{-2}$ ]

A long solenoid has 400 turns. When a current of 100 A is passed through it, the resulting magnetic flux linked with each turn of the solenoid is 4 mWb . The self-inductance of the solenoid is

Which of the following is not true for a perfect conductor?

Young's modulus of the material of wires X and Y are in the ratio 4:1 and the areas of cross sections of the wires X and Y are in the ratio $2: 1$. If the same amount of load is applied to both the wires, the ratio of elongation produced in the wires X and Y will be: (Assume length of the wires X and Y initially are the same)

A force of $-\mathrm{F} \hat{\mathbf{i}}$ acts at the origin of the coordinate system. The torque about the point $(0,1,-1)$ is:

A sample of an ideal gas is taken through the cyclic process ABCA as shown in figure below. It absorbs 60 J of heat during the part AB and rejects 80 J of heat during CA . There is no heat exchanged during the process $\mathrm{BC} . \mathrm{A}$ work of 40 J is done on the gas during the part BC . If the internal energy of the gas at A is 1450 J , then the work done by the gas during the part CA is: