1
GATE CSE 2016 Set 2
Numerical
+2
-0
A complete binary min-heap is made by including each integer in $$[1,1023]$$ exactly once. The depth of a node in the heap is the length of the path from the root of the heap to that node. Thus, the root is at depth $$0.$$ The maximum depth at which integer $$9$$ can appear is ___________.
Your input ____
2
GATE CSE 2016 Set 2
MCQ (Single Correct Answer)
+1
-0.3
The Floyd-Warshall algorithm for all-pair shortest paths computation is based on
3
GATE CSE 2016 Set 2
Numerical
+2
-0
The given diagram shows the flowchart for a recursive function $$A(n).$$ Assume that all statements, except for the recursive calls, have $$O(1)$$ time complexity. If the worst case time complexity of this function is $$O\left( {{n^\alpha }} \right),$$ then the least possible value (accurate up to two decimal positions) of $$\alpha $$ is ____________ .
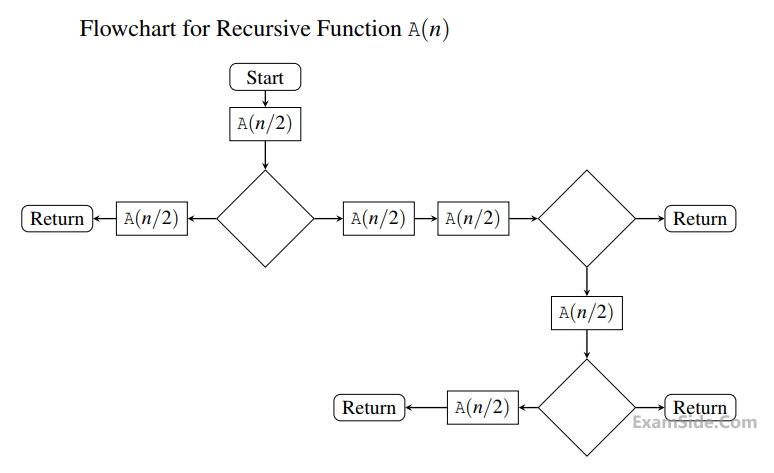

Your input ____
4
GATE CSE 2016 Set 2
Numerical
+2
-0
Let $${A_1},{A_2},{A_3},$$ and $${A_4}$$ be four matrices of dimensions $$10 \times 5,\,\,5 \times 20,\,\,20 \times 10,$$ and $$10 \times 5,\,$$ respectively. The minimum number of scalar multiplications required to find the product $${A_1}{A_2}{A_3}{A_4}$$ using the basic matrix multiplication method is ______________.
Your input ____
Paper analysis
Total Questions
Algorithms
5
Compiler Design
3
Computer Networks
6
Computer Organization
6
Data Structures
5
Database Management System
4
Digital Logic
3
Discrete Mathematics
11
Operating Systems
3
Theory of Computation
6
General Aptitude
10
More papers of GATE CSE
GATE CSE 2025 Set 2
GATE CSE 2025 Set 1
GATE CSE 2024 Set 2
GATE CSE 2024 Set 1
GATE CSE 2023
GATE CSE 2022
GATE CSE 2021 Set 2
GATE CSE 2021 Set 1
GATE CSE 2020
GATE CSE 2019
GATE CSE 2018
GATE CSE 2017 Set 2
GATE CSE 2017 Set 1
GATE CSE 2016 Set 2
GATE CSE 2016 Set 1
GATE CSE 2015 Set 3
GATE CSE 2015 Set 2
GATE CSE 2015 Set 1
GATE CSE 2014 Set 3
GATE CSE 2014 Set 2
GATE CSE 2014 Set 1
GATE CSE 2013
GATE CSE 2012
GATE CSE 2011
GATE CSE 2010
GATE CSE 2009
GATE CSE 2008
GATE CSE 2007
GATE CSE 2006
GATE CSE 2005
GATE CSE 2004
GATE CSE 2003
GATE CSE 2002
GATE CSE 2001
GATE CSE 2000
GATE CSE 1999
GATE CSE 1998
GATE CSE 1997
GATE CSE 1996
GATE CSE 1995
GATE CSE 1994
GATE CSE 1993
GATE CSE 1992
GATE CSE 1991
GATE CSE 1990
GATE CSE 1989
GATE CSE 1988
GATE CSE 1987
GATE CSE
Papers
2023
2022
2020
2019
2018
2013
2012
2011
2010
2009
2008
2007
2006
2005
2004
2003
2002
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
1991
1990
1989
1988
1987