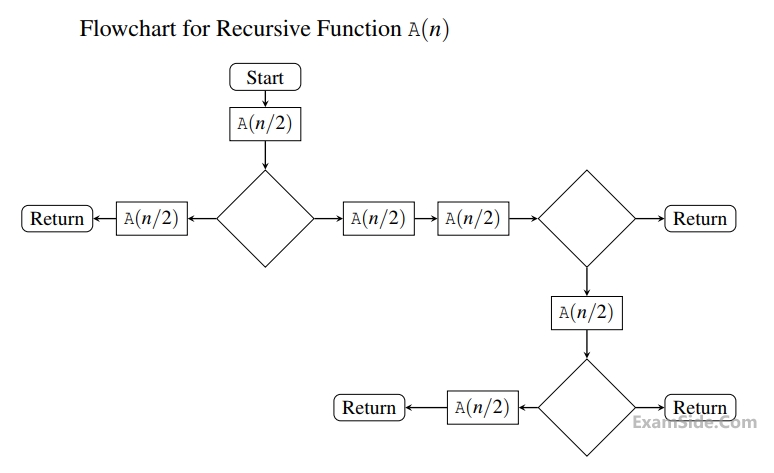
The given diagram shows the flowchart for a recursive function $$A(n).$$ Assume that all statements, except for the recursive calls, have $$O(1)$$ time complexity. If the worst case time complexity of this function is $$O\left( {{n^\alpha }} \right),$$ then the least possible value (accurate up to two decimal positions) of $$\alpha $$ is ____________ .

Let $${A_1},{A_2},{A_3},$$ and $${A_4}$$ be four matrices of dimensions $$10 \times 5,\,\,5 \times 20,\,\,20 \times 10,$$ and $$10 \times 5,\,$$ respectively. The minimum number of scalar multiplications required to find the product $${A_1}{A_2}{A_3}{A_4}$$ using the basic matrix multiplication method is ______________.

Assume that the algorithms considered here sort the input sequences in ascending order. If the input is already in ascending order, which of the following are TRUE?

$$\,\,\,\,\,\,\,{\rm I}.\,\,\,\,\,\,\,$$ Quicksort runs in $$\Theta \left( {{n^2}} \right)$$ time
$$\,\,\,\,\,{\rm I}{\rm I}.\,\,\,\,\,\,\,$$ Bubblesort runs in $$\Theta \left( {{n^2}} \right)$$ time
$$\,\,\,{\rm I}{\rm I}{\rm I}.\,\,\,\,\,\,\,$$ Mergesort runs in $$\Theta \left( n \right)$$ time
$$\,\,\,{\rm I}V.\,\,\,\,\,\,\,$$ Insertion sort runs in $$\Theta \left( n \right)$$ time

Match the following:

GROUP - 1	GROUP - 2
(P) Lexical analysis	(i) Leftmost derivation
(Q) Top down parsing	(ii) Type checking
(R) Semantic analysis	(iii) Regular expressions
(S) Runtime environments	(iv) Activation records