1
GATE CSE 2015 Set 1
Numerical
+2
-0
The graph shown below has 8 edges with distinct integer edge weights. The minimum spanning tree (MST) is of weight 36 and contains the edges: {(A, C), (B, C), (B, E), (E, F), (D, F)}. The edge weights of only those edges which are in the MST are given in the figure shown below. The minimum possible sum of weights of all 8 edges of this graph is ___________.
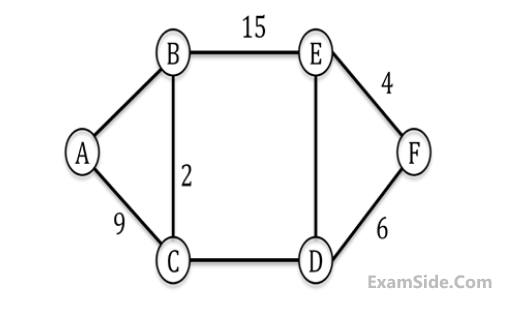

Your input ____
2
GATE CSE 2015 Set 1
MCQ (Single Correct Answer)
+1
-0.3
Which one of the following is the recurrence equation for the worst case time complexity of the Quicksort algorithm for sorting n ( $$ \ge 2$$ ) numbers? In the recurrence equations given in the options below, c is a constant.
3
GATE CSE 2015 Set 1
MCQ (Single Correct Answer)
+1
-0.3
Match the following:
(Q) Floyd-Warshall algorithm for all pairs shortest paths
(R) Mergesort
(S) Hamiltonian circuit
(ii) Greedy method
(iii) Dynamic programming
(iv) Divide and conquer
List 1
(P) Prim’s algorithm for minimum spanning tree(Q) Floyd-Warshall algorithm for all pairs shortest paths
(R) Mergesort
(S) Hamiltonian circuit
List 2
(i) Backtracking(ii) Greedy method
(iii) Dynamic programming
(iv) Divide and conquer
4
GATE CSE 2015 Set 1
MCQ (Single Correct Answer)
+2
-0.6
Consider a max heap, represented by the array: 40, 30, 20, 10, 15, 16, 17, 8, 4.
| Array Index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Value | 40 | 30 | 20 | 10 | 15 | 16 | 17 | 8 | 4 |
Now consider that a value 35 is inserted into this heap. After insertion, the new heap is
Paper analysis
Total Questions
Algorithms
6
Compiler Design
3
Computer Networks
6
Computer Organization
3
Data Structures
4
Database Management System
4
Digital Logic
4
Discrete Mathematics
12
Operating Systems
6
Programming Languages
3
Software Engineering
2
Theory of Computation
3
Web Technologies
1
General Aptitude
10
More papers of GATE CSE
GATE CSE 2025 Set 2
GATE CSE 2025 Set 1
GATE CSE 2024 Set 2
GATE CSE 2024 Set 1
GATE CSE 2023
GATE CSE 2022
GATE CSE 2021 Set 2
GATE CSE 2021 Set 1
GATE CSE 2020
GATE CSE 2019
GATE CSE 2018
GATE CSE 2017 Set 1
GATE CSE 2017 Set 2
GATE CSE 2016 Set 1
GATE CSE 2016 Set 2
GATE CSE 2015 Set 3
GATE CSE 2015 Set 1
GATE CSE 2015 Set 2
GATE CSE 2014 Set 3
GATE CSE 2014 Set 1
GATE CSE 2014 Set 2
GATE CSE 2013
GATE CSE 2012
GATE CSE 2011
GATE CSE 2010
GATE CSE 2009
GATE CSE 2008
GATE CSE 2007
GATE CSE 2006
GATE CSE 2005
GATE CSE 2004
GATE CSE 2003
GATE CSE 2002
GATE CSE 2001
GATE CSE 2000
GATE CSE 1999
GATE CSE 1998
GATE CSE 1997
GATE CSE 1996
GATE CSE 1995
GATE CSE 1994
GATE CSE 1993
GATE CSE 1992
GATE CSE 1991
GATE CSE 1990
GATE CSE 1989
GATE CSE 1988
GATE CSE 1987
GATE CSE
Papers
2023
2022
2020
2019
2018
2013
2012
2011
2010
2009
2008
2007
2006
2005
2004
2003
2002
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
1991
1990
1989
1988
1987