Let G be a connected planar graph with 10 vertices. If the number of edges on each face is three, then the number of edges in G is ___________.

$$\sum\limits_{x = 1}^{99} {{1 \over {x\left( {x + 1} \right)}}} $$ = _____________.

Suppose L = { p, q, r, s, t } is a lattice represented by the following Hasse diagram: 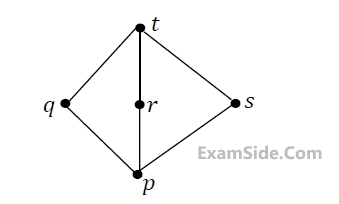For any $$x, y ∈ L$$, not necessarily distinct, $$x ∨ y$$ and x ∧ y are join and meet of x, y, respectively. Let $$L^3 = \left\{\left(x, y, z\right): x, y, z ∈ L\right\}$$ be the set of all ordered triplets of the elements of L. Let p_r be the probability that an element $$\left(x, y,z\right) ∈ L^3$$ chosen equiprobably satisfies $$x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z)$$. Then

The probabilities that a student passes in Mathematics, Physics and Chemistry are $$m, p$$ and $$c$$ respectively. Of these subjects, the student has $$75$$% chance of passing in at least one, a $$50$$% chance of passing in at least two and a $$40$$% chance of passing in exactly two. Following relations are drawn in $$m, p, c:$$
$${\rm I}.$$ $$\,\,\,\,\,\,$$ $$p+m+c=27/20$$
$${\rm I}{\rm I}.$$ $$\,\,\,\,\,\,$$ $$p+m+c=13/20$$
$${\rm I}{\rm I}{\rm I}.$$ $$\,\,\,\,\,\,$$ $$\left( p \right) \times \left( m \right) \times \left( c \right) = 1/10$$