COMEDK 2025 Afternoon Shift

Paper was held on Sat, May 10, 2025 7:30 AM

Chemistry

An organic compound $\mathrm{A}\left(\mathrm{C}_5 \mathrm{H}_9 \mathrm{~N}\right)$ upon reaction with $\mathrm{Na} / \mathrm{Hg} / \mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}$ gives compound B . B reacts with $\mathrm{NaNO}_2 / \mathrm{HCl}$ at 274 K to form C with quantitative liberation of $\mathrm{N}_2$ gas. B also reacts with Hinsberg's reagent to form a compound which is soluble in alkali. Identify compound B.

The $E_{M^{3+} / M^{2+}}^o$ values for $\mathrm{Cr}, \mathrm{Mn}, \mathrm{Fe}$ and Co are $-0.41,+1.57,+0.77$ and +1.97 V respectively.

For which of these metals, the change in oxidation state from +2 to +3 is the easiest?

Given are 4 pairs of covalent molecules. Identify the pair in which both molecules have the same shape.

Lead storage battery contains $4.25 \mathrm{M} \mathrm{H}_2 \mathrm{SO}_4$ which has a density of $1.24 \mathrm{~g} / \mathrm{ml}$. Calculate the molality of aqueous solution of $\mathrm{H}_2 \mathrm{SO}_4$.

Which of the following is the correct name according to IUPAC rules?

The Enthalpy of combustion of 1.0 mole of a reactive metal X at $27^{\circ} \mathrm{C}$ and 1.0 bar pressure to form a solid oxide ( XO ) is $-601.83 \mathrm{~kJ} / \mathrm{mol}$. The Internal energy change for this reaction is ___________ kJ. $$\left(\mathrm{R}=8.314 \mathrm{j} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right)$$

The ionisation constant of the weak acid HF whose concentration is 0.1 M is $3.5 \times 10^{-4}$ The Equilibrium constant value for the reaction $\mathrm{F}^{-}+\mathrm{H}_2 \mathrm{O} \leftrightharpoons \mathrm{HF}+\mathrm{OH}^{-}$is _________ and the pH of aqueous solution of the weak acid is __________ .

An Alkene " X " on reaction with hot acidified $\mathrm{KMnO}_4$ gave a mixture of Ethanoic acid and Propanone. Identify " X ".

Imagine an R - moiety of a pentapeptide molecule having one $-\mathrm{SH},-\mathrm{CONH}_2,-\mathrm{NH}_2$ groups each and two $-$COOH groups in the amino acids forming the pentapeptide. If the pH is maintained at 13.2, what would be the total number of negative charges on the pentapeptide?

An aqueous solution which contains $42 \%$ by weight $(\mathrm{w} / \mathrm{W})$ of a volatile liquid "A" of molar mass of $140 \mathrm{~g} / \mathrm{mol}$, has a vapour pressure of 2141.4 mm of Hg at $37^{\circ} \mathrm{C}$. What is the vapour pressure of the pure liquid " A "? Vapour pressure of water at $37^{\circ} \mathrm{C}$ is 2019.1 mm .

What would be the cell potential for the Galvanic cell which is represented by the electrochemical reaction: $$ \begin{aligned} & 2 \mathrm{Cr}_{(\mathrm{S})}+3 \mathrm{Fe}^{2+}(0.02 \mathrm{M}) \rightarrow 2 \mathrm{Cr}^{3+}(0.2 \mathrm{M})+3 \mathrm{Fe} \\ & \mathrm{E}^0 \mathrm{Fe}^{2+} / \mathrm{Fe}=-0.42 \mathrm{~V} \quad \mathrm{E}^0 \mathrm{Cr}^{3+} / \mathrm{Cr}=-0.72 \mathrm{~V} \end{aligned} $$

The hydrogenation of Ethyne is carried out at 600 K . The same reaction when carried out in presence of a catalyst maintaining the same rate constant, the temperature required is only 400 K . If the catalyst lowers the Activation energy of the reaction by $20 \mathrm{~kJ} / \mathrm{mol}$, what is the value of $\mathrm{E}_{\mathrm{a}}$ ?

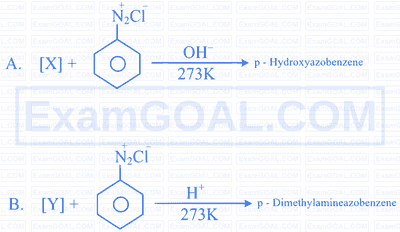
Complete the following 2 reactions A \& B by choosing appropriate reactants $[\mathrm{X}] \&[\mathrm{Y}]$.

The time needed for completion of $80 \%$ is $y$ times the half-life period of a first order reaction. What is the value of $y$ ?

A current of 1.5 A is passed for 2 hours through an aqueous solution of $\mathrm{PdX} \mathrm{n}_{\mathrm{n}}$ where X is a monovalent anion. During the electrolysis process 2.977 g of Palladium metal gets deposited at the cathode. Calculate the charge on Pd ions. (Atomic mass of $\mathrm{Pd}=106.4 \mathrm{~g} / \mathrm{mol}$ ).

Choose the statements which are incorrect in the case of Lanthanoids.

A. $\mathrm{Ce}^{4+}$ is diamagnetic while $\mathrm{Sm}^{3+}$ is paramagnetic.

B. The atomic size of the transition metals having atomic number greater than 71 are very close to that of the elements above them.

C. Lanthanoids react with hot water forming water soluble $\mathrm{Ln}(\mathrm{OH})_3$ with the liberation of $\mathrm{O}_2$.

D. The general electronic configuration of Lanthanoids is $(n-2) \mathrm{f}^{1-14} 5 \mathrm{~d}^0 6 \mathrm{~s}^2$, where $n=6$.

Larger number of oxidation states are exhibited by the actinoids than those of lanthanoids. The reason is:

Given below are 2 statements: one Assertion and the other Reason. Which one of the following options is correct?

Assertion : Sulphur dioxide and Hydrogen peroxide can act as both oxidising and reducing agents but Nitric acid can act as only oxidising agent.

Reason : Sulphur and Oxygen can exhibit more than one stable oxidation states while Nitrogen does not.

From among the 4 given compounds identify the compounds which possess a net dipole moment.

A. cis-1,2-Dichloroethene

B. Tetrachloromethane

C. o-Dichlorobenzene

D. trans 2,3-Dibromobut-2-ene

Which is the correct order of increasing number of unpaired electrons in the following ions?

$$\mathrm{A}=\mathrm{Cr}^{2+}(\mathrm{Z}=24) \mathrm{B}=\mathrm{Cu}^{2+}(\mathrm{Z}=29) \quad \mathrm{C}=\mathrm{Ni}^{2+}(\mathrm{Z}=28) \mathrm{D}=\mathrm{Fe}^{3+}(\mathrm{Z}=26)$$

Which one of the following is incorrect?

A dilute solution of $\mathrm{K}_2 \mathrm{HgI}_4$ reagent is $95 \%$ ionised. What would be the approximate value of its van't Hoff factor?

For a hypothetical chemical reaction $\mathrm{A}_2+3 \mathrm{~B}_2+$ Heat $\cdots\rightarrow 2 \mathrm{AB}_3$, which one of the following combinations of state variables would support the spontaneity of the reaction at a particular temperature?

Choose the incorrect statement from the following.

Which one of the following compounds will give a yellow precipitate when reacted with $\mathrm{I}_2 / \mathrm{NaOH}$?

Identify X and Y formed in the following two reactions.

(i) Decan-1-ol $\xrightarrow{\text { Jones reagent }} \mathrm{X}$

(ii). Sodium salt of $\mathrm{X} \xrightarrow{\mathrm{NaOH} / \mathrm{CaO}, \Delta} \mathrm{Y}$

Choose the incorrect statement.

Match A, B, C and D with the appropriate functions given.

	Column I		Functions
A.	Oxidoreductase	P.	Malfunctioning leads to Addison's disease.
B.	Phosphodiester bonds	Q.	Regulates responses to external stimuli.
C.	Adrenal cortex	R.	Catalyses glycolysis.
D.	Epinephrine	S.	Links nucleotides together.

Two statements, One Assertion and the other Reason, are given.

Which one of the following is the correct option?

Assertion: The acid strength of 4 compounds in the descending order is p- Nitrophenol > p-Methoxyphenol > Phenol > p-chlorophenol.

Reason: Electron withdrawing groups increase the acid strength while Electron donating groups decrease the acid strength of Phenol and its derivatives.

Identify the incorrect statement.

Arrange the following ions in the decreasing order of covalent double bonds formed by the transition metal with oxygen.

A. $=$ chromate $\mathrm{B}=$ permanganate $\mathrm{C}=$ dichromate

Which one of the following structures in Column I does not have the correct IUPAC name as given in Column II.

S.No.	Structure		IUPAC name
A.	$\left[\mathrm{CoBr}_2(\mathrm{en})_2\right] \mathrm{Cl}$	P.	Dibromidodi-( ethan-1, 2 - diamine)cobalt (III) chloride
B.	$\mathrm{Na}\left[\mathrm{PtBrCl}\left(\mathrm{NO}_2\right)\left(\mathrm{NH}_3\right)\right]$	Q.	Sodium amminebromidochloridonitrito- N - palatinate(II)
C.	$\left[\mathrm{Cr}\left(\mathrm{H}_2 \mathrm{O}\right)_2\left(\mathrm{NH}_3\right)_4 \mathrm{Cl}\right] \mathrm{SO}_4$	R.	Tetraamminediaquachloridochromium (III) sulphate.
D.	$\left[\mathrm{Pt}\left(\mathrm{NH}_3\right)_4\right]\left[\mathrm{PtCl}_4\right]$	S.	Tetraammineplatinum (II) tetrachloridoplatinate (II)

When $0.4 \mathrm{~g} \mathrm{CH}_3 \mathrm{COOH}$ is added to 40 g of Benzene to form a solution, the freezing point is depressed by $0.45^{\circ} \mathrm{C}$. If Acetic acid undergoes dimerisation in Benzene ( $\mathrm{K}_{\mathrm{f}}=5.12 \mathrm{~K} \mathrm{~kg} / \mathrm{mol}$ ) what is the percentage association of the acid in Benzene?

Two subatomic particles 1 and 2, with the same kinetic energies have their de- Broglie wavelengths as $\lambda_1 \& \lambda_2$ and masses as 3 m and 6 m respectively. Determine the ratio $\lambda_1: \lambda_2$.

Identify the product $(\mathrm{Y})$ formed in the given reaction and the name of the reaction where $(\mathrm{X}) \rightarrow(\mathrm{Y})$.

Choose the correct statement:

A transition metal M forms 4 homoleptic octahedral coordination compounds, $\mathrm{A}, \mathrm{B}, \mathrm{C}$ and D of the type $\left[\mathrm{MX}_6\right]^{z-}$ with monodentate ligands a, b, c and d respectively. These compounds absorb red. blue. yellow and blue-green light respectively. Which one of the options shows the correct order of decreasing ligand strength?

Which one of the following is the correct statement?

(i) and (ii) are 2 chemical reactions carried out at TK.

(i). $\mathrm{X} \rightarrow \mathrm{Y}+\mathrm{W}$ with $\mathrm{k}_1$ as rate constant.

(ii). $\mathrm{X} \rightarrow \mathrm{Z}+\mathrm{W}$ with $k_2$ as rate constant.

The Activation energy for reaction (ii) is 3 times that of reaction (i). What is the expression for $k_1$ ?

Which one of the following is the major product formed when the given reaction occurs?

Toluene when reacted with $\mathrm{Cl}_2$ gas at 385 K forms a product X which undergoes further reaction with Sodium ethoxide to yield product Y . The structure of Y is ___________ .

A dilute solution of an ionic compound $\mathrm{A}_3 \mathrm{~B}$ has an Osmotic pressure which is 6 times that of $0.02 \mathrm{M} \mathrm{MgCl}_2$. What is the molar concentration of $\mathrm{A}_3 \mathrm{~B}$ assuming that it undergoes complete dissociation in water?

An organic compound " A " reacts with $\mathrm{Zn} / \mathrm{Hg}$ / Conc. HCl to form p-Xylene. It reduces Tollen's reagent and on oxidation with $\mathrm{KMnO}_4 / \mathrm{H}^{+}$it yields 1, 4-benzenedicarboxylic acid. Identify compound A.

The first ionisation enthalpy of Al in $\mathrm{kJ} \mathrm{mol}^{-1}$ is: [Given the first ionisation enthalpy of $\mathrm{Na}, \mathrm{Mg}$ and Si in $\mathrm{kJ} \mathrm{mol}^{-1}$ are 497,738 and 787 respectively]

Choose the coordination compound which does not exhibit Optical activity.

Identify the reagents to be used to complete the given reaction.

What is the standard electrode potential at 298 K for the reaction: $\mathrm{Cu}^{2+}+1 \mathrm{e}-\rightarrow \mathrm{Cu}^{+1}$ ?

Given: $\mathrm{E}_0 \mathrm{Cu}^{+1} / \mathrm{Cu}=0.5 \mathrm{~V} \quad \& \quad \mathrm{E}_0 \mathrm{Cu}^{+2} / \mathrm{Cu}=0.335 \mathrm{~V}$

Which one of the following molecules attains greater stability on formation of its diatomic monovalent anion?

The Standard Reduction potential at $25^{\circ} \mathrm{C}$ for $\left(\mathrm{MnO}_4\right)^{-1} / \mathrm{H}^{+}$is +1.49 V . The $\mathrm{E}^0$ values for four Metal ions :

(a). $\mathrm{Co}^{3+} / \mathrm{Co}^{2+}$

(b). $\mathrm{Cr}^{3+} / \mathrm{Cr}$

(c). $\mathrm{Au}^{3+} / \mathrm{Au}$ and

(d). $\mathrm{Ag}^{+} / \mathrm{Ag}$

are $+1.81 \mathrm{~V},-0.74 \mathrm{~V},+1.50 \mathrm{~V}$ and +0.8 V respectively. Identify two of them which cannot be oxidised by $\left(\mathrm{MnO}_4\right)^{-1} / \mathrm{H}^{+}$

The best method for the separation of $o$-nitrophenol and $p$-nitrophenol from their mixture is :

For the reaction $\mathrm{A}_2+\mathrm{B}_2 \cdots \cdots>2 \mathrm{AB}, \Delta \mathrm{H}_{\mathrm{f}}=-400 \mathrm{~kJ} / \mathrm{mol}$. The bond dissociation enthalpies of $\mathrm{A}_2$, $\mathrm{B}_2$ and AB are in the ratio $1: 0.75: 1$. What is the bond dissociation enthalpy of $\mathrm{B}_2$ in $\mathrm{kJ} / \mathrm{mol}$ ?

The correct order of spin only magnetic moments among the following is: [Given: Atomic numbers: $\mathrm{Mn}=25, \mathrm{Fe}=26, \mathrm{Co}=27$ ]

Choose the incorrect statement from the following.

Match the reactions in Column I with the correct products given in Column II

S.No.	Column I	S.NO.	Column II
A.	1- Chloropropane $+(\mathrm{Zn} / \mathrm{HCl}) \rightarrow$	P.	Propanone + Methanal
B.	n- Hexane $+\left(\right.$ anh. $\left.\mathrm{AlCl}_3 / \mathrm{HCl}_{(\mathrm{g})}\right) \rightarrow$	Q.	Propanone
C.	2- Methylpropene $+\left(\mathrm{O}_3 \& \mathrm{Zn} / \mathrm{H}_2 \mathrm{O}\right) \rightarrow$	R.	Propane
D.	Propyne $+\left(\mathrm{HgSO}_4 / \mathrm{H}_2 \mathrm{SO}_4\right.$ at 333 K$) \rightarrow$	S.	2-Methylpentane + 3-Methylpentane

The rate constant for a zero order reaction $\mathrm{A} \rightarrow \mathrm{B}+\mathrm{C}$ is $6.0 \times 10^{-3} \mathrm{molL}^{-1} \mathrm{~s}^{-1}$. What would be the time taken for the initial concentration of A to decrease from 0.2 M to 0.024 M ?

When one mole of a hydrocarbon $\mathbf{C}_{\mathbf{a}} \mathbf{H}_{\mathbf{b}}$ undergoes complete combustion, it requires 7.5 moles of $\mathrm{O}_2$ and results in the production of 6 moles of $\mathrm{CO}_2$. Calculate the values of $\mathbf{a}$ and $\mathbf{b}$.

For the reaction $\mathrm{P}+\mathrm{Q} \leq \mathrm{R}+\mathrm{S}$, carried out at 298 K , the equilibrium constant was found to be 169 and the initial concentrations of all reactants and products was 1.0 M . What is the equilibrium concentration of the reactants?

Two statements, one Assertion and the other Reason are given. Choose the correct option.

Assertion: Heterocyclic compounds like Pyridine and Thiophene are non-aromatic compounds.

Reason: According to Huckel rule for a given compound to exhibit aromaticity, the molecule must be planar, cyclic system having delocalised $(4 n+2) \pi$ electrons.

Match the reaction in Column I with the major product formed given in Column II.

		Column II - Product
A.	P.	Pentan-2-ol
B.	Q.	2-Hydroxybenzoic acid.
C.	R.	Phenol
D.	S.	2-Methylpropan-1-ol

Two statements, one Assertion and the other Reason are given. Choose the correct option.

Assertion: For strong electrolytes the plot of Molar conductivity versus Concentration gives a straight line with slope equal to +A and intercept equal to $\lambda_{\mathrm{m}}$

Reason: For strong electrolytes, $\lambda_{\mathrm{m}}$ increases slowly with dilution due to increase in the distance between the ions and increase in ionic mobility

Mathematics

The terms of an infinitely decreasing geometric progression in which all the terms are positive, the first term is $\mathbf{4}$, and the difference between third and fifth term is $\frac{32}{81}$, then which of the following is not true

For real numbers $x$ and $y, x R y \Leftrightarrow x-y+\sqrt{2}$ is an irrational number. Then the relation R is:

Let $A=\{x: x=4 n+1, n \in Z, 0 \leq n<4\}$

$$\begin{aligned} & B=\{x: x=15 n+4, n \in N, n \leq 3\} \\ & C=\{x: x \text { is a prime number }, x \in A \cup B\} \end{aligned}$$

Then the cardinal number of set C is

If $ 2 y=\left[\cot ^{-1}\left(\frac{\sqrt{3} \cos x+\sin x}{\cos x-\sqrt{3} \sin x}\right)\right]^2 \forall x \in\left(0, \frac{\pi}{2}\right)$ then $\frac{d y}{d x}$ is equal to :

Five persons entered the lift cabin on the ground floor of an eight-floor apartment. Suppose that each of them independently and with equal probability, can leave the cabin at any floor beginning with the first floor, then the probability of all five persons leaving at different floors is :

If $\cos A=\frac{3}{4}$, then $\left(32 \sin \frac{A}{2} \sin \frac{5 A}{2}\right)=$

If $A=\frac{1}{\pi}\left[\begin{array}{cc}\sin ^{-1} \frac{1}{2} & \tan ^{-1} \frac{x}{\pi} \\ \sin ^{-1} \frac{x}{\pi} & \cot ^{-1} \sqrt{3}\end{array}\right] \quad B=\frac{1}{\pi}\left[\begin{array}{cc}-\cos ^{-1} \frac{1}{2} & \tan ^{-1} \frac{x}{\pi} \\ \sin ^{-1} \frac{x}{\pi} & -\tan ^{-1} \sqrt{3}\end{array}\right]$ and I is an identity matrix of order $2 \times 2$, then $A-B=$

The length of the latus rectum of a conic $49 y^2-16 x^2=784$ is

The curve $4 y=3 x^4-2 x^2$ attains ----------- at the points $x=-\frac{1}{\sqrt{3}}$ and $x=\frac{1}{\sqrt{3}}$

The area of the region enclosed by the lines $2 x+y=10, y=1, y=5$ and the $y$-axis is

$x=a(\theta+\sin \theta)$ and $y=a(1-\cos \theta)$ represents the equation of a curve. If $\theta$ changes at a constant rate $k$ then the rate of change of the slope of the tangent to the curve at $\theta=\frac{\pi}{3}$ is

The function $f(x)=\left\{\begin{array}{l}\frac{|x|}{x}, \text { if } x \neq 0 \\ 0, \text { if } x=0\end{array}\right.$ is discontinuous at

Integrating factor of the differential equation $\frac{d y}{d x}+y=\frac{x^3+y}{x}$ is

If $y=\left(\sin ^{-1} x\right)^2+\left(\cos ^{-1} x\right)^2$,

then $\left(1-x^2\right) \frac{d^2 y}{d x^2}-x \frac{d y}{d x}=$

If ${ }^{n+2} C_8:{ }^{n-2} P_4=57: 16$, then ' $n$ ' is

Differentiate $\log _a x$ with respect to $a^x$

On each working day of a school there are six periods. The number of ways in which five subjects are arranged if each subject is allotted at least one period and no period remains vacant is

A bag contains $(n+1)$ coins. It is known that one of these coins has a head on both sides, whereas the other coins are fair. One of these coins is selected at random and tossed. If the probability that the toss results in heads is $\frac{7}{12}$, then the value of $n$ is :

Quadrilateral PQRS is inscribed inside a rectangle of dimensions $10 \mathrm{~cm} \times 8 \mathrm{~cm}$. The value of ' $x$ ', if the area of the quadrilateral is minimum is

If $A=\left[\begin{array}{ccc}0 & -1 & 2 \\ 1 & 0 & 3 \\ -2 & -3 & 0\end{array}\right]$, then $A+2 A^T=$

Simplified expression of

$1-\frac{\sin ^2 y}{1+\cos y}+\frac{1+\cos y}{\sin y}-\frac{\sin y}{1-\cos y}$ is :

The length of the perpendicular from the point $P(1,-1,2)$ to the given line $\frac{x+1}{2}=\frac{y-2}{-3}=\frac{z+2}{4}$ is

The point on the line $x+y=4$ that lie at a unit distance from the line $4 x+3 y=10$ is

The area of the region bounded by the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ is

If $A(\operatorname{adj} A)=\left[\begin{array}{lll}5 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 5\end{array}\right]$, then the value of $|A|+|\operatorname{adj} A|$ is equal to :

In a kabaddi league, two matches are being played between Jaipur and Delhi. It is assumed that the outcomes of the two games are independent. The probability of Jaipur winning, drawing and losing the game against Delhi are $\frac{1}{2}, \frac{3}{10}$ and $\frac{1}{5}$ respectively. Each team gets 5 points for win, 3 points for draw and 0 points for loss in a game. After two games, find the probability that Jaipur has more points than Delhi.

$\int \frac{\sin x+\cos x}{\sqrt{1+2 \sin x \cos x}} d x=\varphi(x)+C$ Then $\varphi(x)=$

If the mean of $4,7,2,8,6$ and $k$ is 7 . Then the mean deviation from the mean of these observations is

$\int\limits_0^{\frac{\pi}{2}} \log \left(\frac{5+4 \sin x}{5+4 \cos x}\right) d x=$

The degree of the differential equation $\left[1+\left(\frac{d y}{d x}\right)^2\right]^{\frac{3}{4}}=\left(\frac{d^2 y}{d x^2}\right)^{\frac{1}{3}}$

Evaluate the value of $(1.02)^8$ using binomial theorem up to two decimal places.

$\int \frac{e^{\tan ^{-1} x}}{\left(1+x^2\right)}\left(1+x+x^2\right) d x=$

Which of the following transformations reduce the differential equation $\frac{d z}{d x}+\frac{z}{x} \log z=\frac{z}{x^2}(\log z)^2$ into the form $\frac{d u}{d x}+P(x) u=Q(x)$

The least area of a circle circumscribing any right-angle triangle of area $\frac{9}{\pi}$ sq units is

$\lim _\limits{\theta \rightarrow \frac{\pi}{2}} \frac{1-\sin \theta}{\left(\frac{\pi}{2}-\theta\right) \cos \theta}$ is equal to :

If for two events $A$ and $B, P(A-B)=\frac{1}{5}$ and $P(A)=\frac{3}{5}$ then $P(B / A)=$

$\int \frac{x}{(x-1)(x-2)^2} d x=a \log \left|\frac{x-1}{x-2}\right|+\frac{b}{(x-2)}+c$ then

The complex number $\frac{1+7 i}{(2-i)^2}$ lies in

If a function $f:[2, \infty) \rightarrow R$ defined by $f(x)=x^2-4 x+5$, then the range of $f$ is

The corner points of the feasible region determined by the system of linear constraints are $(0,3),(1,1)$ and $(3,0)$, If objective function is $Z=p x+q y, p, q>0$ then the condition on $p$ and $q$ so that the minimum of $Z$ occurs at $(3,0)$ and $(1,1)$ is

Three bags contain a number of red and white balls are as follows.

Bag I: 3 red balls

Bag II: 2 red balls and 1 white ball

Bag III: 3 White balls

The probability that bag $i$ will be chosen and a ball is selected from it is $\frac{i}{6}, i=1,2,3$. If a white ball is selected, what is the probablity that it came from Bag III

The line $A B$ passes through the point $P(-4,3)$ and the portion of the line intercepted between the axes is divided internally in the ratio $5: 3$ by the point $P$. Given that the point A lies on $x$-axis and B lies on $y$-axis, then the $x$ intercept of the line is

If $Q(1,0,1)$ is the image of the point $P(a, b, c)$ in the line $\frac{x+1}{2}=\frac{y-3}{-2}=\frac{z}{-1}$ then $a+b+c$ is equal to :

The cost of 4 kg onion, 3 kg wheat and 2 kg rice is ₹ 500 .

The cost of 1 kg onion, 2 kg wheat and 3 kg rice is ₹ 300 .

The cost of 6 kg onion, 2 kg wheat and 3 kg rice is ₹ 575 .

The above situation can be represented in matrix form as $\mathrm{AX}=\mathrm{B}$. Then $\left|5 A^{-1}\right|=$

Let $A$ and $G$ denote the arithmetic mean and geometric mean of positive real numbers $5^x$ and $5^{1-x}$. Then the minimum value of the expression $5^x+5^{1-x}$ where $x \in R$ is

In a triangle $A B C$ the coordinate of the vertex $A$ is $(1,2)$. Equations of the median through $B$ and $C$ are respectively $x+y=5$ and $x=4$. Then the equation of side $\mathbf{A B}$ is

The radius of the circle passes through the foci of a conic $\frac{x^2}{16}+\frac{y^2}{9}=1$ and has its centre at $(0,3)$, then the diameter of the circle is ---

If $A=\{1,2,4\} \quad B=\{2,4,5\} \quad C=\{2,5\}$ then $(A-B) \cap(B-C)=$

$\int \frac{d x}{x \sqrt{4 x^2-9}}=$

In the interval $(0,1)$ the function $f(x)=x^2-x+1$ is

If $|\vec{a}|=2 \sqrt{2}$ and $|\vec{b}|=3$ and angle between $\vec{a}$ and $\vec{b}$ is $\frac{\pi}{4}$. If a parallelogram is constructed with adjacent sides $\vec{p}=2 \vec{a}-3 \vec{b}$ and $\vec{q}=\vec{a}+\vec{b}$ then the product of length of both the diagonals is :

The value of $\tan ^{-1}\left(\tan \frac{7 \pi}{6}\right)$ is

The cofactor of the element $a_{21}$ in the expansion of $\Delta=\left|\begin{array}{ccc}1 & 4 & 4 \\ -3 & 5 & 9 \\ 2 & 1 & 2\end{array}\right|$ is

If for real values of $x, \cos \theta=x+\frac{1}{x}$, then $X$

Solution of the differential equation $y \frac{d y}{d x}+x=0$ represents a family of

The inequality representing the following graph is

Position vector of P and Q are $\hat{\imath}+3 \hat{\jmath}-7 \hat{k}$ and $5 \hat{\imath}-2 \hat{\jmath}+4 \hat{k}$ respectively. Then the cosine of the angle between $\overrightarrow{P Q}$ and y -axis is

Domain of the function $f(x)=\sqrt{\sin ^{-1}(2 x)+\frac{\pi}{6}}$ for real valued of $x$ is

Shortest distance between the lines $\vec{r}=(8+3 \lambda) \hat{\imath}-(9+16 \lambda) \hat{\jmath}+(10+7 \lambda) \hat{k}$ and $\vec{r}=15 \hat{\imath}+29 \hat{\jmath}+5 \hat{k}+\mu(3 \hat{\imath}+8 \hat{\jmath}-5 \hat{k})$ is

$\lim _\limits{x \rightarrow 1} \frac{(\sqrt{x}-1)(2 x-3)}{2 x^2+x-3}$ is

Physics

A circular coil of area $2 \sqrt{2} \mathrm{~cm}^2$ and resistance $2 \boldsymbol{\Omega}$ is arranged vertically in the east -west direction. A uniform magnetic field 0.2 T is set up across the plane in the north to east direction. Now the magnetic field is removed at a steady rate in 0.4 s What is the current developed in the coil?

A car, starting from rest, accelerates at the rate (f) through a distance ( $S$ ), then continues at constant speed for some time $(t)$ and then decelerates at the rate $\frac{f}{2}$ to come to rest. If the total distance is $5 S$, then

A particle ' X ' carrying a charge +Q is moving in a circular path of radius R around another particle ' Y ' having a charge -Q with a frequency ' $v$ '. Then the mass ' $m$ ' of the charged particle is

Three ideal diodes and resistors connected to the cell of negligible internal resistance is as shown. Find the current passing through the $10 \Omega$ resistor.

A coin is placed on a disc rotating with an angular velocity $\omega$. The co-efficient of friction between the disc and the coin is $\mu$. The maximum distance of the coin from the centre of the disc up to which it will rotate with the disc is

A beam of light parallel to the principal axis of a concave and convex lens, first passes through the concave lens of focal length 0.5 m and then through the convex lens of focal length 1.75 m . If the lenses are placed 1.25 apart, which of the given statement is true?

Three point charges $-1 C,+1 C,+1 C$ are placed at points $A, B, C$ respectively of a triangle $A B C$. What is the total potential energy of the system? [given $\mathrm{AB}=\mathrm{AC}=6 \mathrm{~cm}$ and $\mathrm{BC}=3 \mathrm{~cm}$ ]

When a body of refractive index $\boldsymbol{\mu}=\mathbf{1 . 4}$ is put into a liquid, the body becomes invisible. What would be the refractive index of the medium?

What is the frequency ' $\nu$ ' of the electron in Bohr's first orbit of radius ' $r$ ' of the hydrogen atom?

Water from a tap emerges vertically downwards with an initial speed of $1.0 \mathrm{~ms}^{-1}$. The cross-sectional area of the tap is $1 \mathrm{~cm}^2$. Assume that the pressure is constant throughout the stream of water and that the flow is steady. The cross-sectional area of the stream 15 cm below the tap is $\left(\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$

A bullet of momentum $p$ is fired into a door and gets embedded exactly at the center of the door. The door is 1.0 m wide and weighs 12 kg . It is hinged at one end and rotates about a vertical axis practically without friction. The angular speed of the door just after the bullet embeds into it is :

A wind mill converts a fixed fraction of the wind energy intercepted by its blades into electrical energy. The electrical power output P is related to the velocity of wind v as

The value of universal gravitational constant was first determined by

A current of 2 A is passed through the primary coil. The total flux linked with the secondary coil, which is closely wound over the primary is $2000 \times 10^{-6}$ weber. What is the induced emf in the secondary if the current through the primary increases at a rate of $0.2 \mathrm{As}^{-1}$ ?

To get 300 MW electric power for half an hour, how much mass is to be completely converted into energy?

The electric field versus distance graph is shown as given. Select the correct statement from the following.