WB JEE 2024 | WB JEE Year Wise Previous Years Questions

Chemistry

Mathematics

1. All values of a for which the inequality $$\frac{1}{\sqrt{a}} \int_\limits1^a\left(\frac{3}{2} \sqrt{x}+1-\frac{1}{\sqrt 2. For any integer $$\mathrm{n}, \int_\limits0^\pi \mathrm{e}^{\cos ^2 x} \cdot \cos ^3(2 n+1) x \mathrm{~d} x$$ has the va 3. Let $$\mathrm{f}$$ be a differential function with $$\lim _\limits{x \rightarrow \infty} \mathrm{f}(x)=0$$. If $$\mathrm 4. If $$x y^{\prime}+y-e^x=0, y(a)=b$$, then $$\lim _\limits{x \rightarrow 1} y(x)$$ is 5. The area bounded by the curves $$x=4-y^2$$ and the Y-axis is 6. $$f(x)=\cos x-1+\frac{x^2}{2!}, x \in \mathbb{R}$$ Then $$\mathrm{f}(x)$$ is 7. Let $$\mathrm{y}=\mathrm{f}(x)$$ be any curve on the $$\mathrm{X}-\mathrm{Y}$$ plane & $$\mathrm{P}$$ be a point on the 8. If a particle moves in a straight line according to the law $$x=a \sin (\sqrt{\lambda} t+b)$$, then the particle will co 9. A unit vector in XY-plane making an angle $$45^{\circ}$$ with $$\hat{i}+\hat{j}$$ and an angle $$60^{\circ}$$ with $$3 \ 10. Let $$\mathrm{f}: \mathbb{R} \rightarrow \mathbb{R}$$ be given by $$\mathrm{f}(x)=\left|x^2-1\right|$$, then 11. Given an A.P. and a G.P. with positive terms, with the first and second terms of the progressions being equal. If $$a_n$ 12. If for the series $$a_1, a_2, a_3$$, ...... etc, $$\mathrm{a}_{\mathrm{r}}-\mathrm{a}_{\mathrm{r}+\mathrm{i}}$$ bears a 13. If $$z_1$$ and $$z_2$$ be two roots of the equation $$z^2+a z+b=0, a^2 14. If $$\cos \theta+i \sin \theta, \theta \in \mathbb{R}$$, is a root of the equation $$a_0 x^n+a_1 x^{n-1}+\ldots .+a_{n-1 15. If $$\left(x^2 \log _x 27\right) \cdot \log _9 x=x+4$$ then the value of $$x$$ is 16. If $$\mathrm{P}(x)=\mathrm{a} x^2+\mathrm{b} x+\mathrm{c}$$ and $$\mathrm{Q}(x)=-\mathrm{a} x^2+\mathrm{d} x+\mathrm{c}$ 17. Let $$\mathrm{N}$$ be the number of quadratic equations with coefficients from $$\{0,1,2, \ldots, 9\}$$ such that 0 is a 18. If $$a, b, c$$ are distinct odd natural numbers, then the number of rational roots of the equation $$a x^2+b x+c=0$$ 19. The numbers $$1,2,3, \ldots \ldots, \mathrm{m}$$ are arranged in random order. The number of ways this can be done, so t 20. If $$A=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right)$$ and $$\theta=\ 21. If $$\left(1+x+x^2+x^3\right)^5=\sum_\limits{k=0}^{15} a_k x^k$$ then $$\sum_\limits{k=0}^7(-1)^{\mathbf{k}} \cdot a_{2 22. The coefficient of $$a^{10} b^7 c^3$$ in the expansion of $$(b c+c a+a b)^{10}$$ is 23. $$ \text { If }\left|\begin{array}{lll} x^k & x^{k+2} & x^{k+3} \\ y^k & y^{k+2} & y^{k+3} \\ z^k & z^{k+2} & z^{k+3} \e 24. If $$\left[\begin{array}{ll}2 & 1 \\ 3 & 2\end{array}\right] \cdot A \cdot\left[\begin{array}{cc}-3 & 2 \\ 5 & -3\end{ar 25. $$ \text { Let } f(x)=\left|\begin{array}{ccc} \cos x & x & 1 \\ 2 \sin x & x^3 & 2 x \\ \tan x & x & 1 \end{array}\righ 26. In R, a relation p is defined as follows: $$\forall a, b \in \mathbb{R}, a p$$ holds iff $$a^2-4 a b+3 b^2=0$$. Then 27. Let $$\mathrm{f}: \mathbb{R} \rightarrow \mathbb{R}$$ be a function defined by $$\mathrm{f}(x)=\frac{\mathrm{e}^{|x|}-\m 28. Let A be the set of even natural numbers that are 29. Two smallest squares are chosen one by one on a chess board. The probability that they have a side in common is 30. Two integers $$\mathrm{r}$$ and $$\mathrm{s}$$ are drawn one at a time without replacement from the set $$\{1,2, \ldots, 31. A biased coin with probability $$\mathrm{p}(0 32. The expression $$\cos ^2 \phi+\cos ^2(\theta+\phi)-2 \cos \theta \cos \phi \cos (\theta+\phi)$$ is 33. If $$0 34. The equation $$\mathrm{r} \cos \theta=2 \mathrm{a} \sin ^2 \theta$$ represents the curve 35. If $$(1,5)$$ be the midpoint of the segment of a line between the line $$5 x-y-4=0$$ and $$3 x+4 y-4=0$$, then the equat 36. In $$\triangle \mathrm{ABC}$$, co-ordinates of $$\mathrm{A}$$ are $$(1,2)$$ and the equation of the medians through $$\m 37. A line of fixed length $$\mathrm{a}+\mathrm{b} . \mathrm{a} \neq \mathrm{b}$$ moves so that its ends are always on two f 38. With origin as a focus and $$x=4$$ as corresponding directrix, a family of ellipse are drawn. Then the locus of an end o 39. Chords $$\mathrm{AB}$$ & $$\mathrm{CD}$$ of a circle intersect at right angle at the point $$\mathrm{P}$$. If the length 40. The plane $$2 x-y+3 z+5=0$$ is rotated through $$90^{\circ}$$ about its line of intersection with the plane $$x+y+z=1$$. 41. If the relation between the direction ratios of two lines in $$\mathbb{R}^3$$ are given by $$l+\mathrm{m}+\mathrm{n}=0,2 42. $$\triangle \mathrm{OAB}$$ is an equilateral triangle inscribed in the parabola $$\mathrm{y}^2=4 \mathrm{a} x, \mathrm{a 43. For every real number $$x \neq-1$$, let $$\mathrm{f}(x)=\frac{x}{x+1}$$. Write $$\mathrm{f}_1(x)=\mathrm{f}(x)$$ & for $ 44. If $$\mathrm{U}_{\mathrm{n}}(\mathrm{n}=1,2)$$ denotes the $$\mathrm{n}^{\text {th }}$$ derivative $$(\mathrm{n}=1,2)$$ 45. The equation $$2^x+5^x=3^x+4^x$$ has 46. Consider the function $$\mathrm{f}(x)=(x-2) \log _{\mathrm{e}} x$$. Then the equation $$x \log _{\mathrm{e}} x=2-x$$ 47. If $$\alpha, \beta$$ are the roots of the equation $$a x^2+b x+c=0$$ then $$\lim _\limits{x \rightarrow \beta} \frac{1-\ 48. If $$\mathrm{f}(x)=\frac{\mathrm{e}^x}{1+\mathrm{e}^x}, \mathrm{I}_1=\int_\limits{\mathrm{f}(-\mathrm{a})}^{\mathrm{f}(\ 49. Let $$f: \mathbb{R} \rightarrow \mathbb{R}$$ be a differentiable function and $$f(1)=4$$. Then the value of $$\lim _\lim 50. $$ \text { If } \int \frac{\log _e\left(x+\sqrt{1+x^2}\right)}{\sqrt{1+x^2}} \mathrm{~d} x=\mathrm{f}(\mathrm{g}(x))+\ma 51. Let $$\mathrm{I}(\mathrm{R})=\int_\limits0^{\mathrm{R}} \mathrm{e}^{-\mathrm{R} \sin x} \mathrm{~d} x, \mathrm{R}>0$$. t 52. Consider the function $$\mathrm{f}(x)=x(x-1)(x-2) \ldots(x-100)$$. Which one of the following is correct? 53. In a plane $$\vec{a}$$ and $$\vec{b}$$ are the position vectors of two points A and B respectively. A point $P$ with pos 54. Five balls of different colours are to be placed in three boxes of different sizes. The number of ways in which we can p 55. Let $$A=\left(\begin{array}{ccc}1 & -1 & 0 \\ 0 & 1 & -1 \\ 1 & 1 & 1\end{array}\right), B=\left(\begin{array}{l}2 \\ 1 56. If $$\alpha_1, \alpha_2, \ldots, \alpha_n$$ are in A.P. with common difference $$\theta$$, then the sum of the series $$ 57. For the real numbers $$x$$ & $$y$$, we write $$x$$ p y iff $$x-y+\sqrt{2}$$ is an irrational number. Then relation p is 58. Let $$A=\left[\begin{array}{ccc}0 & 0 & -1 \\ 0 & -1 & 0 \\ -1 & 0 & 0\end{array}\right]$$, then 59. $$ \text { If } 1000!=3^n \times m \text { where } m \text { is an integer not divisible by } 3 \text {, then } n= $$ 60. If $$A$$ and $$B$$ are acute angles such that $$\sin A=\sin ^2 B$$ and $$2 \cos ^2 A=3 \cos ^2 B$$, then $$(A, B)=$$ 61. If two circles which pass through the points $$(0, a)$$ and $$(0,-a)$$ and touch the line $$\mathrm{y}=\mathrm{m} x+\mat 62. The locus of the midpoint of the system of parallel chords parallel to the line $$y=2 x$$ to the hyperbola $$9 x^2-4 y^2 63. Angle between two diagonals of a cube will be 64. $$ \text { If } y=\tan ^{-1}\left[\frac{\log _e\left(\frac{e}{x^2}\right)}{\log _e\left(e x^2\right)}\right]+\tan ^{-1}\ 65. $$\lim _\limits{n \rightarrow \infty} \frac{1}{n^{k+1}}[2^k+4^k+6^k+\ldots .+(2 n)^k]=$$ 66. The acceleration f $$\mathrm{ft} / \mathrm{sec}^2$$ of a particle after a time $$\mathrm{t}$$ sec starting from rest is 67. Let $$\Gamma$$ be the curve $$\mathrm{y}=\mathrm{be}^{-x / a}$$ & $$\mathrm{L}$$ be the straight line $$\frac{x}{\mathrm 68. If $$n$$ is a positive integer, the value of $$(2 n+1){ }^n C_0+(2 n-1){ }^n C_1+(2 n-3){ }^n C_2 +\ldots .+1 \cdot{ }^n 69. If the quadratic equation $$a x^2+b x+c=0(a>0)$$ has two roots $$\alpha$$ and $$\beta$$ such that $$\alpha2$$, then 70. If $$\mathrm{a}_{\mathrm{i}}, \mathrm{b}_{\mathrm{i}}, \mathrm{c}_{\mathrm{i}} \in \mathbb{R}(\mathrm{i}=1,2,3)$$ and $$ 71. The function $$\mathrm{f}: \mathbb{R} \rightarrow \mathbb{R}$$ defined by $$\mathrm{f}(x)=\mathrm{e}^x+\mathrm{e}^{-x}$$ 72. A square with each side equal to '$$a$$' above the $$x$$-axis and has one vertex at the origin. One of the sides passing 73. If $$\mathrm{ABC}$$ is an isosceles triangle and the coordinates of the base points are $$B(1,3)$$ and $$C(-2,7)$$. The 74. $$ \text { The points of extremum of } \int_\limits0^{x^2} \frac{t^2-5 t+4}{2+e^t} d t \text { are } $$ 75. Choose the correct statement :

Physics

1. Let $$\theta$$ be the angle between two vectors $$\vec{A}$$ and $$\vec{B}$$. If $$\hat{a}_{\perp}$$ is the unit vector p 2. The Power $$(\mathrm{P})$$ radiated from an accelerated charged particle is given by $$\mathrm{P} \propto \frac{(q \math 3. Two convex lens $$(\mathrm{L}_1$$ and $$\mathrm{L}_2)$$ of equal focal length $$\mathrm{f}$$ are placed at a distance $$ 4. Which of the following quantity has the dimension of length ? (h is Planck's constant, m is the mass of electron and c i 5. The speed distribution for a sample of $$\mathrm{N}$$ gas particles is shown below. $$\mathrm{P}(\mathrm{v})=0$$ for $$\ 6. The internal energy of a thermodynamic system is given by $$U=a s^{4 / 3} V^\alpha$$ where $$\mathrm{s}$$ is entropy, $$ 7. A particle of mass '$$m$$' moves in one dimension under the action of a conservative force whose potential energy has th 8. Longitudinal waves cannot 9. A $$2 \mathrm{~V}$$ cell is connected across the points $$\mathrm{A}$$ and $$\mathrm{B}$$ as shown in the figure. Assume 10. A charge Q is placed at the centre of a cube of sides a. The total flux of electric field through the six surfaces of th 11. The elastic potential energy of a strained body is 12. Which of the following statement(s) is/are truc in respect of nuclear binding energy ? (i) The mass energy of a nucleus 13. A satellite of mass $$\mathrm{m}$$ rotates round the earth in a circular orbit of radius R. If the angular momentum of t 14. What force $$\mathrm{F}$$ is required to start moving this $$10 \mathrm{~kg}$$ block shown in the figure if it acts at a 15. Light of wavelength $$6000 \mathop A\limits^o$$ is incident on a thin glass plate of r.i. 1.5 such that the angle of ref 16. Consider a circuit where a cell of emf $$E_0$$ and internal resistance $$\mathrm{r}$$ is connected across the terminal 17. The equivalent capacitance of a combination of connected capacitors shown in the figure between the points $$\mathrm{P}$ 18. In a single-slit diffraction experiment, the slit is illuminated by light of two wavelengths $$\lambda_1$$ and $$\lambda 19. The acceleration-time graph of a particle moving in a straight line is shown in the figure. If the initial velocity of t 20. The position vector of a particle of mass $$\mathrm{m}$$ moving with a constant velocity $$\vec{v}$$ is given by $$\vec{ 21. The position of the centre of mass of the uniform plate as shown in the figure is 22. In a series LCR circuit, the rms voltage across the resistor and the capacitor are $$30 \mathrm{~V}$$ and $$90 \mathrm{ 23. A small ball of mass m is suspended from the ceiling of a floor by a string of length $$\mathrm{L}$$. The ball moves al 24. If $$\hat{n}_1, \hat{n}_2$$ and $$\hat{\mathrm{t}}$$ represent, unit vectors along the incident ray, reflected ray and n 25. A beam of light of wavelength $$\lambda$$ falls on a metal having work function $$\phi$$ placed in a magnetic field B. T 26. A charged particle moving with a velocity $$\vec{v}=v_1 \hat{i}+v_2 \hat{j}$$ in a magnetic field $$\vec{B}$$ experience 27. Two straight conducting plates form an angle $$\theta$$ where their ends are joined. A conducting bar in contact with th 28. Three point charges $$\mathrm{q},-2 \mathrm{q}$$ and $$\mathrm{q}$$ are placed along $$x$$ axis at $$x=-{a}, 0$$ and $a$ 29. A body floats with $$\frac{1}{n}$$ of its volume keeping outside of water. If the body has been taken to height $$\mathr 30. A small sphere of mass m and radius r slides down the smooth surface of a large hemispherical bowl of radius R. If the s 31. When a convex lens is placed above an empty tank, the image of a mark at the bottom of the tank, which is 45 cm from the 32. In the given network of AND and OR gates, output Q can be written as (assuming n even) 33. Water is filled in a cylindrical vessel of height $$\mathrm{H}$$. A hole is made at height $$\mathrm{z}$$ from the botto 34. A metal plate of area $$10^{-2} \mathrm{~m}^2$$ rests on a layer of castor oil, $$2 \times 10^{-3} \mathrm{~m}$$ thick, 35. The following figure shows the variation of potential energy $$V(x)$$ of a particle with distance $$x$$. The particle ha 36. Monochromatic light of wavelength $$\lambda=4770 \mathop A\limits^o $$ is incident separately on the surfaces of four di 37. Consider the integral form of the Gauss' law in electrostatics $$\oint {\overrightarrow E .d\overrightarrow S } = {Q \o 38. A uniform rod $$\mathrm{AB}$$ of length $$1 \mathrm{~m}$$ and mass $$4 \mathrm{~kg}$$ is sliding along two mutually per 39. The variation of impedance $$\mathrm{Z}$$ of a series $$\mathrm{L C R}$$ circuit with frequency of the source is shown 40. The electric field of a plane electromagnetic wave in a medium is given by $$ \overrightarrow{\mathrm{E}}(x, y, z, t)=\m

WB JEE 2024

MCQ (Single Correct Answer)

-0.25

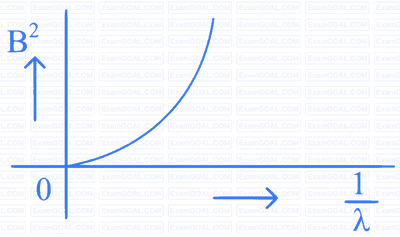
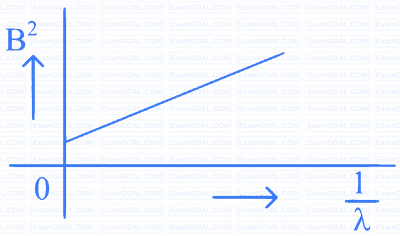
A beam of light of wavelength $$\lambda$$ falls on a metal having work function $$\phi$$ placed in a magnetic field B. The most energetic electrons, perpendicular to the field are bent in circular arcs of radius R. If the experiment is performed for different values of $$\lambda$$, then $$\mathrm{B}^2$$ vs. $$\frac{1}{\lambda}$$ graph will look like (keeping all other quantities constant)

WB JEE 2024 Physics - Dual Nature of Radiation Question 1 English Option 1

WB JEE 2024 Physics - Dual Nature of Radiation Question 1 English Option 2

WB JEE 2024

MCQ (Single Correct Answer)

-0.25

A charged particle moving with a velocity $$\vec{v}=v_1 \hat{i}+v_2 \hat{j}$$ in a magnetic field $$\vec{B}$$ experiences a force $$\vec{F}=F_1 \hat{i}+F_2 \hat{j}$$. Here $$v_1, v_2, F_1, F_2$$ all are constants. Then $$\overrightarrow{\mathrm{B}}$$ can be

$$\vec{B}=B_1 \hat{i}+B_2 \hat{j}$$ with $$\frac{v_1}{v_2}=\frac{B_1}{B_2}$$

$$\vec{B}=B_1 \hat{i}+B_2 \hat{j}+B_3 \hat{k}$$ with $$\frac{v_1}{v_2}=\frac{B_1}{B_2}$$

$$\overrightarrow{\mathrm{B}}=\mathrm{B}_3 \hat{\mathrm{j}}$$ with $$\mathrm{B}_1=\mathrm{B}_2=0$$

$$\vec{B}=B_1 \hat{j}+B_2 \hat{k}$$ with $$\frac{B_1}{B_2}=\frac{v_1}{v_2}$$

WB JEE 2024

MCQ (Single Correct Answer)

-0.25

Two straight conducting plates form an angle $$\theta$$ where their ends are joined. A conducting bar in contact with the plates and forming an isosceles triangle with them starts at the vertex at time $$t=0$$ and moves with constant velocity $$\vec{v}$$ to the right as shown in figure. A magnetic field $$\vec{B}$$ points out of the page. The magnitude of emf induced at $$t=1$$ second will be

WB JEE 2024 Physics - Electromagnetic Induction Question 1 English

$$\mathrm{Bv} \tan \frac{\theta}{2}$$

$$2 \mathrm{Bv}^2 \tan \frac{\theta}{2}$$

$$2 \mathrm{Bv}^2 \cot \frac{\theta}{2}$$

$$2 \mathrm{Bv}^2 \sin \frac{\theta}{2}$$

WB JEE 2024

MCQ (Single Correct Answer)

-0.25

Three point charges $$\mathrm{q},-2 \mathrm{q}$$ and $$\mathrm{q}$$ are placed along $$x$$ axis at $$x=-{a}, 0$$ and $a$ respectively. As $$\mathrm{a} \rightarrow 0$$ and $$\mathrm{q} \rightarrow \infty$$ while $$\mathrm{q} \mathrm{a}^2=\mathrm{Q}$$ remains finite, the electric field at a point P, at a distance $$x(x \gg a)$$ from $$x=0$$ is $$\overrightarrow{\mathrm{E}}=\frac{\alpha \mathrm{Q}}{4 \pi \epsilon_0 x^\beta} \hat{i}$$. Then

$$\alpha=\beta$$

$$\alpha=2 \beta$$

$$\alpha=\frac{2}{3} \beta$$

$$2 \alpha=3 \beta$$

PREVIOUS NEXT