WB JEE 2018
Paper was held on
Sun, Apr 22, 2018 11:00 AM
Chemistry
1
Cl2O7 is the anhydride of
2
The main reason that SiCl4 is easily hydrolysed as compared to CCl4 is that
3
Silver chloride dissolves in excess of ammonium hydroxide solution. The cation present in the resulting solution is
4
The ease of hydrolysis in the compounds CH3COCl(I), CH3 $$-$$ CO $$-$$ O $$-$$ COCH3 (II), CH3COOC2H5 (III) and CH3CONH2 (IV) is of the order
5
CH3 $$-$$ C $$ \equiv $$ C MgBr can be prepared by the reaction of
6
The number of alkene (s) which can produce 2-butanol by the successive treatment of (i) B2H6 in tetrahydrofuran solvent and (ii) alkaline H2O2 solution is
7
Identify 'M' in the following sequence of reactions


8
Methoxybenzene on treatment with HI produces
9
$$\mathop {{C_4}{H_{10}}O}\limits_{(N)} \mathop {\mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{{H_2}S{O_4}}^{{K_2}C{r_2}{O_7}}} }\limits_{} {C_4}{H_8}O\mathop {\mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{Warm}^{{I_2}/NaOH}} }\limits_{} CH{I_3}$$
Here, N is
Here, N is
10
The correct order of reactivity for the addition reaction of the following carbonyl compounds with ethylmagnesium iodide is


11
If aniline is treated with conc. H2SO4 and heated at 200$$^\circ$$C, the product is
12
Which of the following electronic configuration is not possible?
13
The number of unpaired electrons in Ni (atomic number = 28) are
14
Which of the following has the strongest H-bond?
15
The half-life of C14 is 5760 years. For a 200 mg sample of C14, the time taken to change to 25 mg is
16
Ferric ion forms a Prussian blue precipitate due to the formation of
17
The nucleus $$_{29}^{64}$$Cu accepts an orbital electron to yield,
18
How many moles of electrons will weigh one kilogram?
19
Equal weights of ethane and hydrogen are mixed in an empty container at 25$$^\circ$$C. The fraction of total pressure exerted by hydrogen is
20
The heat of neutralisation of a strong base and a strong acid is 13.7 kcal. The heat released when 0.6 mole HCl solution is added to 0.25 mole of NaOH is
21
A compound formed by elements X and Y crystallises in the cubic structure, where X atoms are at the corners of a cube and Y atoms are at the centre of the body. The formula of the compounds is
22
What amount of electricity can deposit 1 mole of Al metal at cathode when passed through molten AlCl3 ?
23
Given the standard half-cell potentials (E$$^\circ$$) of the following as
$$\matrix{ {Zn \to Z{n^{2 + }} + 2{e^ - };} & {{E^o} = + 0.76V} \cr {Fe \to F{e^{2 + }} + 2{e^ - };} & {{E^o} = 0.41V} \cr } $$
Then the standard e.m.f. of the cell with the reaction $$F{e^{2 + }} + Zn \to Z{n^{2 + }} + Fe$$ is
$$\matrix{ {Zn \to Z{n^{2 + }} + 2{e^ - };} & {{E^o} = + 0.76V} \cr {Fe \to F{e^{2 + }} + 2{e^ - };} & {{E^o} = 0.41V} \cr } $$
Then the standard e.m.f. of the cell with the reaction $$F{e^{2 + }} + Zn \to Z{n^{2 + }} + Fe$$ is
24
The following equilibrium constants are given
$${N_2} + 3{H_2}$$ $$\rightleftharpoons$$ $$2N{H_3}$$; $${K_1}$$
$${N_2} + {O_2}$$ $$\rightleftharpoons$$ $$2NO$$; $${K_2}$$
$${H_2} + {1 \over 2}{O_2}$$ $$\rightleftharpoons$$ $${H_2}O$$; $${K_3}$$
The equilibrium constant for the oxidation of 2 mole of NH3 to give NO is
$${N_2} + 3{H_2}$$ $$\rightleftharpoons$$ $$2N{H_3}$$; $${K_1}$$
$${N_2} + {O_2}$$ $$\rightleftharpoons$$ $$2NO$$; $${K_2}$$
$${H_2} + {1 \over 2}{O_2}$$ $$\rightleftharpoons$$ $${H_2}O$$; $${K_3}$$
The equilibrium constant for the oxidation of 2 mole of NH3 to give NO is
25
Which one of the following is a condensation polymer?
26
Which of the following is present in maximum amount in 'acid rain'?
27
Which of the set of oxides are arranged in the proper order of basic, amphoteric, acidic?
28
Out of the following outer electronic configurations of atoms, the highest oxidation state is achieved by which one?
29
At room temperature, the reaction between water and fluorine produces
30
Which of the following is least thermally stable?
31
$$[P]\buildrel {B{r_2}} \over
\longrightarrow {C_2}{H_4}B{r_2}\mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{N{H_3}}^{NaN{H_2}}} [Q]$$
$$[Q]\mathrel{\mathop{\kern0pt\longrightarrow} \limits_{H{g^{2 + }},\Delta }^{20\% /{H_2}S{O_4}}} [R]\buildrel {Zn - Hg/HCl} \over \longrightarrow [S]$$
The species P, Q, R and S respectively are
$$[Q]\mathrel{\mathop{\kern0pt\longrightarrow} \limits_{H{g^{2 + }},\Delta }^{20\% /{H_2}S{O_4}}} [R]\buildrel {Zn - Hg/HCl} \over \longrightarrow [S]$$
The species P, Q, R and S respectively are
32
The number of possible organobromine compounds which can be obtained in the allylic bromination of 1-butene with N-bromosuccinimide is
33
A metal M (specific heat 0.16) forms a metal chloride with 65% chlorine present in it. The formula of the metal chloride will be
34
During a reversible adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio $${{{C_p}} \over {{C_v}}}$$ for the gas is
35
$$[X] + Dil.\,{H_2}S{O_4} \to [Y]:$$ Colourless, suffocating gas
$$[Y] + {K_2}C{r_2}{O_7} + {H_2}S{O_4} \to $$ Green colouration of solution.
Then, [X] and [Y] are
$$[Y] + {K_2}C{r_2}{O_7} + {H_2}S{O_4} \to $$ Green colouration of solution.
Then, [X] and [Y] are
36
The possible product(s) to be obtained from the reaction of cyclobutyl amine with HNO2 is/are
37
The major products obtained in the following reaction is/are
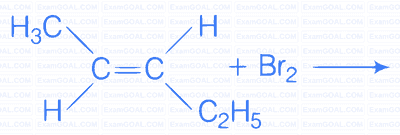

38
Which statements are correct for the peroxide ion?
39
Among the following, the extensive variables are
40
White phosphorus P4 has the following characteristics
Mathematics
1
The approximate value of sin31$$^\circ$$ is
2
Let $${f_1}(x) = {e^x}$$, $${f_2}(x) = {e^{{f_1}(x)}}$$, ......, $${f_{n + 1}}(x) = {e^{{f_n}(x)}}$$ for all n $$ \ge $$ 1. Then for any fixed n, $${d \over {dx}}{f_n}(x)$$ is
3
The domain of definition of $$f(x) = \sqrt {{{1 - |x|} \over {2 - |x|}}} $$ is
4
Let f : [a, b] $$ \to $$ R be differentiable on [a, b] and k $$ \in $$ R. Let f(a) = 0 = f(b). Also let J(x) = f'(x) + kf(x). Then
5
Let $$f(x) = 3{x^{10}} - 7{x^8} + 5{x^6} - 21{x^3} + 3{x^2} - 7$$.
Then $$\mathop {\lim }\limits_{h \to 0} {{f(1 - h) - f(1)} \over {{h^3} + 3h}}$$
Then $$\mathop {\lim }\limits_{h \to 0} {{f(1 - h) - f(1)} \over {{h^3} + 3h}}$$
6
Let f : [a, b] $$ \to $$ R be such that f is differentiable in (a, b), f is continuous at x = a and x = b and moreover f(a) = 0 = f(b). Then
7
Let f : R $$ \to $$ R be a twice continuously differentiable function such that f(0) = f(1) = f'(0) = 0. Then
8
If $$\int {{e^{\sin x}}} .\left[ {{{x{{\cos }^3}x - \sin x} \over {{{\cos }^2}x}}} \right]dx = {e^{\sin x}}f(x) + c$$, where c is constant of integration, then f(x) is equal to
9
If $$\int {f(x)} \sin x\cos xdx = {1 \over {2({b^2} - {a^2})}}\log (f(x)) + c$$, where c is the constant of integration, then f(x) is equal to
10
If $$M = \int\limits_0^{\pi /2} {{{\cos x} \over {x + 2}}dx} $$, $$N = \int\limits_0^{\pi /4} {{{\sin x\cos x} \over {{{(x + 1)}^2}}}dx} $$, then the value of M $$-$$ N is
11
The value of the integral $$I = \int_{1/2014}^{2014} {{{{{\tan }^{ - 1}}x} \over x}} dx$$ is
12
Let $$I = \int\limits_{\pi /4}^{\pi /3} {{{\sin x} \over x}} dx$$. Then
13
The value of
$$I = \int_{\pi /2}^{5\pi /2} {{{{e^{{{\tan }^{ - 1}}(\sin x)}}} \over {{e^{{{\tan }^{ - 1}}(\sin x)}} + {e^{{{\tan }^{ - 1}}(\cos x)}}}}} dx$$, is
$$I = \int_{\pi /2}^{5\pi /2} {{{{e^{{{\tan }^{ - 1}}(\sin x)}}} \over {{e^{{{\tan }^{ - 1}}(\sin x)}} + {e^{{{\tan }^{ - 1}}(\cos x)}}}}} dx$$, is
14
The value of
$$\mathop {\lim }\limits_{n \to \infty } {1 \over n}\left\{ {{{\sec }^2}{\pi \over {4n}} + {{\sec }^2}{{2\pi } \over {4n}} + ... + {{\sec }^2}{{n\pi } \over {4n}}} \right\}$$ is
$$\mathop {\lim }\limits_{n \to \infty } {1 \over n}\left\{ {{{\sec }^2}{\pi \over {4n}} + {{\sec }^2}{{2\pi } \over {4n}} + ... + {{\sec }^2}{{n\pi } \over {4n}}} \right\}$$ is
15
The differential equation representing the family of curves $${y^2} = 2d(x + \sqrt d )$$, where d is a parameter, is of
16
Let y(x) be a solution of
$$(1 + {x^2}){{dy} \over {dx}} + 2xy - 4{x^2} = 0$$. Then y(1) is equal to
$$(1 + {x^2}){{dy} \over {dx}} + 2xy - 4{x^2} = 0$$. Then y(1) is equal to
17
The law of motion of a body moving along a straight line is x = $${1 \over 2}$$ vt. x being its distance from a fixed point on the line at time t and v is its velocity there. Then
18
Number of common tangents of y = x2 and y = $$-$$x2 + 4x $$-$$ 4 is
19
Given that n numbers of arithmetic means are inserted between two sets of numbers a, 2b and 2a, b where a, b $$ \in $$ R. Suppose further that the mth means between these sets of numbers are same, then the ratio a : b equals
20
If $$x + {\log _{10}}(1 + {2^x}) = x{\log _{10}}5 + {\log _{10}}6$$, then the value of x is
21
If $${Z_r} = \sin {{2\pi r} \over {11}} - i\cos {{2\pi r} \over {11}}$$, then $$\sum\limits_{r = 0}^{10} {{Z_r}} $$ is equal to
22
If z1 and z2 be two non-zero complex numbers such that $${{{z_1}} \over {{z_2}}} + {{{z_2}} \over {{z_1}}} = 1$$, then the origin and the points represented by z1 and z2
23
If $${b_1}{b_2} = 2({c_1} + {c_2})$$ and b1, b2, c1, c2 are all real numbers, then at least one of the equations $${x^2} + {b_1}x + {c_1} = 0$$ and $${x^2} + {b_2}x + {c_2} = 0$$ has
24
The number of selection of n objects from 2n objects of which n are identical and the rest are different, is
25
If (2 $$ \le $$ r $$ \le $$ n), then $${}^n{C_r}$$ + 2 . $${}^n{C_{r + 1}}$$ + $${}^n{C_{r + 2}}$$ is equal to
26
The number (101)100 $$-$$ 1 is divisible by
27
If n is even positive integer, then the condition that the greatest term in the expansion of (1 + x)n may also have the greatest coefficient, is
28
If $$\left| {\matrix{
{ - 1} & 7 & 0 \cr
2 & 1 & { - 3} \cr
3 & 4 & 1 \cr
} } \right| = A$$, then $$\left| {\matrix{
{13} & { - 11} & 5 \cr
{ - 7} & { - 1} & {25} \cr
{ - 21} & { - 3} & { - 15} \cr
} } \right|$$ is
29
If $${a_r} = {(\cos 2r\pi + i\sin 2r\pi )^{1/9}}$$,
then the value of $$\left| {\matrix{ {{a_1}} & {{a_2}} & {{a_3}} \cr {{a_4}} & {{a_5}} & {{a_6}} \cr {{a_7}} & {{a_8}} & {{a_9}} \cr } } \right|$$ is equal to
then the value of $$\left| {\matrix{ {{a_1}} & {{a_2}} & {{a_3}} \cr {{a_4}} & {{a_5}} & {{a_6}} \cr {{a_7}} & {{a_8}} & {{a_9}} \cr } } \right|$$ is equal to
30
If $${S_r} = \left| {\matrix{
{2r} & x & {n(n + 1)} \cr
{6{r^2} - 1} & y & {{n^2}(2n + 3)} \cr
{4{r^3} - 2nr} & z & {{n^3}(n + 1)} \cr
} } \right|$$, then the value of
$$\sum\limits_{r = 1}^n {{S_r}} $$ is independent of
$$\sum\limits_{r = 1}^n {{S_r}} $$ is independent of
31
If the following three linear equations have a non-trivial solution, then
x + 4ay + az = 0
x + 3by + bz = 0
x + 2cy + cz = 0
x + 4ay + az = 0
x + 3by + bz = 0
x + 2cy + cz = 0
32
On R, a relation $$\rho $$ is defined by x$$\rho $$y if and only if x $$-$$ y is zero or irrational. Then,
33
On the set R of real numbers, the relation $$\rho $$ is defined by x$$\rho $$y, (x, y) $$ \in $$ R.
34
If f : R $$ \to $$ R be defined by f (x) = ex and g : R $$ \to $$ R be defined by g(x) = x2. The mapping gof : R $$ \to $$ R be defined by (gof) (x) = g[f(x)] $$\forall $$x$$ \in $$R. Then,
35
In order to get a head at least once with probability $$ \ge $$ 0.9, the minimum number of times a unbiased coin needs to be tossed is
36
A student appears for tests I, II and III. The student is successful if he passes in tests I, II or I, III. The probabilities of the student passing in tests I, II and III are respectively p, q and 1/2. If the probability of the student to be successful is 1/2. Then
37
If sin6$$\theta$$ + sin4$$\theta$$ + sin2$$\theta$$ = 0, then general value of $$\theta$$ is
38
If $$0 \le A \le {\pi \over 4}$$, then $${\tan ^{ - 1}}\left( {{1 \over 2}\tan 2A} \right) + {\tan ^{ - 1}}(\cot A) + {\tan ^{ - 1}}({\cot ^3}A)$$
39
Without changing the direction of the axes, the origin is transferred to the point (2, 3). Then the equation x2 + y2 $$-$$ 4x $$-$$ 6y + 9 = 0 changes to
40
The angle between a pair of tangents drawn from a point P to the circle x2 + y2 + 4x $$-$$ 6y + 9sin2$$\alpha$$ + 13cos2$$\alpha$$ = 0 is 2$$\alpha$$. The equation of the locus of the point P is
41
The point Q is the image of the point P(1, 5) about the line y = x and R is the image of the point Q about the line y = $$-$$ X. The circumcentre of the $$\Delta$$PQR is
42
The angular points of a triangle are A($$-$$ 1, $$-$$ 7), B(5, 1) and C(1, 4). The equation of the bisector of the angle $$\angle $$ABC is
43
If one of the diameter of the circle, given by the equation x2 + y2 + 4x + 6y $$-$$ 12 = 0, is a chord of a circle S, whose centre is (2, $$-$$ 3), the radius of S is
44
A chord AB is drawn from the point A(0, 3) on the circle x2 + 4x + (y $$-$$ 3)2 = 0, and is extended to M such that AM = 2AB. The locus of M is
45
Let the eccentricity of the hyperbola $${{{x^2}} \over {{a^2}}} - {{{y^2}} \over {{b^2}}} = 1$$ be reciprocal to that of the ellipse x2 + 9y2 = 9, then the ratio of a2 : b2 equals to
46
Let A, B the two distinct points on the parabola y2 = 4x. If the axis of the parabola touches a circle of radius r having AB as diameter, the slope of the line AB is
47
Let P(at2, 2at), Q, R(ar2, 2ar) be three points on a parabola y2 = 4ax. If PQ is the focal chord and PK, QR are parallel where the co-ordinates of K is (2a, 0), then the value of r is
48
Let P be a point on the ellipse $${{{x^2}} \over 9} + {{{y^2}} \over 4} = 1$$ and the line through P parallel to the Y-axis meets the circle x2 + y2 = 9 at Q, where P, Q are on the same side of the X-axis. If R is a point on PQ such that $${{PR} \over {RQ}} = {1 \over 2}$$, then the locus of R is
49
A point P lies on a line through Q(1, $$-$$2, 3) and is parallel to the line $${x \over 1} = {y \over 4} = {z \over 5}$$. If P lies on the plane 2x + 3y $$-$$ 4z + 22 = 0, then segment PQ equals
50
The foot of the perpendicular drawn from the point (1, 8, 4) on the line joining the point (0, $$-$$11, 4) and (2, $$-$$3, 1) is
51
A ladder 20 ft long leans against a vertical wall. The top end slides downwards at the rate of 2 ft per second. The rate at which the lower end moves on a horizontal floor when it is 12 ft from the wall is
52
For 0 $$ \le $$ p $$ \le $$ 1 and for any positive a, b; let I(p) = (a + b)p, J(p) = ap + bp, then
53
Let $$\overrightarrow \alpha $$ = $$\widehat i + \widehat j + \widehat k$$, $$\overrightarrow \beta $$ = $$\widehat i - \widehat j - \widehat k$$ and $${\overrightarrow \gamma }$$ = $$ - \widehat i - \widehat j - \widehat k$$ be three vectors. A vector $$\overrightarrow \delta $$, in the plane of $$\overrightarrow \alpha $$ and $$\overrightarrow \beta $$, whose projection on $${\overrightarrow \gamma }$$ is $${1 \over {\sqrt 3 }}$$, is given by
54
Let $$\overrightarrow \alpha $$, $${\overrightarrow \beta }$$, $${\overrightarrow \gamma }$$ be the three unit vectors such that $$\overrightarrow \alpha .\overrightarrow \beta = \overrightarrow \alpha .\overrightarrow \gamma = 0$$ and the angle between $$\overrightarrow \beta $$ and $$\overrightarrow \gamma $$ is 30$$^\circ$$. Then $$\overrightarrow \alpha $$ is
55
Let z1 and z2 be complex numbers such that z1 $$ \ne $$ z2 and |z1| = |z2|. If Re(z1) > 0 and Im(z2) < 0, then $${{{z_1} + {z_2}} \over {{z_1} - {z_2}}}$$ is
56
From a collection of 20 consecutive natural numbers, four are selected such that they are not consecutive. The number of such selections is
57
The least positive integer n such that $${\left( {\matrix{
{\cos \pi /4} & {\sin \pi /4} \cr
{ - \sin {\pi \over 4}} & {\cos {\pi \over 4}} \cr
} } \right)^n}$$ is an identity matrix of order 2 is
58
Let $$\rho $$ be a relation defined on N, the set of natural numbers, as
$$\rho $$ = {(x, y) $$ \in $$ N $$ \times $$ N : 2x + y = 41}. Then
$$\rho $$ = {(x, y) $$ \in $$ N $$ \times $$ N : 2x + y = 41}. Then
59
If the polynomial $$f(x) = \left| {\matrix{
{{{(1 + x)}^a}} & {{{(2 + x)}^b}} & 1 \cr
1 & {{{(1 + x)}^a}} & {{{(2 + x)}^b}} \cr
{{{(2 + x)}^b}} & 1 & {{{(1 + x)}^a}} \cr
} } \right|$$, then the constant term of f(x) is
60
A line cuts the X-axis at A(5, 0) and the Y-axis at B(0, $$-$$3). A variable line PQ is drawn perpendicular to AB cutting the X-axis at P and the Y-axis at Q. If AQ and BP meet at R, then the locus of R is
61
Let A be the centre of the circle $${x^2} + {y^2} - 2x - 4y - 20 = 0$$. Let B(1, 7) and D(4, $$-$$2) be two points on the circle such that tangents at B and D meet at C. The area of the quadrilateral ABCD is
62
Let $$f(x) = \left\{ {\matrix{
{ - 2\sin x,} & {if\,x \le - {\pi \over 2}} \cr
{A\sin x + B,} & {if\, - {\pi \over 2} < x < {\pi \over 2}} \cr
{\cos x} & {if\,x \ge {\pi \over 2}} \cr
} } \right.$$. Then,
63
The normal to the curve $$y = {x^2} - x + 1$$, drawn at the points with the abscissa $${x_1} = 0$$, $${x_2} = - 1$$ and $${x_3} = {5 \over 2}$$
64
The equation x log x = 3 $$-$$ x
65
Consider the parabola y2 = 4x. Let P and Q be points on the parabola where P(4, $$-$$ 4) and Q(9, 6). Let R be a point on the arc of the parabola between P and Q. Then, the area of $$\Delta$$PQR is largest when
66
Let $$I = \int\limits_0^I {{{{x^3}\cos 3x} \over {2 + {x^2}}}dx} $$, then
67
A particle is in motion along a curve 12y = x3. The rate of change of its ordinate exceeds that of abscissa in
68
The area of the region lying above X-axis, and included between the circle x2 + y2 = 2ax and the parabola y2 = ax, a > 0 is
69
If the equation $${x^2} - cx + d = 0$$ has roots equal to the fourth powers of the roots of $${x^2} + ax + b = 0$$, where $${a^2} > 4b$$, then the roots of $${x^2} - 4bx + 2{b^2} - c = 0$$ will be
70
On the occasion of Dipawali festival each student of a class sends greeting cards to others. If there are 20 students in the class, the number of cards sends by students is
71
In a third order matrix A, aij denotes the element in the ith row and jth column. If aij = 0 for i = j
= 1 for i > j
= $$-$$ 1 for i < j
Then the matrix is
= 1 for i > j
= $$-$$ 1 for i < j
Then the matrix is
72
The area of the triangle formed by the intersection of a line parallel to X-axis and passing through P(h, k), with the lines y = x and x + y = 2 is h2. The locus of the point P is
73
A hyperbola, having the transverse axis of length 2sin$$\theta$$ is confocal wit6h the ellipse 3x2 + 4y2 = 12. Its equation is
74
Let $$f(x) = \cos \left( {{\pi \over x}} \right),x \ne 0$$, then assuming k as an integer,
75
Consider the function $$y = {\log _a}(x + \sqrt {{x^2} + 1} ),a > 0,a \ne 1$$. The inverse of the function
Physics
1
Four resistors, 100$$\Omega $$, 200$$\Omega $$, 300$$\Omega $$ and 400$$\Omega $$ are connected to form four sides of a square. The resistors can be connected in any order. What is the maximum possible equivalent resistance across the diagonal of the square?
2
What will be current through the 200$$\Omega $$ resistor in the given circuit, a long time after the switch K is made on?


3
A point source is placed at coordinates (0, 1) in xy-plane. A ray of light from the source is reflected on a plane mirror placed along the X-axis and perpendicular to the xy-plane. The reflected ray passes through the point (3, 3). What is the path length of the ray from (0, 1) to (3, 3)?
4

Two identical equiconvex lenses, each of focal length f are placed side by side in contact with each other with a layer of water in between them as shown in the figure. If refractive index of the material of the lenses is greater than that of water, how the combined focal length F is related to f?
5
There is a small air bubble at the centre of a solid glass sphere of radius r and refractive index $$\mu$$. What will be the apparent distance of the bubble from the centre of the sphere, when viewed from outside?
6
If Young's double slit experiment is done with white light, which of the following statements will be true?
7
How the linear velocity v of an electron in the Bohr orbit is related to its quantum number n?
8
If the half-life of a radioactive nucleus is 3 days, nearly what fraction of the initial number of nuclei will decay on the third day? (Given, $$\root 3 \of {0.25} \approx 0.63$$)
9
An electron accelerated through a potential of 10000 V from rest has a de-Broglie wave length $$\lambda$$. What should be the accelerating potential, so that the wavelength is doubled?
10
In the circuit shown, inputs A and B are in states 1 and 0 respectively. What is the only possible stable state of the outputs X and Y?


11
What will be the current flowing through the 6k$$\Omega $$ resistor in the circuit shown, where the breakdown voltage of the Zener is 6V?


12
In case of a simple harmonic motion, if the velocity is plotted along the X-axis and the displacement (from the equilibrium position) is plotted along the Y-axis, the resultant curve happens to be an ellipse with the ratio $${{major\,axis\,(along\,X)} \over {minor\,axis\,(along\,Y)}} = 20\pi $$
What is the frequency of the simple harmonic motion?
What is the frequency of the simple harmonic motion?
13
A block of mass m2 is placed on a horizontal table and another block of mass m1 is placed on top of it. An increasing horizontal force F = at is exerted on the upper block but the lower block never moves as a result. If the coefficient of friction between the blocks is $$\mu$$1 and that between the lower block and the table is $$\mu$$2, then what is the maximum possible value of $$\mu$$1 / $$\mu$$2 ?
14
In a triangle ABC, the sides AB and AC are represented by the vectors $$3\widehat i + \widehat j + \widehat k$$ and $$\widehat i + 2\widehat j + \widehat k$$, respectively. Calculate the angle $$\angle ABC$$.
15
The velocity (v) of a particle (under a force F) depends on its distance (x) from the origin (with x > 0) $$v \propto {1 \over {\sqrt x }}$$. Find how the magnitude of the force (F) on the particle depends on x?
16
The ratio of accelerations due to gravity g1 : g2 on the surfaces of two planets is 5 : 2 and the ratio of their respective average densities $${{\rho _1}}$$ : $${{\rho _2}}$$ is 2 : 1. What is the ratio of respective escape velocities v1 : v2 from the surface of the planets?
17
A spherical liquid drop is placed on a horizontal plane. A small distance causes the volume of the drop to oscillate. The time period of oscillation (T) of the liquid drop depends on radius (r) of the drop, density ($$\rho $$) and surface tension (S) of th liquid. Which among the following will be a possible expression for T (where, k is a dimensionless constant)?
18
The stress along the length of a rod (with rectangular cross-section) is 1% of the Young's modulus of its material. What is the approximate percentage of change of its volume? (Poisson's ratio of the material of the rod is 0.3).
19
What will be the approximate terminal velocity of a rain drop of diameter $${1.8 \times {{10}^{ - 3}}}$$ m, when density of rain water $$ \approx $$ $${1.8 \times {{10}^{ - 5}}}$$ N-sm$$-$$2 (Neglect buoyancy of air)
20
The water equivalent of a calorimeter is 10 g and it contains 50 g of water at 15$$^\circ$$C. Some amount of ice, initially at $$-$$ 10$$^\circ$$C is dropped in it and half of the ice melts till equilibrium is reached. What was the initial amount of ice that was dropped (when specific heat of ice = 0.5 cal gm$$-$$1 $$^\circ$$C$$-$$1, specific heat of water = 10 cal gm$$-$$1 $$^\circ$$C$$-$$1 and latent heat of melting of ice = 80 cal gm$$-$$1) ?
21
One mole of a monoatomic ideal gas undergoes a quasistatic process, which is depicted by a straight line joining points $$({V_0},{T_0})$$ and $$({2V_0},{3T_0})$$ in a V-T diagram. What is the value of the heat capacity of the gas at the point $$({V_0},{T_0})$$?
22
For an ideal gas with initial pressure and volume pi and Vi respectively, a reversible isothermal expansion happens, when its volume becomes V0. Then, it is compressed to its original volume Vi by a reversible adiabatic process. If the final pressure is pf, then which of the following statement(s) is/are true?
23
A point charge $$-$$ q is carried from a point A to another point B on the axis of a charged ring of radius r carrying a charge + q. If the point A is at a distance $${4 \over 3}r$$ from the centre of the ring and the point B is $${3 \over 4}r$$ from the centre but on the opposite side, what is the net work that need to be done for this?
24
Consider a region in free space bounded by the surfaces of an imaginary cube having sides of length a as shown in the figure. A charge + Q is placed at the centre O of the cube. P is such a point outside the cube that the line OP perpendicularly intersects the surface ABCD at R and also OR = RP = a/2. A charge + Q is placed at point P also. What is the total electric flux through the five faces of the cube other than ABCD?


25
Four equal charges of value + Q are placed at any four vertices of a regular hexagon of side 'a'. By suitably choosing the vertices, what can be maximum possible magnitude of electric field at the centre of the hexagon?
26
A proton of mass m moving with a speed v (< < c, velocity of light in vacuum) completes a circular orbit in time T in a uniform magnetic field. If the speed of the proton is increased to $$\sqrt 2 $$ v, what will be time needed to complete the circular orbit?
27
A uniform current is flowing along the length of an infinite, straight, thin, hollow cylinder of radius R. The magnetic field B produced at a perpendicular distance d from the axis of the cylinder is plotted in a graph. Which of the following figures looks like the plot?
28
A circular loop of radius r of conducting wire connected with a voltage source of zero internal resistance produces a magnetic field B at its centre. If instead, a circular loop of radius 2r, made of same material, having the same cross-section is connected to the same voltage source, what will be the magnetic field at its centre?
29
An alternating current is flowing through a series L-C-R circuit. It is found that the current reaches a value of 1 mA at both 200 Hz and 800 Hz frequency. What is the resonance frequency of the circuit?
30
An electric bulb, a capacitor, a battery and a switch are all in series in a circuit. How does the intensity of light vary when the switch is turn on?
31
A light charged particle is revolving in a circle of radius r in electrostatic attraction of a static heavy particle with opposite charge. How does the magnetic field B at the centre of the circle due to the moving charge depend on r?
32
As shown in the figure, a rectangular loop of conducting wire is moving away with a constant velocity v in a perpendicular direction from a very long straight conductor carrying a steady current I. When the breadth of the rectangular loop is very small compared to its distance from the straight conductor, how does the emf. E induced in the loop vary with time t?


33
A solid spherical ball and a hollow spherical ball of two different materials of densities $$\rho $$1 and $$\rho $$2 respectively have same outer radii and same mass. What will be the ratio, the moment of inertia (about an axis passing through the centre) of the hollow sphere to that of the solid sphere?
34
The insulated plates of a charged parallel plate capacitor (with small separation between the plates) are approaching each other due to electrostatic attraction. Assuming no other force to be operative and no radiation taking place, which of the following graphs approximately shows the variation with time (t) of the potential difference (V) between the plates?
35
The bob of a pendulum of mass m, suspended by an inextensible string of length L as shown in the figure carries a small charge q. An infinite horizontal plane conductor with uniform surface charge density $$\sigma$$ is placed below it. What will be the time period of the pendulum for small amplitude oscillations?


36
A non-zero current passes through the galvanometer G shown in the circuit when the key K is closed and its value does not change when the key is opened. Then, which of the following statement(s) is/are true?


37

A ray of light is incident on a right angled isosceles prism parallel to its base as shown in the figure. Refractive index of the material of the prism is $$\sqrt 2 $$. Then, which of the following statement(s) is/are true?
38
The intensity of a sound appears to an observer to be periodic. Which of the following can be the cause of it?
39
Which of the following statement(s) is/are true?
"Internal energy of an ideal gas .............."
"Internal energy of an ideal gas .............."
40
Two positive charges Q and 4Q are placed at points A and B respectively, where B is at a distance d units to the right of A. The total electric potential due to these charges is minimum at P on the line through A and B. What is (are) the distance (s) of P from A?