The running time of an algorithm is represented by the following recurrence relation:
$$T(n) = \begin{cases} n & n \leq 3 \\ T(\frac{n}{3})+cn & \text{ otherwise } \end{cases}$$
Which one of the following represents the time complexity of the algorithm?

In quick sort, for sorting n elements, the (n/4)th smallest element is selected as pivot using an O(n) time algorithm. What is the worst case time complexity of the quick sort?

Consider the following graph: 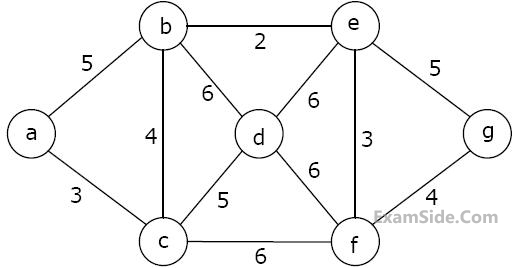Which one of the following is NOT the sequence of edges added to the minimum spanning tree using Kruskal’s algorithm?

A sub-sequence of a given sequence is just the given sequence with some elements (possibly none or all) left out. We are given two sequences X[m] and Y[n] of lengths m and n, respectively with indexes of X and Y starting from 0.

We wish to find the length of the longest common sub-sequence (LCS) of X[m] and Y[n] as l(m,n), where an incomplete recursive definition for the function I(i,j) to compute the length of the LCS of X[m] and Y[n] is given below:

l(i,j)  = 0, if either i = 0 or j = 0
        = expr1, if i,j > 0 and X[i-1] = Y[j-1]
        = expr2, if i,j > 0 and X[i-1] ≠ Y[j-1]

The value of l(i, j) could be obtained by dynamic programming based on the correct recursive definition of l(i, j) of the form given above, using an array L[M, N], where M = m+1 and N = n + 1, such that L[i, j] = l(i, j).

Which one of the following statements would be TRUE regarding the dynamic programming solution for the recursive definition of l(i, j)?