The magnetic field at the origin due to a current element $$i d \mathbf{l}$$ placed at a point with vector position $$\mathrm{r}$$ is

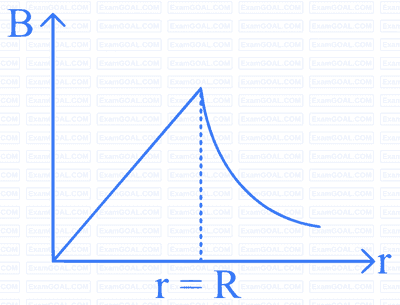
A long cylindrical wire of radius $$R$$ carries a uniform current $$I$$ flowing through it. The variation of magnetic field with distance $$r$$ from the axis of the wire is shown by

A cyclotron is used to accelerate protons $$\left({ }_1^l \mathrm{H}\right)$$ deuterons $$\left({ }_1^2 \mathrm{H}\right)$$ and $$\alpha$$-particles $$\left({ }_2^4 \mathrm{He}\right)$$. While exiting under similar conditions, the minimum $$\mathrm{KE}$$ is gained by

The ratio of magnetic field at the centre of a current carrying circular coil to its magnetic moment is $$x$$, if the current and the radius both are doubled. The new ratio will become