
A mouse of mass m jumps on the outside edge of a rotating ceiling fan of moment of inertia I and radius R. The fractional loss of angular velocity of the fan as a result is,

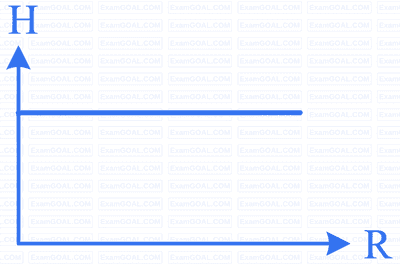
Acceleration due to gravity at a height H from the surface of a planet is the same as that at a depth of H below the surface. If R be the radius of the planet, then H vs. R graph for different planets will be,




A uniform rope of length 4 m and mass 0.4 kg is held on a frictionless table in such a way that 0.6 m of the rope is hanging over the edge. The work done to pull the hanging part of the rope on to the table is, (Assume g = 10 m/s$$^2$$)

The displacement of a plane progressive wave in a medium, travelling towards positive x-axis with velocity 4 m/s at t = 0 is given by $$y = 3\sin 2\pi \left( { - {x \over 3}} \right)$$. Then the expression for the displacement at a later time t = 4 sec will be