Chemistry
Consider the following.
I. The electron spin quantum number describes the orientation of the spin of the nucleus with respect to the magnetic field.
II. The orbitals represented by the quantum numbers $n=3, l=2, m=+2$ and $n=3, l=2, m=-2$ have the same energy.
III. The energy of a photon is directly proportional to wavelength but inversely proportional to wave number.
IV. Lyman series of lines appear in ultra-violet region.
The correct statements are
In which of the following options, the elements are correctly arranged with respect to their negative electron gain enthalpies?
Identify the option in which the molecules are arranged in the correct order of their dipole moments
The bond order of $\mathrm{O}_2^{+}$is $x$. The bond orders of $\mathrm{O}_2^{-}$and $\mathrm{O}_2^{2+}$ are respectively
Certain volume of oxygen gas diffuses through a porous pot in 20 seconds. Same volume of another gas, $X$ diffuses in $Y$ seconds as that of oxygen, then $X$ and $Y$ respectively are
Which of the following is only a redox reaction but not a disproportionation reaction?
The enthalpies of formation of gaseous $\mathrm{N}_2 \mathrm{O}$ and NO at 298 K are 82.0 and $90.0 \mathrm{~kJ} \mathrm{~mol}^{-1}$ respectively. The enthalpy change of the reaction
$\mathrm{N}_2 \mathrm{O}(g)+\frac{1}{2} \mathrm{O}_2(g) \longrightarrow 2 \mathrm{NO}(g)$ is
At 780 K and 10 atmosphere pressure the equilibrium constant for the reaction $2 A(g) \rightleftharpoons B(g)+C(g)$ is 3.52 . At the same temperature and 7.04 atmosphere pressure, the equilibrium constant for the same reaction is
The chemical name of calgon is
Which of the following set of metals have strong tendency to form super oxides?
Identify the correct statements with respect to compounds of beryllium.
I. Beryllium oxide is amphoteric in nature.
II. Beryllium hydride is formed by the reaction of beryllium with hydrogen.
III. Beryllium hydride is formed by the reaction of beryllium chloride with lithium aluminium hydride.
IV. Beryllium sulpahte is the least soluble sulphate among the sulphates of alkaline earth metals.
In group 13 of the long form of periodic table an element $X$ has a boiling point of $T_2(\mathrm{~K})$ and melting point of $T_1(\mathrm{~K})$. Identify the element $X$ for which $T_2-T_1(\mathrm{~K})$ is maximum
The dioxides and monoxides of elements $X$ and $Y$ are amphoteric in nature. $X$ and $Y$ are respectively
$$ \text { Identify ' } Z \text { ' in the following reaction sequence } $$

What is the major product ' $C$ ' in the following sequence of reactions?

$$ \text { The IUPAC name of the following compound is } $$

$$ \text { Consider the following three resonance structures } $$
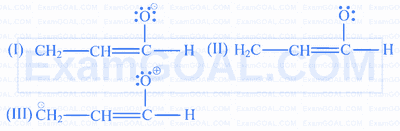
The correct order of their stabilities is
Identify the crystal system in which primitive unit cell has edge lengths $a=b=200 \mathrm{pm}$ and $c=300 \mathrm{pm}$ and all axial angles are same
At 300 K , the osmotic pressure of a decinormal solution of sodium chloride is 4.82 atm . The degree of dissociation of sodium chloride is $x \times 10^{-2}$. The value of $x$ is $\left(R=0.082 \mathrm{~L} \mathrm{~atm} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right)$
At 300 K , the conductivity of $0.01 \mathrm{~mol} \mathrm{dm}^{-3}$ aqueous solution of acetic acid is $19.5 \times 10^{-5} \mathrm{mho} \mathrm{cm}^{-1}$ and limiting molar conductivity of acetic acid at the same temperature is $390 \mathrm{mho} \mathrm{cm}^2 \mathrm{~mol}^{-1}$. The degree of dissociation of acetic acid is
The graph obtained between $\ln k$ ( $k=$ rate constant) on $y$-axis and $1 / T$ on $x$-axis is a straight line. The slope of it is $-4 \times 10^4 \mathrm{~K}$. The activation energy of the reaction (in $\left.\mathrm{kJ} \mathrm{mol}^{-1}\right)$ is $\left(R=831 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right)$
Consider the following about the tyndall effect.
(I) It is used to distinguish between a true and colloidal solution.
(II) It is possible only when the dispersed medium and dispersed phase differ much in their refraction indices.
(III) It is observed only when the size of colloidal particles is much smaller than the wavelength of the light used.
The correct statements are
$$ \text { Match the following. } $$
$$ \begin{array}{llll} \hline & \begin{array}{c} \text { List-I } \\ \text { (Refining method) } \end{array} & & \begin{array}{c} \text { List-II } \\ \text { (Metals to be refined) } \end{array} \\ \hline \text { (A) } & \text { Zone refining } & \text { (I) } & \text { Titanium } \\ \hline \text { (B) } & \text { Poling } & \text { (II) } & \text { Tin } \\ \hline \text { (C) } & \text { Liquation } & \text { (III) } & \text { Gallium } \\ \hline \text { (D) } & \text { Vapour phase refining } & \text { (IV) } & \text { Copper } \\ \hline \end{array} $$
The correct answer is
Assertion (A) : In group 15 elements nitrogen does not form pentahalides.
Reason (R) : Nitrogen can exhibit +5 oxidation state.
The correct option among the following is
In which of the following options, molecules are correctly arranged with respect to their bond angles.
Which of the following reaction represents Deacon's method?
The number of lone pair of electrons present in the valence shell of xenon $(\mathrm{Z}=54)$ in $\mathrm{XeOF}_4, \mathrm{XeF}_4, \mathrm{XeF}_2$ and $\mathrm{XeF}_6$ are respectively
The order of melting points of $\mathrm{Cr}, \mathrm{Mo}$ and W is
Identify the incorrect match from the following.
$$ \text { Match the following } $$
| List-I (Polymer) |
List-II (Monomers) |
||
|---|---|---|---|
| (A) | Bakelite |
(I) | $$ \text { 2-methvl-1, 3-butadiene } $$ |
| (B) | Natural rubber | (II) | $$ \text { Glvcine + aminocaproic acid } $$ |
| (C) | Glyptal | (III) | $$ \text { Phenol + formaldehyde } $$ |
| (D) | Nylon 2-nylon 6 | (IV) | $$ \text { Phthalic acid + ethylene glycol } $$ |
The functional group present in asparagine, a non-essential amino acid, are
The medicine used in controlling depression and hypertension is
Which of the following reaction represents swarts reaction?
Which of the following compound has no reaction with sodium metal?
Which of the following represents Gatterman-Koch reaction?
The major products of Reimer-Tiemann reaction and Kolbe's reaction are respectively
 In the reaction sequence, conversion of $B$ to $C$ is known as
In the reaction sequence, conversion of $B$ to $C$ is known as
What is the major product ' $R$ ' in the following reaction sequence?

$$ \text { Identify what is } Y \text { in the following reaction sequence? } $$

Mathematics
If $f: R \rightarrow R$ is defined by $f(x)=2 x+\sin x, x \in R$, then $f$ is
$$ \left|\begin{array}{ccc} \sqrt{3} & 2 \sqrt{5} & \sqrt{5} \\ \sqrt{15} & 5 & \sqrt{10} \\ 3 & \sqrt{15} & 5 \end{array}\right|= $$
If $A$ is a non-singular matrix such that $(A-2 I)$ $(A-3 I)=0$, then $\frac{1}{5} A+\frac{6}{5} A^{-1}=$
Let $A$ be a matrix such that $A B$ is a scalar matrix, where $B=\left[\begin{array}{ll}1 & 2 \\ 0 & 3\end{array}\right]$ and $\operatorname{det}(3 A)=27$. Then, $3 A^{-1}+A^2=$
If $A$ is a symmetric matrix with real entries, then
$\operatorname{Arg}\left(\sin \frac{6 \pi}{5}+i\left(1+\cos \frac{6 \pi}{5}\right)\right)=$
$$ \text { If } x+i y=\sqrt{\frac{3+i}{1+3 i}}, \text { then }\left(x^2+y^2\right)^2= $$
If the imaginary part of $\frac{2 z+1}{i z+1}$ is -2, then the locus of the point representing $z$ in the Argand plane is
$$ \begin{aligned} &\text { If } \omega \neq 1 \text { is a cube root of unity, then }\\ &\left|\begin{array}{ccc} \omega+\omega^2 & \omega^2+\omega^9 & \omega^9+\omega \\ \omega^{27}+\omega^{31} & \omega^{31}+\omega^{17} & \omega^{17}+\omega^{27} \\ \omega^{30}+\omega^{41} & \omega^{41}+\omega^{19} & \omega^{19}+\omega^{30} \end{array}\right|= \end{aligned} $$
If $i=\sqrt{-1}$, then $(1+i)^{10}+(1-i)^{10}=$
The set of all values of $x$ which satisfy both the inequations $x^2-1 \leq 0$ and $x^2-x-2 \geq 0$ simultaneously is
For all real values of $x$, the minimum value of $\frac{1-x+\lambda^2}{1+x+x^2}$ is
If $\alpha$ and $\beta$ are the roots of the equation $x^2+2 x+2=0$, then $\alpha^{15}+\beta^{15}=$
If the equation whose roots are $P$ times the roots of the equation $x^4-2 a x^3+4 b x^2+8 a x+16=0$ is a reciprocal equation, then $|P|=$
All the letters of the word 'MOTHER' are written in all possible ways and the strings of letters (with or without meaning), so formed are written as in a dictionary order. Then, the position of the word 'THROEM' is
A student is allowed to select at most $n$ books from a collection of ( $2 n+1$ ) books. If the total number of ways in which he can select at least one book is 255 , then the value of $n$ is
The number of integral terms in the expansion of $(\sqrt{3}+\sqrt[8]{5})^{256}$ is
The expansion of $\left(1+x+x^2\right)^{-3 / 2}$ in powers of $x$ is valid, if
If $(1+x)^n=c_0+c_1 x+c_2 x^2+\ldots \ldots+c_n x^n$ for $n \in N$, then $c_0+\frac{c_1}{2}+\frac{c_2}{3}+\ldots \ldots+\frac{c_n}{n+1}=$
If $\frac{x+1}{\left(x^2+1\right)(x-1)^2}=\frac{A x+B}{x^2+1}+\frac{C}{x-1}+\frac{D}{(x-1)^2}$, then $A+B+C+D=$
$$ \text { If } \frac{2 \sin \theta}{1+\cos \theta+\sin \theta}=y, \text { then } \frac{1-\cos \theta+\sin \theta}{1+\sin \theta}= $$
If $\cos \frac{\pi}{7} \cos \frac{2 \pi}{7} \cos \frac{4 \pi}{7}=\frac{\sin \frac{8 \pi}{7}}{8 \sin \frac{\pi}{7}}$, then $\sin \frac{\pi}{14} \sin \frac{3 \pi}{14} \sin \frac{5 \pi}{14} \sin \frac{7 \pi}{14} \sin \frac{9 \pi}{14} \sin \frac{11 \pi}{14} \sin \frac{13 \pi}{14}=$
If $f(\theta)=\cos ^3 \theta+\cos ^3\left(\frac{2 \pi}{3}+\theta\right)+\cos ^3\left(\theta-\frac{2 \pi}{3}\right)$, then $f\left(\frac{\pi}{5}\right)=$
$$ \sinh (\log (3+\sqrt{8}))= $$
In $\triangle A B C$, if $\frac{\cos A}{a}=\frac{\cos B}{b}=\frac{\cos \cdot C}{c}$ and side $a=2$, then area of the $\triangle A B C$ (in sq units) is
If two vectors $\mathbf{a}$ and $\mathbf{b}$ which are perpendicular to each other are such that $|\mathbf{a}|=8$ and $|\mathbf{b}|=3$, then $|\mathbf{a}-2 b|=$
Let $\mathbf{a}$ and $\mathbf{b}$ be non-collinear vectors. If the vectors $(\lambda-1) \mathbf{a}+2 \mathbf{b}$ and $3 \mathbf{a}+\lambda \mathbf{b}$ are collinear, then the set of all possible values of $\lambda$ is
If $M$ is the foot of the perpendicular drawn from $P($ -1,2,-1 ) to the plane passing through the point $A(3,-2,1)$ and perpendicular to the vector $4 \hat{\mathbf{i}}+7 \hat{\mathbf{j}}-4 \hat{\mathbf{k}}$, then the length of $P M$ is
Vectors $\mathbf{p}=a \hat{\mathbf{i}}+b \hat{\mathbf{j}}+c \hat{\mathbf{k}}, \mathbf{q}=d \hat{\mathbf{i}}+3 \hat{\mathbf{j}}+4 \hat{\mathbf{k}}$ and $\mathbf{r}=3 \hat{\mathbf{i}}+\hat{\mathbf{j}}-2 \hat{\mathbf{k}}$ forming a $\triangle A B C$ are such that $\mathbf{p}=\mathbf{q}+\mathbf{r}$. If the area of $\triangle A B C$ is $5 \sqrt{6}$ sq. units, then the sum of the absolute values of $a, b, c$ is
$\mathbf{b}$ and $\mathbf{c}$ are non-collinear vectors and $(\mathbf{c} \cdot \mathbf{c}) \mathbf{a}=\mathbf{c}$. If $(\mathbf{a} \cdot \mathbf{c}) \mathbf{b}-(\mathbf{a} \cdot \mathbf{b}) \mathbf{c}+(\mathbf{a} \cdot \mathbf{b}) \mathbf{b}$ $=(4-2 \beta-\sin \alpha) \mathbf{b}+\left(\beta^2-1\right) \mathbf{c}$, then $\sin (\alpha+\beta)=$
Assertion (A) The variance of the first $n$ odd natural numbers is $\frac{n^2-1}{3}$.
Reason (R) The sum of the first $n$ odd natural numbers is $n^2$ and the sum of the squares of the first $n$ odd natural numbers is $\frac{n\left(4 n^2-1\right)}{3}$.
Which of the following alternatives is correct?
If $A$ and $B$ are two events of a random experiment such that $P(A \cup B)=P(A \cap B)$, then which one amongst the following four options is not true?
If a group of six students including two particular students $A$ and $B$ stand in a row, then the probability of getting an arrangement in which $A$ and $B$ are separated by exactly one student in between them is
$A, B, C, D$ cut a pack of 52 well shuffled playing cards successively in the same order. If the person who cuts a spade first, wins the game and the game continues until this happens, then the probability that $A$ wins the game is
Two bad eggs are mixed accidentally with 10 good ones. If three eggs are drawn at random from this lot in succession without replacement, then the variance of the probability distribution of the number of bad eggs drawn is
The locus of the mid-points of the intercepted portion of the tangents by the coordinate axes, which are drawn to the ellipse $x^2+2 y^2=2$ is
A line $L$ has intercepts $a$ and $b$ on the coordinate axes. When the coordinate axes are rotated through an angle $\alpha$ and keeping the origin fixed, the same line $L$ has intercepts $p$ and $q$ on the new axes. Then,
Two lines $L_1$ and $L_2$ passing through the point $P(1,2)$ cut the line $x+y=4$ at a distance of $\frac{\sqrt{6}}{3}$ units from $P$. Then, the angles made by $L_1, L_2$ with positive $X$-axis are
A pair of straight lines drawn though the origin forms. an isosceles triangle right angled at the origin with the line $2 x+3 y=6$. The area (in sq units) of the triangle, so formed is
The equation of the straight line passing through the point $(3,2)$ and inclined at an angle of $60^{\circ}$ with the line $\sqrt{3} x+y=1$ is
An equilateral triangle is constructed between the lines $\sqrt{3} x+y-6=0$ and $\sqrt{3} x+y+9=0$ with base on one line and vertex on the other. The area (in sq units) of the triangle, so formed is
If $\theta$ is the acute angle between the lines joining the origin to the points of intersection of the curve $x^2+x y+y^2+x+3 y+1=0$ and the straight line $x+y+2=0$, then $\cos \theta=$
If a circle passing through $(1,-2)$ has $x-y=2$ and $2 x+3 y=14$ as its diameters, then the radius of the circle is
The equation of the circle whose diameter is the common chord of the circles $x^2+y^2+2 x+3 y+1=0$ and $x^2+y^2+4 x+3 y+2=0$ is
The pole of the straight line $9 x+y-28=0$ with respect to the circle $2 x^2+2 y^2-3 x+5 y-7=0$ is
The equation of the line perpendicular to the radical axis of two circles $x^2+y^2-5 x+6 y+12=0$, $x^2+y^2+6 x-4 y-14=0$ and passing through $(1,1)$ is
If the angle between the circles
$$ x^2+y^2-2 x-4 y+c=0 \text { and } x^2+y^2-4 x-2 y+4=0 $$
is $60^{\circ}$, then $c=$
The normal at a point on the parabola $y^2=4 x$ passes through $(5,0)$. If there are two more normals to this parabola passing through $(5,0)$, then the equation of one of these normals is
The equations of common tangents to the parabola $y^2=16 x$ and the circle $x^2+y^2=8$ are
The product of the lengths of the perpendiculars drawn from the two foci of the ellipse $\frac{x^2}{9}+\frac{y^2}{25}=1$ to the tangent at any point on the ellipse is
Tangents are drawn to the ellipse $\frac{x^2}{9}+\frac{y^2}{5}=1$ at all the ends of its latus recta. The area of the quadrilateral, so formed (in sq units) is
$P(a \sec \theta, b \tan \theta)$ and $Q(a \sec \phi, b \tan \phi)$ are two points on the hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ where, $\phi+\theta=\frac{\pi}{2}$. If $(h, k)$ is the point of intersection of the normals drawn at $P$ and $Q$, then $k=$
If $A=(1,-1,2), B=(3,4,-2), C=(0,3,2)$ and $D=(3$, $5,6)$, then the angle between the lines $\mathbf{A B}$ and $\mathbf{C D}$ is
Consider the following statements:
Assertion (A) : The direction ratios of a line $L_1$ are 2,5, 7 and the direction ratios of another line $L_2$ are $\frac{4}{\sqrt{19}}$, $\frac{10}{\sqrt{19}}, \frac{14}{\sqrt{19}}$. Then, the lines $L_1, L_2$ are parallel.
Reason : ( $\mathbf{R}$ ) If the direction ratios of a line $L_1$ are $a_1, b_1, c_1$ the direction ratios of a line $L_2$ are $a_2, b_2, c_2$ and $a_1 a_2+b_1 b_2+c_1 c_2=0$, then the lines of $L_1, L_2$ are parallel.
A line $L$ is parallel to both the planes $2 x+3 y+z=1$ and $x+3 y+2 z=2$. If line $L$ makes an angle $\alpha$ with the positive direction of $X$-axis, then $\cos \alpha=$
$$ \lim\limits_{x \rightarrow 1}(1-x) \tan \left(\frac{\pi}{2} x\right)= $$
If $f(9)=9$ and $f^{\prime}(9)=4$, then $\lim\limits_{x \rightarrow 9} \frac{\sqrt{f(x)}-3}{\sqrt{x}-3}=$
If $\sec \left(\log _2 y^2\right)=\operatorname{cosec}\left(\log _2 x^2\right)$, then $\frac{d y}{d x}=$
If $e^x=y+\sqrt{y^2-1}$, then $\frac{d y}{d x}=$
If $x=\log p$ and $y=\frac{1}{p}$, then $\frac{d y}{d x}=$
Electric current $(I)$ is measured by galvanometer, the current being proportional to the tangent of the angle ( $\theta$ ) of deflection. If the deflection is read as $45^{\circ}$ and an error of $1 \%$ is made in reading it, the percentage error in the current is
If the equation of a tangent drawn to the curve $y=\cos (x+y),-1 \leq x \leq 1+\pi$ is $x+2 y=k$, then $k=$
$f: R \rightarrow R$ is a function defined by $f(x)=\frac{1}{e^x+2 e^{-x}}$
Assertion (A) : $f(c)=\frac{1}{3}$ for some values of $c \in R$
Reason (R) : $0 < f(x) \leq \frac{1}{2 \sqrt{2}}$ for all $x \in R$
Then, which of the following options is correct?
| List-I | List-II |
| 1. |
A. |
| 2. |
B. |
| 3. |
C. |
| 4. |
D. |
| E. |
$$ \int_0^{\pi / 4} \frac{\sec x}{1+2 \sin ^2 x} d x= $$
If $\int x^4(\log x)^3 d x=x^5\left[A(\log x)^3\right]$ $\left.+B(\log x)^2+C \log x+D\right]+k$, then $A+B+C+5 D=$
$$ \lim\limits_{n \rightarrow \infty}\left[\frac{1}{n^2} \sec ^2 \frac{1}{n^2}+\frac{2}{n^2} \sec ^2 \frac{4}{n^2}+\ldots \ldots+\frac{1}{n} \sec ^2 1\right]= $$
$$ \int\limits_2^5 \sqrt{\frac{5-x}{x-2}} d x= $$
$$ \int\limits_0^{\frac{\pi}{2}} \sin ^6 x \cos ^4 x d x= $$
The area (in sq units) bounded by the curve $y=2 x-x^2$ and the line $y=-x$ is
The degree and order of the differential equation of the family of parabolas whose axis is the $X$-axis, are respectively
The general solution of the differential equation $\left(x \sin \frac{y}{x}\right) d y=\left(y \sin \frac{y}{x}-x\right) d x$ is
Physics
If $F_1$ and $F_2$ are the relative strengths of the gravitational and weak nuclear forces respectively, then $F_2 / F_1$ is nearly
The number of significant figures in $3.78 \times 10^{22} \mathrm{~kg}$ is
The ratio of the displacements of a freely falling body during first, second and third seconds of its motion is
A person walks in such a way that he covers equal distance in each step. The person takes 2 steps forwards towards east, then takes a right turn and
walks 4 steps towards south, then takes a right turn and walks 6 steps towards west and then takes a right turn and walks further. The direction of his final position after a total of 20 steps walk with respect to his initial position is
While a person climbs stairs, the gravitational potential energy of the person increases. The source of this energy is
Moon revolves around the earth in an orbit of radius $R$ with time period of revolution $T$. It also rotates about its own axis with a time period $T$. If mass of the moon is $M$ and its radius is $r$, the total kinetic energy of the moon is
The spinning of the Diwali cracker 'ground chakkar' involves the concept of
A clock is designed based on the oscillation of a spring-block system suspended vertically in the absence of air-resistance. Assume it shows the correct time when a spring of stiffness $k$ and block is mass $m$ are used. If the block is replaced by another block of mass $4 m$, choose the correct option
A body of mass 6 kg is moving with a uniform velocity $4 \mathrm{~ms}^{-1}$. Its velocity changes to $6 \mathrm{~ms}^{-1}$ when a force of 12 N acts on it. Then its displacement is
Two wires $A$ and $B$ of same length, same radius and same Young's modulus are heated to same range of temperatures. If the coefficient of linear expansion of $A$ is $\frac{3}{2}$ times that of $B$, then the ratio of the thermal stresses produced in the two wires $A$ and $B$ is
If the work done in blowing a soap bubble of radius $R$ is $W$, then the work done in blowing the soap bubble of radius $2 R$ is
Three identical vessels are filled with three liquids ${ }_{A, B}$ and $C$ with equal masses but having densities $\rho_{A, \rho_B}$ and $\rho_C$ respectively. If $\rho_A>\rho_B>\rho_C$ then the pressure at the bottom of the vessels will be
Two rod of same area of cross-section have lengths $L$ and $2 L$ and coefficients of linear expansions $2 \alpha$ and $a$ respectively. If they are welded to form a composite rod of length $3 L$ then the coefficient of linear expansion of the composite rod is
For a given mass of a gas at constant temperature, the volume and the pressure are $V$ and $p$ respectively. Then the slope of the graph drawn between $\log _e V$ on $X$-axis and $\log _e p$ on $Y$-axis is
An ideal gas at $127^{\circ} \mathrm{C}$ is compressed suddenly to $8 / 27 \mathrm{}$of its initial volume. If $\gamma=5 / 3$ for an ideal gas, then rise in its temperature is
An insulating cylinder contains 4 moles of an ideal diatomic gas. When a heat $Q$ is supplied to it, 2 moles of the gas molecules dissociate. If the temperature of the gas remains constant, then the value of $Q$ is ( $R=$ universal gas constant)
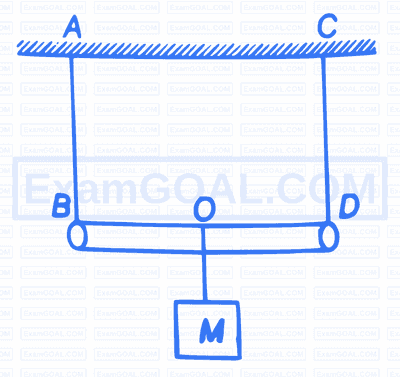
A rod of length $L$ and negligible mass is suspended by two identical strings $A B$ and $C D$ as shown in the figure A mass $M$ is suspended from point $O$ which is at a distance $x$ from $B$. If the frequency of the first harmonic of $A B$ is equal to the frequency of the second harmonic of $C D$, then the value of $x$ is
An observer moves towards a stationary source of sound with a speed $\frac{1}{5}$ th that of sound. The frequency of ${ }^{\text {th }}$ sound emitted by the source of $f$. The apparent frequency recorded by the observer is
The angles of incidence and emergence of a light ray passing through a prism of angle $A$ are $i$ and $e$ respectively. The total deviation produced by the prism is
If the slit width is 2 mm and wavelength of light used is $4000\mathop {\rm{A}}\limits^{\rm{o}}$, then Fresnel distance is nearly
If a capacitor of capacitance $100 \mu \mathrm{~F}$ is charged at a steady rate of $100 \mu \mathrm{C} \mathrm{s}^{-1}$, then the time taken to produce a potential difference of 100 V between the capacitor plates is
A potentiometer balances at 44 cm when a cell of internal resistance $1 \Omega$ is in the secondary circuit. To obtains the balancing point at 40 cm , the resistance to be connected parallel to cell is
Two wires made of the same material have lengths in the ratio $2: 3$ and radii in the ratio $8: 9$. If the same potential difference is applied across the ends of the wires, the ratio of the electric currents flowing through them is
The magnetic field at a perpendicular distance of one metre from a wire carrying current of 1 A is
A circular coil of area $2 \mathrm{~cm}^2$ has 1000 turns. If the current through the coil is 1 A , then its magnetic moment is
The magnetic susceptibility of ferromagnetic materials is
If the vertical component of earth's magnetic field is $0.5 \times 10^{-4} \mathrm{~T}$ at a point. When an aeroplane of wing span 4 m is moving horizontally at this place at $360 \mathrm{kmh}^{-1}$, then the motional emf forced across the ends of the wings is
A boy is playing with the empty rim of a cycle wheel of radius 40 cm by rolling it along a horizontal road towards north with angular speed of $20 \mathrm{rad} \mathrm{s}^{-1}$. Considering the effect of magnetic field of earth, the e.m.f induced in the rim is
(Horizontal component of earth's magnetic field $=0.26 \mathrm{G}$ )
In an ideal step up transformer, if the input voltage and input power are $V_1$ and $R_1$ respectively and the output voltage and output power are $V_2$ and $P_2$ respectively, then
The correct statement among the following is
The additional energy that should be given to an electron to reduce its de-Broglie wavelength from 1 nm to 0.5 nm is
In the following nuclear reaction $X$ is
$$ { }_{13} \mathrm{Al}^{27}+{ }_2 \mathrm{He}^4 \longrightarrow{ }_0 n^1+X $$
When a semiconductor is doped with donor impurity
The need for modulation is