All the springs in fig. (a), (b) and (c) are identical, each having force constant K each. Mass m is attached to each system. If $\mathrm{T}_a, \mathrm{~T}_b$ and $\mathrm{T}_{\mathrm{c}}$ are the time periods of oscillations of the three systems in fig. (a), (b) and (c) respectively, then

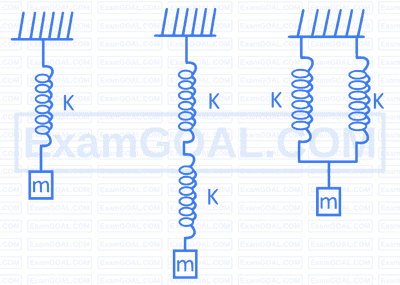
A physical quantity ' X ' is related to four measurable quantities ' $a$ ', ' $b$ ', ' $c$ ' and ' $d$ ' as $\mathrm{X}=\mathrm{a}^2 \mathrm{~b}^3 \mathrm{c}^{5 / 2} \mathrm{~d}^{-2}$. The percentage error in the measurement of 'a', 'b', 'c' and 'd' are $1 \%$, $2 \%, 2 \%$ and $4 \%$ respectively. The percentage error in measurement of quantity ' X ' is

A coil of effective area $3 \mathrm{~m}^2$ is placed at right angles to a magnetic field of induction $0.05 \mathrm{~Wb} / \mathrm{m}^2$ If the field is decreased to $20 \%$ of its original value in 10 second, the e.m.f. induced in the coil will be

Two vectors $a \hat{i}+b \hat{j}+\hat{k}$ and $2 \hat{i}-3 \hat{j}+4 \hat{k}$ are perpendicular to each other. When $3 \mathrm{a}+2 \mathrm{~b}=7$, the ratio of $a$ to $b$ is $\frac{x}{2}$. The value of $x$ is