500 gram of a diatomic gas is enclosed at a pressure of $10^5 \mathrm{Nm}^{-2}$. The density of the gas is $5 \mathrm{kgm}^{-3}$. The energy of one mole of the gas due to its thermal motion is [consider the gas molecule as a rigid rotator]

In metre-bridge experiment the balance point is obtained if the gaps are closed by $2 \Omega$ and $3 \Omega$. A shunt of $\mathrm{x} \Omega$ is added to $3 \Omega$ resistor to shift the balance point by 22.5 cm . The value of x is

All the springs in fig. (a), (b) and (c) are identical, each having force constant K each. Mass m is attached to each system. If $\mathrm{T}_a, \mathrm{~T}_b$ and $\mathrm{T}_{\mathrm{c}}$ are the time periods of oscillations of the three systems in fig. (a), (b) and (c) respectively, then

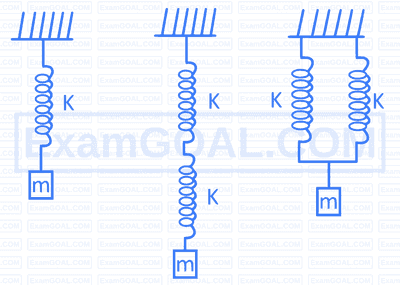
A physical quantity ' X ' is related to four measurable quantities ' $a$ ', ' $b$ ', ' $c$ ' and ' $d$ ' as $\mathrm{X}=\mathrm{a}^2 \mathrm{~b}^3 \mathrm{c}^{5 / 2} \mathrm{~d}^{-2}$. The percentage error in the measurement of 'a', 'b', 'c' and 'd' are $1 \%$, $2 \%, 2 \%$ and $4 \%$ respectively. The percentage error in measurement of quantity ' X ' is