Chemistry
1. What volume of $0.2 \mathrm{M} \mathrm{CH}_3 \mathrm{COOH}$ needs to be added to 100 ml of $0.4 \mathrm{M} \mathrm{CH}_3 2. Identify the final product $[Z]$ formed when Chlorobenzene undergoes the given series of reactions:
3. Two volatile liquids X and Y form an ideal solution at 298 K and have vapour pressures equal to 100 mm and 200 mm of Hg 4. 0.4 g of Propane burns completely at 300 K in a bomb calorimeter. The temperature of the calorimeter and surrounding wat 5. Match the metals in Column II with their characteristic properties given in Column I.
.tg {border-collapse:collapse;bo 6. Convert Benzene $\rightarrow 3$-Bromophenol by choosing appropriate reagents [(i) to (v)] in the correct sequence.
(i) $ 7. Choose the correct statement. 8. An aqueous solution of $\mathrm{CrCl}_3 .6 \mathrm{H}_2 \mathrm{O}$ (Molar mass $=266.5 \mathrm{~g} / \mathrm{mol}$ ) co 9. In which one of the following pairs does the stability of the monovalent ion increase with respect to the molecule, whil 10. When $9.2 \times 10^{-3} \mathrm{~kg}$ of formic acid is added to 600 ml of water the freezing point of water is depress 11. An organic compound $[\mathrm{X}]$ (molecular formula- $\mathrm{C}_5 \mathrm{H}_{11} \mathrm{NO}$ when reacted with $\ma 12. Choose the correct statement. 13. Two statements, One Assertion (A) and the other Reason (R) are given. Choose the right option.
Assertion: The rate const 14. Which one of the following is a true statement with reference to reaction between 2- Bromo-2-methylpropane and aqueous K 15. Which of the following haloalkanes will give more than one isomeric product, on being heated with alc. KOH ? 16. Which one of the following coordination compounds will exhibit both geometrical and optical isomerism? 17. The concentration and percentage purity of Oxalic acid can be determined by titration with $\mathrm{KMnO}_4$ in presence 18. What is the final product $[\mathrm{Z}]$ formed when the given reactions take place?
19. A non-volatile solute A weighing 60 g when dissolved in 212 g of the solvent Xylene reduces its vapour pressure to $60 \ 20. Two statements, one Assertion (A) and the other Reason (R) are given. Choose the correct option.
Assertion: Compound $[\ 21. For a 1.0 molal solution containing the non-volatile solute Urea, the elevation in boiling point is 2.0 K while the depr 22. Identify the correct statement. 23. Choose the incorrect statement. 24. Solubility product of the sparingly soluble salt $\mathrm{AgBrO}_3$ in aqueous medium is $9.3 \times 10^{-10}$ Calculate 25. What is the reduction potential of a half-cell consisting of a Pt electrode dipped in $2.2 \mathrm{M} \mathrm{Fe}^{2+}$ 26. Both reactions (i) and (ii) give the same compound X as the major product. Identify X
(i). 3-Methylbut-1-ene $+\mathrm{H 27. Two chemical reactions of the same order have equal Frequency factor value. Their Activation energies differ by $26.8 \m 28. Arrange the following compounds in the decreasing order of the molar conductivities of their aqueous solutions.
.tg {b 29. From the given covalent compounds (A to F) identify the pair of molecules which have:
(i) Two lone pairs of electrons on 30. A current of 2.5 amperes is passed through 800 ml of 0.48 M solution of $\mathrm{CuSO}_4$ for 1.0 hour with a current ef 31. A certain orbital having 2 angular nodes and no radial nodes is: 32. An organic compound $[\mathrm{X}]$ reacts with $\mathrm{H}_2 / \mathrm{Pd}-\mathrm{BaSO}_4$ to give compound $[\mathrm{Y 33. Arrange the following free radicals in the increasing order of their stability:
.tg {border-collapse:collapse;border-s 34. If X is a haloalkane with a single Chlorine atom per molecule and the percentage of Cl is 55 , what would be the number 35. For a reaction $\mathrm{X}_2(\mathrm{l})+\mathrm{Y}_2(\mathrm{~g}) \leftrightharpoons 2 \mathrm{XY}(\mathrm{g})$, the $\ 36. Which one of the following reactions does not give the correct combination of reactants and the major products formed in 37. Match the coordination compounds in Column I having the given type of hybridisation of $\mathrm{M}^{\mathrm{n}+}$ ion an 38. The EMF of the cell $\mathrm{Al} / \mathrm{Al}^{3+}(0.01 \mathrm{M}) \| \mathrm{Fe}^{2+}(0.02 \mathrm{M}) / \mathrm{Fe}$ 39. An unsaturated hydrocarbon $[\mathrm{A}]$ undergoes the following series of reactions. Identify $[\mathrm{A}]$.
40. Identify the compound which gives an optically active haloalkane on reaction with $\mathrm{H}_2$ / Ni on heating.
.tg 41. For a given reaction of the type $\frac{3}{5} X(a q) \rightarrow \frac{1}{2} Y(a q)+Z(g)$, the correct expression for th 42. Which one of the following statements is correct?. 43. Given that the standard enthalpy of combustion of $\mathrm{C}_{(\mathrm{S})}$ and $\mathrm{CS}_2(\mathrm{l})$ are -393.3 44. Choose the correct statement. 45. Benzene diazonium chloride when warmed with water gives a compound, whose Sodium salt when reacted with Allyl bromide gi 46. Arrange the following in the decreasing order of their $\mathrm{pK}_{\mathrm{a}}$ values.
47. Cyclohexanol undergoes a series of reactions as given. Identify compound (iv).
$\mathrm{C}_6 \mathrm{H}_{11} \mathrm{OH} 48. Match the structures in Column I with their correct IUPAC names given in Column II.
.tg {border-collapse:collapse;bord 49. Identify $[\mathrm{X}]$, the final product formed when 2 moles of Ethanal undergoes the following series of reactions wi 50. Two statements, one Assertion (A) and the other Reason (R) are given. Choose the correct option.
Assertion: Maltose, a d 51. Which one of the following options represents the decreasing order of oxidation number of the central atom in:
$$\mathrm 52.
What is the spin only magnetic moment of the metal ion in $\mathbf{P}$ and the oxidation number of Sulphur in the oxidi 53. The conductivity of 0.01 M solution of $\mathrm{CH}_3 \mathrm{COOH}$ at 298 K is $1.65 \times 10^{-4} \mathrm{Scm}^{-1}$ 54. Two statements, one Assertion (A) and the other Reason (R) are given. Choose the correct option.
Assertion: 2-aminoethan 55. $\mathrm{X} \rightarrow 2 \mathrm{Y}$ is a first order reaction where $1.0 \mathrm{~mol} / \mathrm{L}$ of the reactant y 56. Match the reactions of Glucose given in Column I with the major product formed in the reaction as in Column II.
.tg {b 57. A certain gas absorbs photon of wavelength $4.0 \times 10^{-7} \mathrm{~m}$ and emits radiation at two wavelengths. If o 58. The following results were obtained during study of the reaction $2 \mathrm{NO}(\mathrm{g})+\mathrm{Cl}_2(\mathrm{~g}) \ 59. Two statements, One Assertion [ A ] and the other Reason [ R ] are given. Identify the correct option
Assertion $[A]$ :
Mathematics
1. The solution of $(x+\log y) d y+y d x=0$ when $y(0)=1$ is 2. The order of the differential equation $\frac{d}{d x}\left[\left(\frac{d y}{d x}\right)^3\right]=0$ is 3. Find the value of $\lim\limits_{h \rightarrow 0} \frac{(a+h)^2 \sin (a+h)-a^2 \sin a}{h}$ 4. $0.2+0.22+0.022+\ldots \ldots \ldots$. up to $n$ terms is equal to 5. The solution set of the system of inequalities $5-4 x \leq-7$ or $5-4 x \geq 7, x \in R$ is 6. $-\frac{2 \pi}{5}$ is the principal value of 7. The digits of a three-digit number taken in an order are in geometric progression. If one is added to the middle digit, 8. The least value of ' $a$ ' such that the function $x^2+a x+1$ is increasing on $[1,2]$ is 9. Three fair dice are thrown. What is the probability of getting a total of 15 given that they exhibit three different num 10. The variance of 25 observations is 8 . If each observation is multiplied by 3 , then the new variance of the resulting o 11. P is a point on the line joining the points $(3,5,-1)$ and $(6,3,-2)$. If $y$ coordinate of point P is 2 , then $x$ coor 12. If $\vec{a}, \vec{b}, \vec{c}$ are three vectors such that $a \neq 0$ and $\vec{a} \times \vec{b}=2(\vec{a} \times \vec{ 13. The general solution of the differential equation $(x-y) d y=(x+y) d x$ is 14. A line $L_1$ passes through the points $(h, k),(1,2)$ and $(-3,4)$. The points $(4,3)$ and $(h, k)$ lie on the line $L_2 15. Let $M$ be the set of all $2 \times 2$ matrices with entries from the set R of real numbers. Then the function $f: M \ri 16. The sum of three numbers is 6 .
Twice the third number, when added to the first number gives 7 ,
On adding the sum of th 17. $\int \frac{1}{\sqrt{9+8 x-x^2}} d x=\varphi(x)+c$ then $\varphi(x)=$ 18. A person writes four letters and address four envelopes. If the letters are placed in the envelopes at random, then the 19. $\int \tan ^2\left(5-\frac{x}{2}\right) d x=$ 20. If $f(x)=\left(\frac{3+x}{1+x}\right)^{2+3 x}$, then $f^{\prime}(0)=$ 21. If $A(t)=\left[\begin{array}{cc}\cos t & \sin t \\ -\sin t & \cos t\end{array}\right]$ then the product of $A(t)$ and $A 22. If $A=\left[\begin{array}{cc}1 & -2 \\ 4 & 5\end{array}\right] ; f(t)=t^2-3 t+7$ then $f(A)+\left[\begin{array}{cc}3 & 6 23. Codes used for vehicle identification consists of two distinct English alphabets followed by two distinct digits from 1 24. Equation of a circle whose area is 154 sq units and having $2 x-3 y+12=0$ and $x+4 y-5=0$ as diameters is 25. If $y=\sqrt{\frac{x}{a}}+\sqrt{\frac{a}{x}}, \quad$ then $2 x y \frac{d y}{d x}$ is equal to 26. Let $A$ and $B$ be two events such that one of the two events must occur. Given that the chance of occurrence of $A$ is 27. For two matrices $A$ and $B$, given that $A^{-1}=\frac{1}{8} B$ then inverse of $(8 A)$ is 28. Distance of the point $(-2,3)$ from the line $12 x-5 y-2=0$ is $\frac{41}{k}$. Then the value of $k$ is 29. If $\sin A+\sin B=-\frac{21}{65}, \cos A+\cos B=-\frac{27}{65}$ and $\pi 30. If $A=\left[\begin{array}{ccc}0 & 1 & -2 \\ -1 & 0 & 3 \\ 2 & -3 & 0\end{array}\right]$ then $A^{-1}$ 31. Area of the region bounded by the curve $y=\sin \left(\frac{x}{2}\right)$ between $-4 \pi$ and 0 is 32. $\int \log x^2 d x=$ 33. The value of $\lambda$ for which the angle between lines $\vec{r}=\hat{\imath}+\hat{\jmath}+\hat{k}+p(2 \hat{\imath}+\ha 34. The value of $\frac{1}{2 \sin 10^{\circ}}-2 \sin 70^{\circ}$ is 35. If two vertices of a triangle are $(3,-2)$ and $(-2,3)$ and its orthocentre is $(-6,1)$.
Then the difference between ord 36. The area bounded by the parabola $y^2=36 x$ and its latus rectum is 37. If $n(A)=3$ and $n(B)=7$ and $A \subseteq B$ then the number of elements in $A \cap B$ is equal to 38. If $y=\sin ^{-1}\left(\frac{1}{\sqrt{x+1}}\right)$ then $\frac{d y}{d x}=$ 39. $\int_0^\pi \frac{e^{\cos x}}{e^{\cos x}+e^{-\cos x}} d x$ is equal to 40. The range of $x$ for which the equation $\sin ^{-1}\left(\frac{2 x}{1+x^2}\right)=2 \tan ^{-1} x$ holds true 41. A spherical snowball is melting such that its volume is decreasing at the rate of $1 \mathrm{~cm}^3 / \mathrm{min}$. The 42. For a given Linear Programming problem, the objective function is
$$z=3 x+2 y$$
Subject to constraints are
$$\begin{alig 43. The curve $a x^3+b x^2+c x+d$ has a point of minima at $x=1$, then 44. If $\tan x^{\circ} \tan 2^{\circ} \tan 3^{\circ} \ldots \ldots \ldots \ldots . . \tan 88^{\circ} \tan y^{\circ}=1$ then 45. Vasant and Jothi play a game with a coin. Vasant stakes ₹ 1 and throw the coins four times.
If he throws four heads, he 46. The solution of the differential equation $\frac{d y}{d x}+y \log y \cot x=0$ is 47. A shopkeeper sells three varieties of fruit juice. He has a large number of bottles of same size of each variety. The nu 48. The value of $\lim _\limits{x \rightarrow 0} \frac{(1-x)^n-1}{x}=$ 49. If $f(x)=\left\{\begin{array}{ll}\frac{1-x^m}{1-x} & \text { if } x \neq 1 \\ 2 m-1 & \text { if } x=1\end{array}\right. 50. $\int \frac{d x}{(x+2)\left(x^2+1\right)}=p \log |x+2|+q \log \left|x^2+1\right|+r \tan ^{-1} x+c$ then $p+q+r=$ 51. Let R be a relation on natural numbers defined by $x+2 y=8, x, y \in N$. The domain of R is 52. Oil from a conical funnel is dripping at the rate of $5 \mathrm{~cm}^3 / \mathrm{s}$. If the radius and height of the fu 53. If the third and fourth terms in the expansion $\left(2 x+\frac{1}{8}\right)^{10}$ are equal, then the value of $x$ is _ 54. Identify the correct statement 55. If $\frac{x-1}{3+i}+\frac{y-1}{3-i}=i$ then $(y, x)=$ 56. A line $L_1$ passing through the point A with position vector $\vec{a}=4 \hat{i}+2 \hat{j}+2 \hat{k}$ is parallel to the 57. If the distance between the foci is equal to the length of the latus rectum, then the eccentricity of the ellipse is 58. In an entrance test, there are multiple choice questions. There are four possible answers to each question of which only 59. The magnitude of the projection of the vector $-\hat{\imath}+2 \hat{\jmath}-\hat{k}$ on the z -axis is 60. A solid S is made from a cylinder surmounted by a hemisphere on top with both its circular faces sharing a common centre
Physics
1. According to Bohr's theory of hydrogen atom, the speed of the electron, its energy and radius of its orbit vary with the 2. A particle of mass $M$ at rest decays into masses $m_1$ and $m_2$ with non-zero velocities. The ratio of de Broglie wave 3. The nuclear forces
a. are central forces, independent of the spin of the nucleons.
b. have a short-range dominant over a 4. Two light rays A and B travel from a medium into air at angles of incidence 15 degrees and 42 degrees respectively. In t 5. An electric field $E=3 x^2 i N C^{-1}$ exists in a certain region of space. The potential difference between the origin 6. A current loop consists of two identical semicircular parts each of radius $2 R$, one lying in the $x-y$ plane and the o 7. Which of the following is not a characteristic of diamagnetism? 8. An ideal inductor is connected across a capacitor. Oscillations of energy $K$ are set up in the circuit. The capacitor p 9. A symmetric double convex lens is cut into two equal parts by a plane perpendicular to the principal axis. If the power 10. Three identical conducting balls $\mathrm{A}, \mathrm{B}$ and C , each of mass m , are thrown upward at an angle $\Theta 11. In a single slit Fraunhofer diffraction pattern obtained at normal incidence, at the angular position of the second diff 12. The magnetic flux $\phi$ through a stationary loop of wire having a resistance R varies with time as $\phi=4 t^2+3 t$. T 13. A stone is dropped from a height $h$. It hits the ground with a certain momentum ' $p$ '. If the same stone is dropped f 14. Point charges $-3 Q,-q, 2 q$ and $2 Q$ are placed, one at each corner of a square. The relation between Q and q for whic 15. If $R$ and $L$ denote resistance and inductance of a material, then the dimension of $L R$ will be: 16. A student measures the terminal potential difference $V$ of a cell (emf $\varepsilon$ and internal resistance $r$ ) as a 17. A galvanometer of resistance $50 \Omega$ is connected to a battery of 4 V along with a resistance of $3950 \Omega$ in se 18. Two capacitors $\mathrm{C}_1$ and $\mathrm{C}_2$ are charged to 100 V and 120 V respectively. It is found that upon conn 19. Two very long, straight, parallel wires carry steady currents I and 21 respectively. The distance between the wires is d 20. A bulb of resistance 280 Ohm is supplied with a voltage $\mathrm{V}=400 \sin \pi \mathrm{t}$. The peak current is 21. A wooden block floats with $\frac{3}{5}$ of its volume submerged in a tank of water. If a denser liquid is poured into t 22. A particle starts from rest and moves along the x -axis with a velocity that varies as $\mathrm{v}=\sqrt{100+4 x} \mathr 23. One surface of a lens is convex and the other is concave. If the radii of curvatures are $R$ and $r$ respectively, the l 24. Emission of electrons from a metal plate illuminated with monochromatic electromagnetic radiation will always take place 25. A charged particle is released from rest in a region of space in which steady and uniform electric and magnetic fields a 26. If E is the amplitude of the electric field of the waves starting from the slits in a double slit experiment and $\theta 27. Two coherent waves of intensities $I_1$ and $I_2$ pass through a region at the same time in the same direction. The sum 28. A Si and a Ge diode has identical physical dimensions. The band gap in Si is larger than that in Ge. On applying identic 29. A convex lens forms a real image of an object with magnification $m_1$. The lens is moved towards the object to obtain a 30. For the charge configuration shown here, which of the following is not true?
31. A bomb of mass 20 kg at rest explodes into two pieces of masses 12 kg and 8 kg . If the velocity of 8 kg mass is $6 \mat 32. Two identical conducting balls having positive charges $q_1$ and $q_2$ are separated by a distance $r$. If they are made 33. Two simple harmonic motions are represented by equations $y_1=0.5 \sin \left[200 \pi \mathrm{t}+\frac{\pi}{3}\right]$ an 34. Two identical conductors of lengths 1 and 31 respectively are maintained at the same temperature. They are given potenti 35. If voltage across a bulb rated $220 \mathrm{~V}, 50 \mathrm{~W}$ drops by $5 \%$ of its rated value, the percentage of t 36. A vertical spring of spring constant $24 \mathrm{Nm}^{-1}$ is fixed on a table. A ball of mass 0.5 kg at a height 2 m ab 37. The resistance of a wire is 5 ohm at $25^{\circ} \mathrm{C}$ and 7 ohm at $100^{\circ} \mathrm{C}$. The resistance of th 38. A sonometer string vibrates with a frequency of 400 Hz . When the length of the string is halved and the tension is alte 39. In an experiment to measure the density of the material of a sphere, an error of $2 \%$ occurred while measuring the rad 40. The radius of earth is $R$ and acceleration due to gravity on its surface is $g$. The height at which the acceleration d 41. A block of metal A is connected in series with another block of metal B such that the two metal blocks have the same are 42. The mean energy per molecule for a diatomic gas is: 43. An LCR series ac circuit is at resonance with 10 V each across $\mathrm{L}, \mathrm{C}$ and R . If the resistance is hal 44. Which, of the following is true of the Balmer series of the hydrogen spectrum?
a. The series is in the visible region.
b 45. If the binding energy per nucleon in $3 \mathrm{Li}^7$ and ${ }_2 \mathrm{He}^4$ nuclei are respectively 5.60 MeV and 7. 46. From a circular disc of radius 2 R , a smaller circular disc is cut with radius of the larger disc as its diameter. The 47. The ratio of specific heat capacities at constant pressure to that at constant volume for a given mass of a gas is $\fra 48. A planet is 121 times heavier than moon and has a diameter 9 times that of moon. If the escape velocity on the planet is 49. The electrical conductivity of a semiconductor increases when electromagnetic radiation of wavelength shorter than $1.24 50. In a nuclear fusion reaction, two nuclei, $A$ and $B$ fuse to produce a nucleus $C$, releasing an amount of energy $\Del 51. In the energy band diagram of a material shown below, open circles and filled circles denote holes and electrons respect 52. A particle moves towards west with a velocity of $10 \mathrm{~ms}^{-1}$. After 10s its direction changes towards south a 53. The electric and magnetic fields associated with an electromagnetic wave propagating along +z axis, can be represented b 54. A bar magnet is oscillating in the earth's magnetic field with a period $T$. When the length of the bar magnet is double 55. A cylindrical tank 0.5 m in radius, rests on a platform 1.5 m high. Initially the tank is filled with water to a height 56. A long solenoid has 400 turns. When a current of 100 A is passed through it, the resulting magnetic flux linked with eac 57. Which of the following is not true for a perfect conductor? 58. Young's modulus of the material of wires X and Y are in the ratio 4:1 and the areas of cross sections of the wires X and 59. A force of $-\mathrm{F} \hat{\mathbf{i}}$ acts at the origin of the coordinate system. The torque about the point $(0,1, 60. A sample of an ideal gas is taken through the cyclic process ABCA as shown in figure below. It absorbs 60 J of heat duri
1
COMEDK 2025 Morning Shift
MCQ (Single Correct Answer)
+1
-0
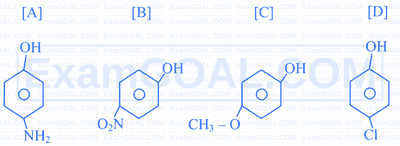
Arrange the following in the decreasing order of their $\mathrm{pK}_{\mathrm{a}}$ values.
A
$\mathrm{A}>\mathrm{C}>\mathrm{D}>\mathrm{B}$
B
$\mathrm{C}>\mathrm{A}>\mathrm{B}>\mathrm{D}$
C
$\mathrm{B}>\mathrm{D}>\mathrm{C}>\mathrm{A}$
D
$\mathrm{D}>\mathrm{C}>\mathrm{A}>\mathrm{B}$
2
COMEDK 2025 Morning Shift
MCQ (Single Correct Answer)
+1
-0
Cyclohexanol undergoes a series of reactions as given. Identify compound (iv).
$\mathrm{C}_6 \mathrm{H}_{11} \mathrm{OH}+\mathrm{CrO}_3 \rightarrow(\mathrm{i})+\mathrm{C}_6 \mathrm{H}_5 \mathrm{MgI} \rightarrow(\mathrm{ii})+$ dil. $\mathrm{HCl} \rightarrow(\mathrm{iii})+$ Conc. $\mathrm{H}_3 \mathrm{PO}_4 \rightarrow(\mathrm{iv})$
A

B
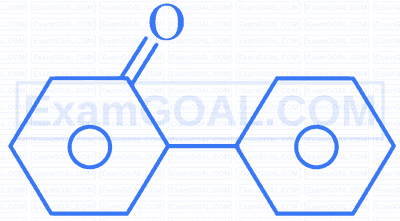
C
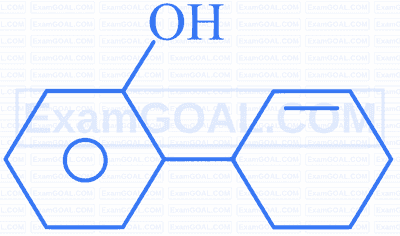
D

3
COMEDK 2025 Morning Shift
MCQ (Single Correct Answer)
+1
-0
Match the structures in Column I with their correct IUPAC names given in Column II.
| Column I | Column II | ||
|---|---|---|---|
| A. |  |
P. | 2,3-Dibromo-1-phenylpentane. |
| B. | 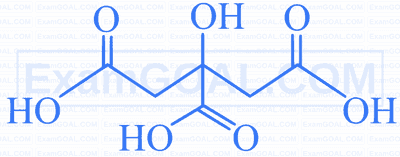 |
Q. | 2,3- Dibromohexanedial. |
| C. |  |
R. | 2- ( 4- isobutylphenyl) propanoic acid |
| D. |  |
S. | 2- Hydroxy-1,2,3- propanetricarboxylic acid. |
A
$\mathrm{A}=\mathrm{Q} \quad \mathrm{B}=\mathrm{P} \quad \mathrm{C}=\mathrm{S} \quad \mathrm{D}=\mathrm{R}$
B
$\mathrm{A}=\mathrm{R} \quad \mathrm{B}=\mathrm{S} \quad \mathrm{C}=\mathrm{Q} \quad \mathrm{D}=\mathrm{P}$
C
$\mathrm{A}=\mathrm{S} \quad \mathrm{B}=\mathrm{R} \quad \mathrm{C}=\mathrm{Q} \quad \mathrm{D}=\mathrm{P}$
D
$\mathrm{A}=\mathrm{S} \quad \mathrm{B}=\mathrm{R} \quad \mathrm{C}=\mathrm{P} \quad \mathrm{D}=\mathrm{Q}$
4
COMEDK 2025 Morning Shift
MCQ (Single Correct Answer)
+1
-0
Identify $[\mathrm{X}]$, the final product formed when 2 moles of Ethanal undergoes the following series of reactions with reagents [(i) to (iv)]

A
But-3-enoic acid
B
But-2-enoic acid
C
Propanoic acid
D
Ethanoic acid
Paper analysis
Total Questions
Chemistry
59
Mathematics
60
Physics
60
COMEDK
Papers
2025
2024
2022
2021
2020