Current Electricity · Physics · NEET
MCQ (Single Correct Answer)
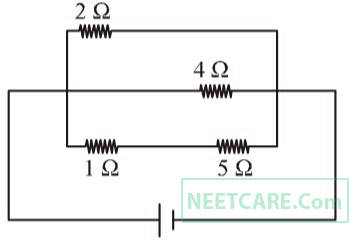
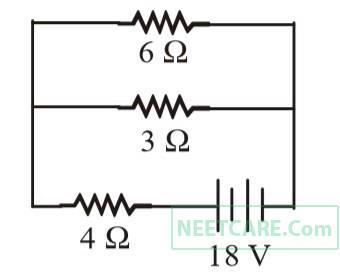
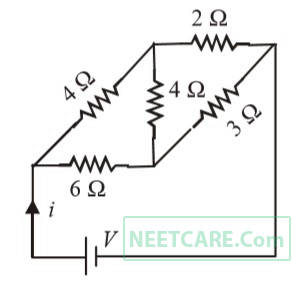
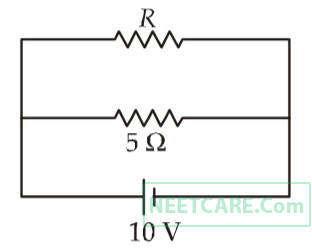
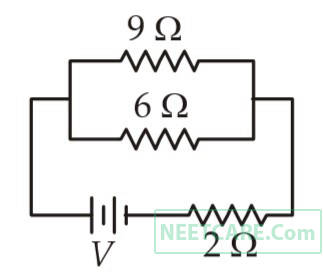
The current passing through the battery in the given circuit, is:

A wire of resistance $R$ is cut into 8 equal pieces. From these pieces two equivalent resistances are made by adding four of these together in parallel. Then these two sets are added in series. The net effective resistance of the combination is:
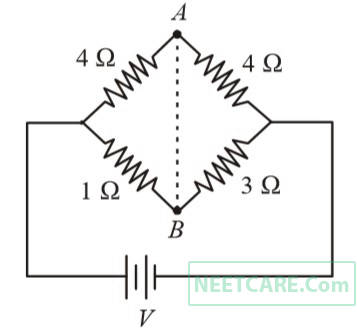
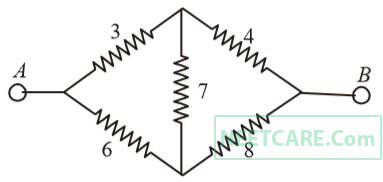
A constant voltage of 50 V is maintained between the points $A$ and $B$ of the circuit shown in the figure. The current through the branch $C D$ of the circuit is:

A uniform wire of diameter $$d$$ carries a current of $$100 \mathrm{~mA}$$ when the mean drift velocity of electrons in the wire is $$v$$. For a wire of diameter $$\frac{d}{2}$$ of the same material to carry a current of $$200 \mathrm{~mA}$$, the mean drift velocity of electrons in the wire is
A uniform metal wire of length $$l$$ has $$10 \Omega$$ resistance. Now this wire is stretched to a length $$2l$$ and then bent to form a perfect circle. The equivalent resistance across any arbitrary diameter of that circle is
The given circuit shows a uniform straight wire $$A B$$ of $$40 \mathrm{~cm}$$ length fixed at both ends. In order to get zero reading in the galvanometer $$G$$, the free end of $$J$$ is to be placed from $$B$$ at:

The terminal voltage of the battery, whose emf is $$10 \mathrm{~V}$$ and internal resistance $$1 \Omega$$, when connected through an external resistance of $$4 \Omega$$ as shown in the figure is:

A wire of length '$$l$$' and resistance $$100 \Omega$$ is divided into 10 equal parts. The first 5 parts are connected in series while the next 5 parts are connected in parallel. The two combinations are again connected in series. The resistance of this final combination is:
Two heaters $$A$$ and $$B$$ have power rating of $$1 \mathrm{~kW}$$ and $$2 \mathrm{~kW}$$, respectively. Those two are first connected in series and then in parallel to a fixed power source. The ratio of power outputs for these two cases is:
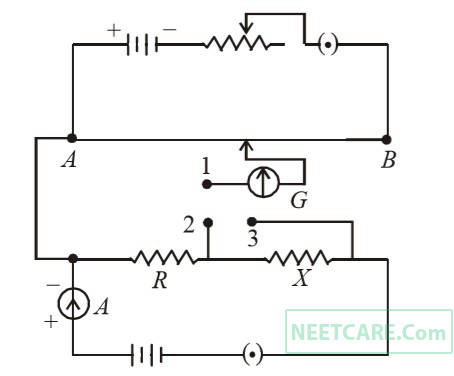
Choose the correct circuit which can achieve the bridge balance.
A certain wire $$\mathrm{A}$$ has resistance $$81 ~\Omega$$. The resistance of another wire $$\mathrm{B}$$ of same material and equal length but of diameter thrice the diameter of A will be :
A copper wire of radius $$1 \mathrm{~mm}$$ contains $$10^{22}$$ free electrons per cubic metre. The drift velocity for free electrons when $$10 \mathrm{~A}$$ current flows through the wire will be (Given, charge on electron $$=1.6 \times 10^{-19} \mathrm{C}$$ ) :
The emf of a cell having internal resistance $$1 \Omega$$ is balanced against a length of $$330 \mathrm{~cm}$$ on a potentiometer wire. When an external resistance of $$2 \Omega$$ is connected across the cell, the balancing length will be :
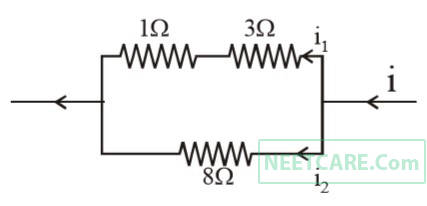
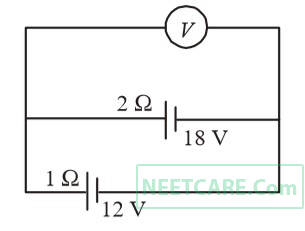
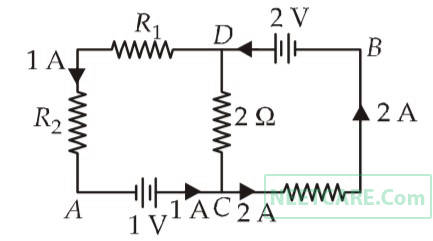
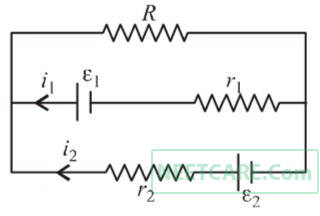
The magnitude and direction of the current in the following circuit is :-

If the galvanometer $$G$$ does not show any deflection in the circuit shown, the value of $$R$$ is given by:

Resistance of a carbon resistor determined from colour codes is $$(22000 \pm 5 \%) \Omega$$. The colour of third band must be :
The resistance of platinum wire at $$0^{\circ} \mathrm{C}$$ is $$2 ~\Omega$$ and $$6.8 ~\Omega$$ at $$80^{\circ} \mathrm{C}$$. The temperature coefficient of resistance of the wire is :
10 resistors, each of resistance $$\mathrm{R}$$ are connected in series to a battery of emf $$E$$ and negligible internal resistance. Then those are connected in parallel to the same battery, the current is increased $$n$$ times. The value of $$n$$ is :
The reciprocal of resistance is :
A cell of emf 4 V and internal resistance 0.5 $$\Omega$$ is connected to a 7.5 $$\Omega$$ external resistance. The terminal potential difference of the cell is
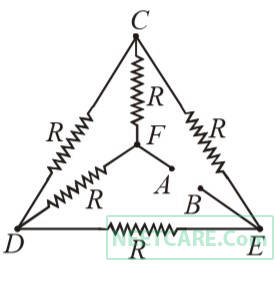
The equivalent resistance of the infinite network given below is :

The sliding contact C is at one fourth of the length of the potentiometer wire (AB) from A as shown in the circuit diagram. If the resistance of the wire AB is R0, then the potential drop (V) across the resistor R is

Two resistors of resistance, 100 $$\Omega$$ and 200 $$\Omega$$ are connected in parallel in an electrical circuit. The ratio of the thermal energy developed in 100 $$\Omega$$ to that in 200 $$\Omega$$ in a given time is
A copper wire of length 10 m and radius $$\left( {{{{{10}^{ - 2}}} \over {\sqrt \pi }}} \right)$$ m has electrical resistance of 10 $$\Omega$$. The current density in the wire for an electric field strength of 10 (V/m) is
A wheatstone bridge is used to determine the value of unknown resistance X by adjusting the variable resistance Y as shown in the figure. For the most precise measurement of X, the resistance P and Q

| Column - I | Column - II | ||
|---|---|---|---|
| (A) | Drift Velocity | (P) | $${m \over {n{e^2}p}}$$ |
| (B) | Electrical Resistivity | (Q) | $$ne{\upsilon _d}$$ |
| (C) | Relaxation Period | (R) | $${{eE} \over m}\tau $$ |
| (D) | Current Density | (S) | $${E \over J}$$ |
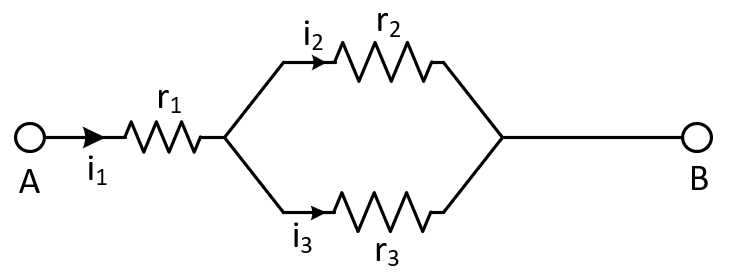

The values of resistance and tolerance, respectively, are
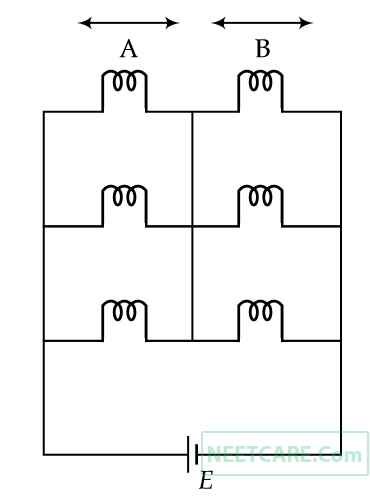
The ratio of power consumption by the bulbs when (i) all are glowing and (ii) in the situation when two from section A and one from section B are glowing, will be :
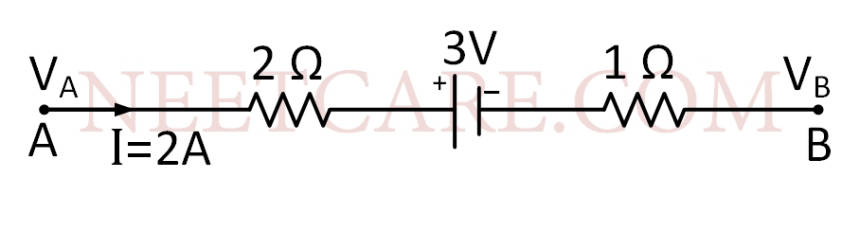
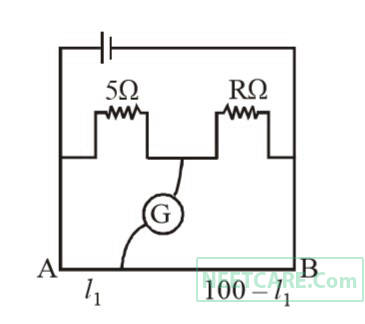
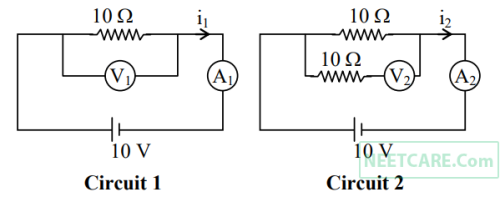
the balancing lengths on the potentiometer wire are found to be 3 m and 2.85 m, respectively. The value of internal resistance of the cell is
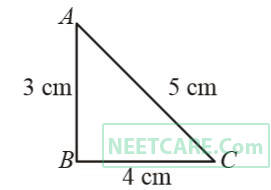
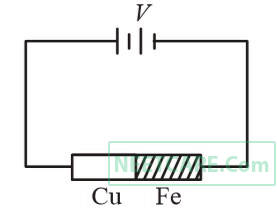
How much voltage is required to produce a current of 1 ampere in the rods?
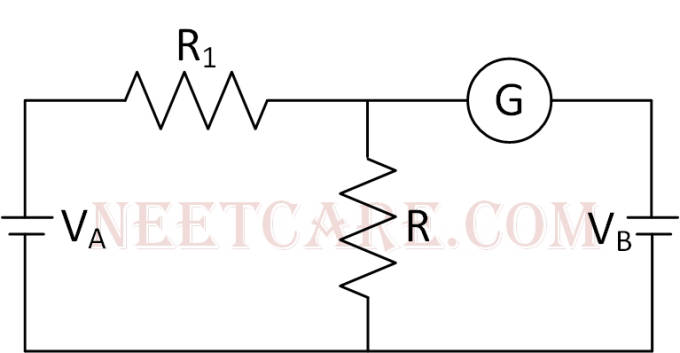
(A) Kirchoff's junction law follows from the conservation of charge.
(B) Kirchhoff's loop law follows from the conservation of energy.
Which of the following is correct?

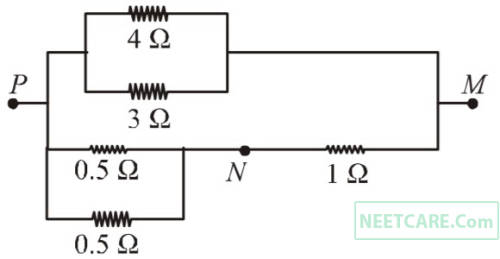
In the circuit shown, the current through the 4 $$\Omega $$ resistor is 1 amp when the points P and M are connected to a d.c. voltage source. The potential difference betwen the points M and N is