AP EAPCET 2024 - 20th May Morning Shift

Paper was held on Mon, May 20, 2024 3:30 AM

Chemistry

The angular momentum of an electron in a stationary state of $\mathrm{Li}^{2+}(Z=3)$ is $3 h / \pi$. The radius and energy of that stationary state are respectively

Identify the pair of elements in which number of electrons in ( $n-1$ ) shell is same

$$ \text { Match the following. } $$

$$ \text { List-I } $$		$$ \text { List-II } $$
A	$$ \text { Ionisation enthalpy } $$	I	$$ \mathrm{P}<\mathrm{Si}<\mathrm{Mg}<\mathrm{Na} $$
B	$$ \text { Metallic character } $$	II	$$ \mathrm{I}<\mathrm{N}<\mathrm{O}<\mathrm{F} $$
C	$$ \text { Electron gain enthalpy } $$	III	$$ \mathrm{B}<\mathrm{Be}<\mathrm{C}<\mathrm{O}<\mathrm{N} $$
D	$$ \text { Electronegativity } $$	IV	$$ \mathrm{l}<\mathrm{Br}<\mathrm{F}<\mathrm{Cl} $$

The correct order of bond angles of the molecules $\mathrm{SiCl}_4, \mathrm{SO}_3, \mathrm{NH}_3, \mathrm{HgCl}_2$ is

$$ \text { Observe the following structure, } $$

AP EAPCET 2024 - 20th May Morning Shift Chemistry - Chemical Bonding and Molecular Structure Question 3 English

$$ \text { The formal charges on the atoms 1,2,3 respectively are } $$

Two statement are given below.

Statement I : The ratio of the molar volume of a gas to that of an ideal gas at constant temperature and pressure is called the compressibility factor.

Statement II : The rms velocity of a gas is directly proportional to square root of $T(\mathrm{~K})$.

The correct answer is

At 133.33 K . the rms velocity of an ideal gas is $$ \left(M=0.083 \mathrm{~kg} \mathrm{~mol}^{-1} ; R=8.3 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}\right) $$

Given below are two statements.

Statement I : In the decomposition of potassium chlorate Cl is reduced.

Statement II : Reaction of Na with $\mathrm{O}_2$ to form $\mathrm{Na}_2 \mathrm{O}$ is a redox reaction.

The correct answer is

Observe the following reaction,

$$ 2 A_2(g)+B_2(g) \xrightarrow{T(\mathrm{~K})} 2 A_2 B(g)+600 \mathrm{~kJ} $$

The standard enthalpy of formation $\left(\Delta_f H^{\ominus}\right)$ of $A_2 B(g)$ is

Identify the molecule for which the enthalpy of atomisation ( $\Delta_a H^{\ominus}$ ) and bond dissociation enthalpy $\left(\Delta_{\text {bond }} H^{\ominus}\right)$ are not equal

$K_C$ for the reaction, $A_2(g) \stackrel{T(\mathrm{~K})}{\rightleftharpoons} B_2(g)$ is 99.0 . In a 1 L closed flask two moles of $B_2(g)$ is heated to $T(\mathrm{~K})$. What is the concentration of $B_2(g)\left(\right.$ in $\left.\mathrm{mol} \mathrm{L}^{-1}\right)$ at equilibrium?

At $27^{\circ} \mathrm{C}, 100 \mathrm{~mL}$ of 0.4 M HCl is mixed with 100 mL of 0.5 M NaOH solution. To the resultant solution, 800 mL of distilled water is added. What is the pH of final solution?

' $X$ ' on hydrolysis gives two products. One of them is solid. What is ' $X$ '?

$\mathrm{Ba}, \mathrm{Ca}$ and Sr form halide hydrates. Their formulae are $\mathrm{BaCl}_2 \cdot x \mathrm{H}_2 \mathrm{O}, \mathrm{CaCl}_2 \cdot y \mathrm{H}_2 \mathrm{O} \cdot \mathrm{SrCl}_2 \cdot z \mathrm{H}_2 \mathrm{O}$. The value of $x, y, z$ respectively are

The bond angles $b_1, b_2$ and $b_3$ in the given structure are respectively (in ${ }^{\circ}$ )

AP EAPCET 2024 - 20th May Morning Shift Chemistry - Chemical Bonding and Molecular Structure Question 5 English

Which of the following oxides is acidic in nature?

$$ \text { Match the following. } $$

List-I F-ion concentration in drinking water)		List-II (Effects on humans)
A	$$ \text { <1 ppm } $$	I	$$ \text { Harmful to bones } $$
B	$$ >2 \mathrm{ppm} $$	II	$$ \text { Tooth decay } $$
C	$$ >10 \mathrm{ppm} $$	III	$$ \text { Brown mottling of teeth } $$

$$ \text { Correct answer is } $$

The number of nucleophiles in the following list is

$$ \mathrm{CH}_3 \mathrm{NH}_2, \mathrm{CH}_3 \mathrm{CHO}, \mathrm{C}_2 \mathrm{H}_4, \mathrm{CH}_3 \mathrm{SH} $$

An alkene $X\left(\mathrm{C}_4 \mathrm{H}_8\right)$ on reaction with HBr gave $Y\left(\mathrm{C}_4 \mathrm{H}_9 \mathrm{Br}\right)$. Reaction of $Y$ with benzene in the presence of anhydrous $\mathrm{AlCl}_3$ gave Z which is resistant to oxidation with $\mathrm{KMnO}_4-\mathrm{KOH}$. What are $X, Y, Z$ respectively?

A solid compound is formed by atoms of $A$ (cations), $B$ (cations) and O (anions). Atoms of O form hcp lattice. Atoms of $A$ occupy $25 \%$ of tetrahedral holes and atoms of $B$ occupy $50 \%$ octahedral holes. What is the molecular formula of solid?

The density of nitric acid solution is $1.5 \mathrm{~g} \mathrm{~mL}^{-1}$. Its weight percentage is 68 . What is the approximate concentration (in $\mathrm{mol} \mathrm{L}^{-1}$ ) of nitric acid ?

$$ (\mathrm{N}=14 \mathrm{u} ; \mathrm{O}=16 \mathrm{u} ; \mathrm{H}=1 \mathrm{u}) $$

The osmotic pressure of sea water is 1.05 atm . Four experiments were carried as shown in table. In which of the following experiments, pure water can be obtained in part-II of vessel.

AP EAPCET 2024 - 20th May Morning Shift Chemistry - Liquid Solution Question 2 English

$$ \begin{aligned} &\text { Table }\\ &\begin{array}{ccc} \hline \begin{array}{c} \text { Expt. } \\ \text { No } \end{array} & \begin{array}{c} \text { Pressure applied in } \\ \text { part-1 of vessel } \end{array} & \begin{array}{c} \text { Pressure applied in } \\ \text { part-II of vessel } \end{array} \\ \hline \text { I. } & 10 \mathrm{~atm} & - \\ \hline \text { II. } & - & 10 \mathrm{~atm} \\ \hline \text { III. } & 15 \mathrm{~atm} & - \\ \hline \text { IV. } & - & 15 \mathrm{~atm} \end{array} \end{aligned} $$

Aqueous $\mathrm{CuSO}_4$ solution was electrolysed by passing 2 amp of current for 10 min . What is the weight (in g) of copper deposited at cathode ?

$$ \left(\mathrm{Cu}=63 \mathrm{u} ; F=96500 \mathrm{C} \mathrm{~mol}^{-1}\right) $$

For a first order reaction the concentration of reactant was reduced from $0.03 \mathrm{molL}^{-1}$ to $0.02 \mathrm{molL}^{-1}$ in 25 min . What is its rate (in $\mathrm{molL}^{-1} \mathrm{~s}^{-1}$ )?

' $X$ ' is a protecting colloid. The following data is obtained for preventing the coagulation of 10 mL of gold sol to which 1 mL of $10 \% \mathrm{NaCl}$ is added. What is the gold number of ' $X$ '?

$$ \begin{array}{ccl} \hline \text { Expt No. } & \begin{array}{c} \text { Weight of } X \text { (in mg) } \\ \text { added to gold sol } \end{array} & \text { Coagulation } \\ \hline 1 & 24 & \text { Not prevented } \\ \hline 2 & 23 & \text { Not prevented } \\ \hline 3 & 26 & \text { Prevented } \\ \hline 4 & 27 & \text { Prevented } \\ \hline 5 & 25 & \text { Prevented } \\ \hline \end{array} $$

Which sol is used as intramuscular injection?

The reactions which occur in blast furnace at $500-800 \mathrm{~K}$ during extraction of iron from haematite are

i. $3 \mathrm{Fe}_2 \mathrm{O}_3+\mathrm{CO} \longrightarrow 2 \mathrm{Fe}_3 \mathrm{O}_4+\mathrm{CO}_2$

ii. $\mathrm{Fe}_2 \mathrm{O}_3+3 \mathrm{C} \longrightarrow 2 \mathrm{Fe}+3 \mathrm{CO}$

iii. $\mathrm{Fe}_3 \mathrm{O}_4+4 \mathrm{CO} \longrightarrow \mathrm{Fe}+4 \mathrm{CO}_2$

iv. $\mathrm{Fe}_2 \mathrm{O}_3+\mathrm{CO} \longrightarrow 2 \mathrm{FeO}+\mathrm{CO}_2$

Which of the following reactions give phosphine?

i. Reaction of calcium phosphide with water

ii. Heating white phosphorous with concentrated NaOH solution in inert atmosphere

iii. Heating red phosphorous with alkali

Which transition metal does not form 'MO' type oxide? ( $M=$ transition metal)

The paramagnetic complex ion, which has no unpaired electrons in $t_{2 g}$ orbitals is

$$ \text { Which of the following is an example for fibre? } $$

When glucose is oxidised with nitric acid the compound formed is

The number of essential and non-essential amino acids from the following list respectively is Val, Gly, Leu, Lys, Pro, Ser

Which of the following pair is not correctly matched?

An alkene $X\left(\mathrm{C}_4 \mathrm{H}_8\right)$ does not exhibit cis-trans is memerisn Reaction of $X$ with $\mathrm{Br}_2$ in the presence of UV light gane $Y$. What is $Y$ ?

The two reactions involved in the conversion of benzene diazonium chloride to diphenyl are respectively

$$ \text { Consider the reactions, } $$

AP EAPCET 2024 - 20th May Morning Shift Chemistry - Aldehyde and Ketone Question 2 English

Consider the following reactions,

AP EAPCET 2024 - 20th May Morning Shift Chemistry - Alcohol, Phenols and Ethers Question 1 English

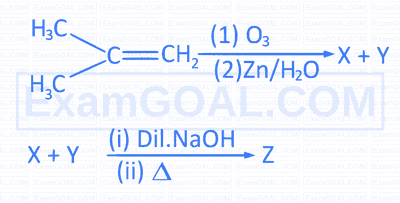
$Y$ and $Z$ respectively are

$$ \text { The incorrect statement about ' } B \text { ' is } $$

AP EAPCET 2024 - 20th May Morning Shift Chemistry - Aldehyde and Ketone Question 1 English

$$ \text { The incorrect statement about } B \text { is } $$

$$ \text { Benzamide } \xrightarrow{\mathrm{Br}_2 / \mathrm{NaOH}} X \xrightarrow[\text { Alc. } \mathrm{KOH}]{\mathrm{CHCl}_3} Y $$

The conversion of $X$ to $Y$ is

Mathematics

Let $f(x)=3+2 x$ and $g_n(x)=(f \circ f \circ f o \ldots$ in times $)(x)$, $\forall n \in N$ if all the lines $y=g_n(x)$ pass through a fixed point $(\alpha, \beta)$, then $\alpha+\beta=$

Let $a > 1$ and $0 < \mathrm{b} < 1$. If $f: R \rightarrow[0,1]$ is defined by $f(x)=\left\{\begin{array}{ll}a^x, & -\infty < x < 0 \\ b^x, & 0 \leq x < \infty\end{array}\right.$, then $f(x)$ is

$ \frac{1}{3 \cdot 7}+\frac{1}{7 \cdot 11}+\frac{1}{11 \cdot 15}+\ldots$ to 50 terms $=$

$$ \text { If } A=\left[\begin{array}{lll} 1 & 0 & 2 \\ 2 & 1 & 3 \\ 3 & 2 & 4 \end{array}\right] \text {, then } A^2-5 A+6 I= $$

Sum of the positive roots of the equation $$ \left|\begin{array}{ccc} x^2+2 x & x+2 & 1 \\ 2 x+1 & x-1 & 1 \\ x+2 & -1 & 1 \end{array}\right|=0 \text { is } $$

If the solution of the system of simultaneous linear equations $x+y-z=6,3 x+2 y-z=5$ and $2 x-y-2 z+3=0$ is $x=\alpha, y=\beta, z=y$, then $\alpha+\beta=$

If the point $P$ represents the complex number $z=x+i y$ in the argand plane and if $\frac{z+i}{z-i}$ is a purely imaginary number, then the locus of $P$ is

$S=\{z \in C /|z+1-i|=1\}$ represents

If $\cos \alpha+\cos \beta+\cos \gamma=\sin \alpha+\sin \beta+\sin \gamma=0$, then $\left(\cos ^3 \alpha+\cos ^3 \beta+\cos ^3 \gamma\right)^2+\left(\sin ^3 \alpha+\sin ^3 \beta+\sin ^3 \gamma\right)^2=$

If $\alpha$ and $\beta$ are two double roots of $x^2+3(a+3) x-9 a=0$ for different values of $a(\alpha>\beta)$, then the minimum value of $x^2+\alpha x-\beta=0$ is

If $2 x^2+3 x-2=0$ and $3 x^2+\alpha x-2=0$ have one common root, then the sum of all possible values of $\alpha$ is

If the sum of two roots of $x^3+p x^2+q x-5=0$ is equal to its third root, then $p\left(p^2-4 q\right)=$

If $P(x)=x^5+a x^4+b x^3+c x^2+d x+e$ is a polynomial such that $P(0)=1, P(1)=2, P(2)=5, P(3)=10$ and $P(4)=17$, then $P(5)=$

If a polygon of $n$ sides has 275 diagonals, then $n$ is

The number of positive divisors of 1080 is

If $a_n=\sum\limits_{r=0}^n \frac{1}{{ }^n C_r}$, then $\sum\limits_{r=0}^n \frac{r}{{ }^n C_r}=$

The coefficient of $x^5$ in the expansion of $\left(2 x^3-\frac{1}{3 x^2}\right)^5$ is

$$1+\frac{1}{3}+\frac{1 \cdot 3}{3 \cdot 6}+\frac{1 \cdot 3 \cdot 5}{3 \cdot 6 \cdot 9}+\ldots \text { to } \infty= $$

If $\frac{A}{x-a}+\frac{B x+C}{x^2+b^2}=\frac{1}{(x-a)\left(x^2+b^2\right)}$, then $\mathrm{C}=$

If $\cos ^4 \frac{\pi}{8}+\cos ^4 \frac{3 \pi}{8}+\cos ^4 \frac{5 \pi}{8}+\cos ^4 \frac{7 \pi}{8}=k$, then $\sin ^{-1}\left(\sqrt{\frac{k}{2}}\right)+\cos ^{-1}\left(\frac{k}{3}\right)=$

$$ \text { } \frac{\cos 10^{\circ}+\cos 80^{\circ}}{\sin 80^{\circ}-\sin 10^{\circ}}= $$

$\frac{\sin 1^{\circ}+\sin 2^{\circ}+\ldots . . .+\sin 89^{\circ}}{2\left(\cos 1^{\circ}+\cos 2^{\circ}+\ldots+\cos 44^{\circ}\right)+1}=$

The number of ordered pairs $(x, y)$ satisfying the equations $\sin x+\sin y=\sin (x+y)$ and $|x|+|y|=1$ is

$$4 \tan ^{-1} \frac{1}{5}-\tan ^{-1} \frac{1}{70}+\tan ^{-1} \frac{1}{99}=$$

If $5 \sin h x-\cos h x=5$, then one of the values of $\tan h x$ is

In $\triangle A B C$, if $r_1=4, r_2=8$ and $r_3=24$, then $a=$

If a circle is inscribed in an equilateral triangle of side $a$, then the area of any square (in sq units) inscribed in this circle is

Match the items of List I with those of List II (here, $\Delta$ denotes the area of $\triangle A B C$ )

List I		List II
(A)	$$ \sum \cot A $$	(i)	$$ (a+b+c)^2 \frac{1}{4 \Delta} $$
(B)	$$ \sum \cot \frac{A}{2} $$	(ii)	$$ \left(a^2+b^2+c^2\right) \frac{1}{4 \Delta} $$
(C)	If $\tan A: \tan B: \tan C=1: 2: 3$, then $\sin A: \sin B: \sin C=$	(iii)	$$ 8: 6: 5 $$
(D)	$$ \begin{aligned} &\text { If } \cot \frac{A}{2}: \cot \frac{B}{2}: \cot \frac{C}{2}=3: 7: 9\\ &\text { then } a: b: c= \end{aligned} $$	(iv)	$$ 12: 5: 13 $$
		(v)	$$ \sqrt{5}: 2 \sqrt{2}: 3 $$
		(vi)	$$ 4 \Delta $$

$$ \text { Then, the correct match is } $$

Let $O(\mathbf{O}), A(\hat{\mathbf{i}}+2 \hat{\mathbf{j}}+\hat{\mathbf{k}}), B(-2 \hat{\mathbf{i}}+3 \hat{\mathbf{k}}), C(2 \hat{\mathbf{i}}+\hat{\mathbf{j}})$ and $D(4 \hat{\mathbf{k}})$ are position vectors of the points $O, A, B, C$ and $D$. If a line passing through $A$ and $B$ intersects the plane passing through $O, C$ and $D$ at the point $R$, then position vector of $R$ is

$\mathbf{a}, \mathbf{b}, \mathbf{c}$ are non-coplanar vectors. If $\alpha \mathbf{d}=\mathbf{a}+\mathbf{b}+\mathbf{c}$ and $\beta \mathbf{a}=\mathbf{b}+\mathbf{c}+\mathbf{d}$, then $|\mathbf{a}+\mathbf{b}+\mathbf{c}+\mathbf{d}|=$

$\mathbf{u}, \mathbf{v}$ and $\mathbf{w}$ are three unit vectors. Let $\hat{\mathbf{p}}=\hat{\mathbf{u}}+\hat{\mathbf{v}}+\hat{\mathbf{w}} \cdot \hat{\mathbf{q}}=\hat{\mathbf{u}} \times(\hat{\mathbf{v}} \times \hat{\mathbf{w}})$. If $\hat{\mathbf{p}} \cdot \hat{\mathbf{u}}=\frac{3}{2} \cdot \hat{\mathbf{p}} \hat{\mathbf{v}}=\frac{7}{4}|\hat{\mathbf{p}}|=2$ and $v=K . q$, then $K=$

The distance of the point $O(\mathbf{O})$ from the plane $\mathbf{r}$. $(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}})=5$ measured parallel to $2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}-6 \hat{\mathbf{k}}$ is

If $\mathbf{a}$ and $\mathbf{b}$ are the two non collinear vectors, then $|\mathbf{b}|\mathbf{a}+|\mathbf{a}| \mathbf{b}$ represents

$x$ and $y$ are the arithmetic means of the runs of two batsmen $A$ and $B$ in 10 innings respectively and $\sigma_A, \sigma_B$ are the standard deviations of their runs in them. If batsman $A$ is more consistent than $B$, then he is also a higher run scorer only when

S is the sample space and $A, B$ are two events of a random experiment. Match the items of List $A$ with the items of List B

$$ \text { List A } $$		$$ \text { List B } $$
I	$A, B$ are mutually exclusive events	a.	$$ P(A \cap B)=P(B)-P(\bar{A}) $$
II	$$ A, B \text { are independent events } $$	b.	$$ P(A) \leq P(B) $$
III	$$ A \cap B=A $$	c.	$$ P\left(\frac{\bar{A}}{B}\right)=1-P(A) $$
IV	$$ A \cup B=S $$	d.	$$ P(A \cup B)=P(A)+P(B) $$
		e.	$$ P(A)+P(B)=2 $$

$P(A \mid A \cap B)+P(B \mid A \cap B)=$

Two digits are selected at random from the digits 1 through 9. If their sum is even, then the probability that both are odd, is

A, B and C are mutually exclusive and exhaustive events of a random experiment and $E$ is an event that occurs in conjunction with one of the events $\mathrm{A}, \mathrm{B}$ and $C$. The conditional probabilities of $E$ given the happening of $A, \mathrm{~B}$ and C are respectively $0.6,0.3$ and 0.1. If $P(A)=0.30$ and $P(B)=0.50$, then $P(C / E)=$

For the probability distribution of a discrete random variable $X$ as given below, then mean of $X$ is

X = x	-2	-1	0	1	2	3
P(X = x)	$$ \frac{1}{10} $$	$$ K+\frac{2}{10} $$	$$ K+\frac{3}{10} $$	$$ K+\frac{3}{10} $$	$$ K+\frac{4}{10} $$	$$ K+\frac{2}{10} $$

In a random experiment, two dice are thrown and the sum of the numbers appeared on them is recorded. This experiment is repeated 9 times. If the probability that a sum of 6 appears atleast once is $P_1$ and a sum of 8 appears atleast once is $P_2$, then $P_1: P_2=$

If the line segment joining the points $(1,0)$ and $(0,1)$ subtends an angle of $45^{\circ}$ at a variable point $P$, then the equation of the locus of $P$ is

If the origin is shifted to a point $P$ by the translationd axes to remove the $y$-term from the equation $x^2-y^2+2 y-1=0$, then the transformed equation of it is

A line $L$ intersects the lines $3 x-2 y-1=0$ and $x+2 y+1=0$ at the points $A$ and $B$. If the point $(1,2)$ bisects the line segment $A B$ and $\frac{x}{a}+\frac{y}{b}=1$ is the equation of the line $L$, then $a+2 b+1=$

A line $L$ passing through the point $(2,0)$ makes an angle $60^{\circ}$ with the line $2 x-y+3=0$. If $L$ makes an acute angle with the positive X-axis in the anti-clockwise direction, then the $Y$-intercept of the line $L$ is

If the slope of one line of the pair of lines $2 x^2+h x y+6 y^2=0$ is thrice the slope of the other line, then $h=$

If the equation of the pair of straight lines passing through the point $(1,1)$ and perpendicular to the pair of lines $3 x^2+11 x y-4 y^2=0$ is $a x^2+2 h x y+b y^2+2 g x+2 f y+12=0$, then $2(a-h+b-g+f-12)=$

Equation of the circle having its centre on the line $2 x+y+3=0$ and having the lines $3 x+4 y-18=0,3 x+4 y+2=0$ as tangents is

If power of a point $(4,2)$ with respect to the circle $x^2+y^2-2 \alpha x+6 y+\alpha^2-16=0$ is 9 , then the sum of the lengths of all possible intercepts made by such circles on the coordinate axes is

Let $\alpha$ be an integer multiple of 8 . If $S$ is the set of all possible values of $\alpha$ such that the line $6 x+8 y+\alpha=0$ intersects the circle $x^2+y^2-4 x-6 y+9=0$ at two distinct points, then the number of elements in $S$ is

If the circle $x^2+y^2-8 x-8 y+28=0$ and $x^2+y^2-8 x-6 y+25-\alpha^2=0$ have only one common tangent, then $\alpha=$

If the equation of the circle passing through the points of intersection of the circles $x^2-2 x+y^2-4 y-4=0$, $x^2+2 x+y^2+4 y-4=0$ and the point $(3,3)$ is given by $x^2+y^2+\alpha x+\beta y+\gamma=0$, then $3(\alpha+\beta+\gamma)=$

A common tangent to the circle $x^2+y^2=9$ and parabola $y^2=8 x$ is

Let F and $F^1$ be the foci of the ellipse $\frac{x^2}{4}+\frac{y^2}{b^2}=1(b<2)$ and $B$ is one end of the minor axis. If the area of the triangle $\mathrm{FBF}^1$ is $\sqrt{3}$ sq units, then the eccentricity of the ellipse is

If a circle of radius 4 cm passes through the foci of the hyperbola $\frac{x^2}{a^2}-\frac{y^2}{4}=1$ and concentric with the hyperbola, then the eccentricity of the conjugate hyperbola of that hyperbola is

If a tangent to the hyperbola $x^2-\frac{y^2}{3}=1$ is also a tangent to the parabola $y^2=8 x$, then equation of such tangent with the positive slope is

If $A(1,0,2), B(2,1,0), C(2,-5,3)$ and $D(0,3,2)$ are four points and the point of intersection of the lines $A B$ and $C D$ is $P(a, b, c)$, then $a+b+c=$

The direction cosines of two lines are connected by the relations $l+m-n=0$ and $l m-2 m n+n l=0$. If $\theta$ is the acute angle between those lines, then $\cos \theta=$

The distance from a point $(1,1,1)$ to a variable plane $\pi$ is 12 units and the points of intersections of the plane $\pi$ and $X, Y, Z$ - axes are $A, B, C$ respectively, If the point of intersection of the planes through the points $A, B, C$ and parallel to the coordinate planes is $P$, then the equation of the locus of $P$ is

$\lim \limits_{x \rightarrow 0} \frac{\sqrt{1+\sqrt{1+x^4}}-\sqrt{2+x^5+x^6}}{x^4}=$

$\lim \limits_{x \rightarrow 1} \frac{\sqrt{x}-1}{\left(\cos ^{-1} x\right)^2}=$

If a function $f(x)=\left\{\begin{array}{cl}\frac{\tan (\alpha+1) x+\tan 2 x}{x} & \text { if } x>0 \\ \beta & \text { at } x=0 \text { is } \\ \frac{\sin 3 x-\tan 3 x}{x^3} & \text { if } x<0\end{array}\right.$

continuous at $x=0$, then $|\alpha|+|\beta|=$

If $y=\tan (\log x)$, then $\frac{d^2 y}{d x^2}=$

For $x<0, \frac{d}{d x}\left[|x|^x\right]=$

If $y=x-x^2$, then the rate of change of $y^2$ with respect to $x^2$ at $x=2$ is

If $T=2 \pi \sqrt{\frac{L}{g}}, \mathrm{~g}$ is a constant and the relative error in $T$ is $k$ times to the percentage error in $l$, then $\frac{1}{K}=$

The angle between the curves $y^2=2 x$ and $x^2+y^2=8$ is

If the function $f(x)=\sqrt{x^2-4}$ satisfies the Lagrange's mean value theorem on $[2,4]$, then the value of $C$ is

If $x, y$ are two positive integers such that $x+y=20$ and the maximum value of $x^3 y$ is $k$ at $x=\alpha$ and $y=\beta$, then $\frac{k}{\alpha^2 \beta^2}=$

$\int \frac{2 x^2-3}{\left(x^2-4\right)\left(x^2+1\right)} d x=A \tan ^{-1} x+B \log (x-2)+C \log (x+2)$, then $6 A+7 B-5 C=$

$\int \frac{3 x^9+7 x^8}{\left(x^2+2 x+5 x^8\right)^2} d x=$

$\int \frac{\cos x+x \sin x}{x(x+\cos x)} d x=$

If $\int \sqrt{\frac{2}{1+\sin x}} d x=2 \log |A(x)-B(x)|+C$ and $0 \leq x \leq \frac{\pi}{2}$, then $B\left(\frac{\pi}{4}\right)=$

$$ \begin{aligned} &\text { If } \int \frac{3}{2 \cos ^3 x \sqrt{2 \sin 2 x}} d x=\frac{3}{2}(\tan x)^B+\frac{3}{10}(\tan x)^A+C \text {, than }\\&A= \end{aligned} $$

$\int_{-\pi}^\pi \frac{x \sin ^3 x}{4-\cos ^2 x} d x=$

$$ \text { } \int\limits_{-3}^3|2-x| d x= $$

$$ \int_{\frac{1}{\sqrt[5]{31}}}^{\frac{1}{\sqrt[5]{242}}} \frac{1}{\sqrt[5]{x^{30}+x^{25}}} d x= $$

Area of the region (in sq units) enclosed by the curves $y^2=8(x+2), y^2=4(1-x)$ and the $Y$-axis is

The sum of the order and degree of the differential equation $\frac{d^4 y}{d x^4}=\left\{c+\left(\frac{d y}{d x}\right)^2\right\}^{3 / 2}$ is

$$ \begin{aligned} &\text { The general solution of the differential equation }\\ &(x+y) y d x+(y-x) x d y=0 \text { is } \end{aligned} $$

The general solution of the differential equation $\left(y^2+x+1\right) d y=(y+1) d x$ is

Physics

E, M, L, G represent energy, mass, angular momentum and gravitational constant, respectively. The dimensions of $\frac{E L^2}{M^5 G^2}$ will be that of

A body starting from rest moving with an acceleration of $\frac{5}{4} \mathrm{~ms}^{-2}$. The distance travelled by the body in the third second is

A projectile can have the same range $R$ for two angles of projection. Their initial velocities are same. If $T_1$ and $T_2$ are times of flight in two cases, then the product of two times of flight is directly proportional to

If $|\mathbf{P}+\mathbf{Q}|=|\mathbf{P}|=|\mathbf{Q}|$ then the angle between $\mathbf{P}$ and $\mathbf{Q}$ is

A $4 \mathrm{~kg}$ mass is suspended as shown in figure. All pulleys are frictionless and spring constant $k$ is $8 \times 10^3 \mathrm{Nm}^{-1}$. The extension in spring is $\left(g=10 \mathrm{~ms}^{-2}\right)$

AP EAPCET 2024 - 20th May Morning Shift Physics - Work, Energy and Power Question 3 English

A 3 kg block is connected as shown in the figure. Spring constants of two springs $k_1$ and $k_2$ are $50 \mathrm{Nm}^{-1}$ and $150 \mathrm{Nm}^{-1}$ respectively. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest position is $\left(g=10 \mathrm{~ms}^{-2}\right)$

AP EAPCET 2024 - 20th May Morning Shift Physics - Simple Harmonic Motion Question 5 English

Two bodies $A$ and $B$ of masses $2 m$ and $m$ are projected vertically upwards from the ground with velocities $u$ and $2 u$ respectively. The ratio of the kinetic energy of body $A$ and the potential energy of body $B$ at height equal to half of the maximum height reached by body $A$ is

A body of mass 2 kg collides head on with another body of mass 4 kg . If the relative velocities of the bodies before and after collision are $10 \mathrm{~ms}^{-1}$ and $4 \mathrm{~ms}^{-1}$ respectively. The loss of kinetic energy of the system due to the collision is

The moment of inertia of a solid sphere of mass 20 kg and diameter 20 cm about the tangent to the sphere is

A wooden plank of mass 90 kg and length 3.3 m is floating on still water. A girl of mass 20 kg walks from one end to the other end of the plank. The distance through which the plank moves is

In a time of 2 s , the amplitude of a damped oscillator becomes $\frac{1}{e}$ times, its initial amplitude $A$. In the next two second, the amplitude of the oscillator is

A particle is executing simple harmonic motion with a time period of 3 s . At a position where the displacement of the particle is $60 \%$ of its amplitude. The ratio of the kinetic and potential energies of the particle is

The acceleration due to gravity at a height of 6400 km from the surface of the earth is $2.5 \mathrm{~ms}^{-2}$. The acceleration due to gravity at a height of 12800 km from the surface of the earth is (Radius of the earth= 6400 km )

When the load applied to a wire is increased from 5 kg wt to 8 kg wt . The elongation of the wire increases from 1 mm to 1.8 mm . The work done during the elongation of the wire is (acceleration due to gravity $=10 \mathrm{~ms}^{-2}$ )

The radius of cross-section of the cylindrical tube of a spray pump is 2 cm . One end of the pump has 50 fine holes each of radius 0.4 mm . If the speed of flow of the liquid inside the tube is $0.04 \mathrm{~ms}^{-2}$. The speed of ejection of the liquid from the holes is

The temperature difference across two cylindrical rods $A$ and $B$ of same material and same mass are $40^{\circ} \mathrm{C}$ and $60^{\circ} \mathrm{C}$ respectively. In steady state, if the rates of flow of heat through the rods $A$ and $B$ are in the ratio 3:8, the ratio of the length of the rods $A$ and $B$ is

The efficiency of Carnot cycle is $\frac{1}{6}$. By lowering the temperature of sink by 65 K , it increases to $\frac{1}{3}$. The initial and final temperature of the sink are

In a cold storage ice melts at the rate of 2 kg per hour when the external temperature is $20^{\circ} \mathrm{C}$. The minimum power output of the motor used to drive the refrigerator which just prevents the ice from melting is (latent heat of fusion of ice $=80 \mathrm{calg}^{-1}$ )

A Carnot engine has the same efficiency between 800 K and 500 K and $x>600 \mathrm{~K}$ and 600 K . The value of $x$ is

When the temperature of a gas is raised from $27^{\circ} \mathrm{C}$ to $90^{\circ} \mathrm{C}$. The increase in the rms velocity of the gas molecule is

If the frequency of a wave is increased by $25 \%$, then the change in its wavelength is (medium not changed)

An object lying 100 cm inside water is viewed normally from air. If the refractive index of water is $\frac{4}{3}$, then the apparent depth of the object is

In Young's double slit experiment two slits are placed 2 mm from each other. Interference pattern is observed on a screen placed 2 m from the plane of the slits. Then the fringe width for a light of wavelength 400 nm is

Two spheres $A$ and $B$ of radii 4 cm and 6 cm are given charges of $80 \mu \mathrm{C}$ and $40 \mu \mathrm{C}$ respectively. If they are connected by a fine wire, the amount of charge flowing from one to the other is

The angle between the electric dipole moment of a dipole and the electric field strength due to it on the equatorial line is

Two condensers $C_1$ and $C_2$ in a circuit are joined as shown in the figure. The potential of point $A$ is $V_1$ and that of point $B$ is $V_2$. The potential at point $D$ will be