WB JEE 2021
Paper was held on
Sat, Jul 17, 2021 4:30 AM
Chemistry
1
The exact order of boiling points of the compounds n-pentane, isopentane, butanone and 1-butanol is
2
The maximum number of atoms that can be in one plane in the molecule p-nitrobenzonitrile are
3
Cyclo [18] carbon is an allotrope of carbon with molecular formula C18. It is a ring of 18 carbon atoms, connected by single and triple bonds. The total number of triple bonds present in this cyclocarbon are
4
p-nitro-N, N-dimethylaniline cannot be represented by the resonating structures.
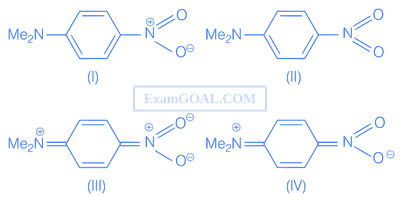

5
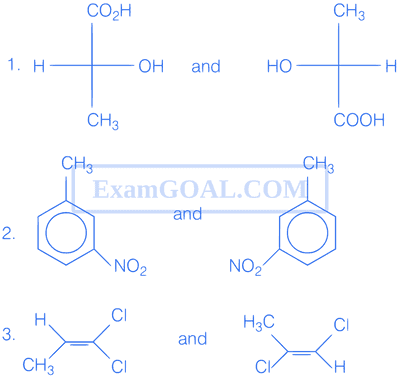
The relationship between the pair of compounds shown above are respectively
6
The exact order of acidity of the compounds p-nitrophenol, acetic acid, acetylene and ethanol is
7
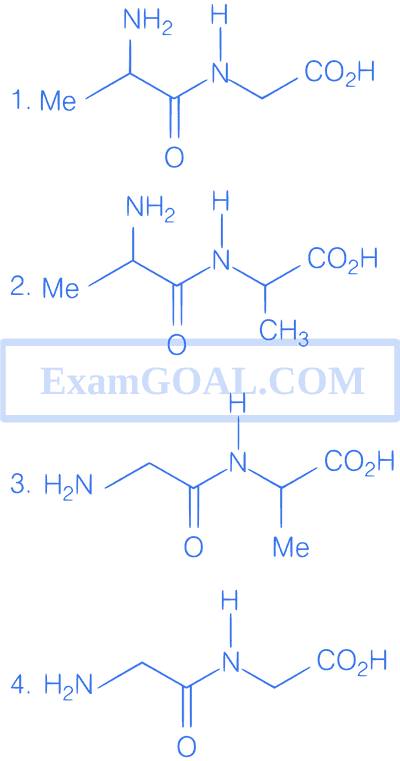
The dipeptides which may be obtained from the amino acids glycine, and alanine are
8

The compounds A and B above are respectively.
9
For a spontaneous reaction at all temperatures which of the following is correct?
10
A given amount of Fe2+ is oxidised by x mol of $$MnO_4^ - $$ in acidic medium. The number of moles of $$C{r_2}O_7^{2 - }$$ required to oxidise the same amount of Fe2+ in acidic medium is
11
An element crystallises in a body centered cubic lattice. The edge length of the unit cell is 200 pm and the density of the element is 5.0 g cm$$-$$3. Calculate the number of atoms in 100 g of this element.
12
Molecular velocities of two gases at the same temperature (T) are u1 and u2. Their masses are m1 and m2 respectively. Which of the following expressions is correct at temperature T?
13
When 20 g of naphthoic acid (C11H8O2) is dissolved in 50 g of benzene, a freezing point depression of 2K is observed. The van't Hoff factor (i) is [Kf = 1.72 K kg mol$$-$$1]
14
The equilibrium constant for the reaction
N2(g) + O2(g) $$\rightleftharpoons$$ 2NO(g) is 4 $$\times$$ 10$$-$$4 at 2000 K. In presence of a catalyst the equilibrium is attained 10 times faster. Therefore, the equilibrium constant, in presence of the catalyst at 2000 K is
N2(g) + O2(g) $$\rightleftharpoons$$ 2NO(g) is 4 $$\times$$ 10$$-$$4 at 2000 K. In presence of a catalyst the equilibrium is attained 10 times faster. Therefore, the equilibrium constant, in presence of the catalyst at 2000 K is
15
Under the same reaction conditions, initial concentration of 1.386 mol dm$$-$$3 of a substance becomes half in 40 s and 20 s through first-order and zero-order kinetics respectively. Ratio $$\left( {{{{k_1}} \over {{k_0}}}} \right)$$ of the rate constants for first-order (k1) and zero-order (k0) of the reactions is
16
Which of the following solutions will have highest conductivity?
17
Indicate the products (X) and (Y) in the following reactions
Na2S + nS(n = 1 $$-$$ 8) $$\to$$ (X)
Na2SO3 + S $$\to$$ (Y)
Na2S + nS(n = 1 $$-$$ 8) $$\to$$ (X)
Na2SO3 + S $$\to$$ (Y)
18
2.5 mL 0.4 M weak monoacidic base (Kb = 1 $$\times$$ 10$$-$$12 at 25$$^\circ$$C) is titrated with 2/15 M HCl in water at 25$$^\circ$$C. The concentration of H+ at equivalence point is (Kw = 1 $$\times$$ 10$$-$$14, at 25$$^\circ$$C)
19
Solubility products (Ksp) of the salts of types MX, MX2 and M3X at temperature T are 4.0 $$\times$$ 10$$-$$8, 3.2 $$\times$$ 10$$-$$14 and 2.7 $$\times$$ 10$$-$$15 respectively. Solubilities (in mol dm$$-$$3) of the salts at temperature T are in the order.
20
The reduction potential of hydrogen half-cell will be negative if
21
A saturated solution of BaSO4 at 25$$^\circ$$C is 4 $$\times$$ 10$$-$$5 M. The solubility of BaSO4 in 0.1 M Na2SO4 at this temperature will be
22
A solution is made by a concentrated solution of Co(NO3)2 with a concentrated solution of NaNO2 is 50% acetic acid. A solution of a salt containing metal M is added to the mixture, when a yellow precipitate is formed. Metal 'M' is
23
Extraction of a metal (M) from its sulphide ore (M2S) involves the following chemical reactions
$$2{M_2}S + 3{O_2}\buildrel {Heat} \over \longrightarrow 2{M_2}O + 2S{O_2} \uparrow $$
$${M_2}S + 2{M_2}O\buildrel {Heat} \over \longrightarrow 6M + S{O_2} \uparrow $$
The metal (M) may be
$$2{M_2}S + 3{O_2}\buildrel {Heat} \over \longrightarrow 2{M_2}O + 2S{O_2} \uparrow $$
$${M_2}S + 2{M_2}O\buildrel {Heat} \over \longrightarrow 6M + S{O_2} \uparrow $$
The metal (M) may be
24
The white precipitate (Y), obtained on passing colorless and odourless gas (X) through an ammoniacal solution of NaCl, losses about 37% of its weight on heating and a white residue (Z) of basic nature is left. Identify (X), (Y) and (Z) from following sets.
25
Which structure has delocalised $$\pi$$-electrons?
26
The H3O+ ions has the following shape
27
For the reaction $$_7^{14}N(\alpha ,p)\,{}^{17}O$$, 1.16 MeV (Mass equivalent = 0.00124 amu) of energy is absorbed. Mass on the reactant side is 18.00567 amu and proton mass = 1.00782 amu. The atomic mass of $${}^{17}O$$ will be
28
A solution of NaNO3, when treated with a mixture of Zn dust and 'A' yields ammonia. 'A' can be
29
Indicate the number of unpaired electrons in K3[Fe(CN)6] and K4[Fe(CN)6].
30
Which of the following compounds have magnetic moment identical with [Cr(H2O)6]3+ ?
31
Among the following chlorides the compounds which will be hydrolysed most easily and most slowly in aqueous NaOH solution are respectively:
1. Methoxymethyl chloride
2. Benzyl chloride
3. Neopentyl chloride
4. Propyl chloride
1. Methoxymethyl chloride
2. Benzyl chloride
3. Neopentyl chloride
4. Propyl chloride
32
The products X and Y which are formed in the following sequence of reactions are respectively.
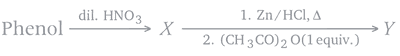
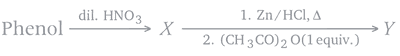
33
The atomic masses of helium and neon are 4.0 and 20.0 amu respectively. The value of the de-Broglie wavelength of helium gas at $$-$$73$$^\circ$$C is M times the de-Broglie wavelength of neon at 727$$^\circ$$C. The value of M is
34
The mole fraction of a solute in a binary solution is 0.1 at 298 K, molarity of this solution is same as its molality. Density of this solution at 298 K is 2.0 g cm$$-$$3. The ratio of molecular weights of the solute and the solvent (Msolute / Msolvent) is
35
5.75 mg of sodium vapour is converted to sodium ion. If the ionisation energy of sodium is 490 kJ mol$$-$$1 and atomic weight is 23 units, the amount of energy needed for this conversion will be
36
The product(s) in the following sequence of reactions will be
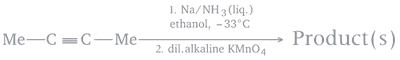
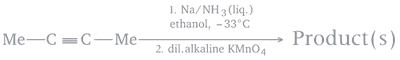
37
The compounds X and Y are respectively
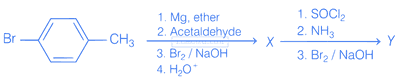

38
Aqueous solution of HNO3, KOH, CH3COOH and CH3COONa of identical concentration are provided. The pair(s) of solutions which form a buffer upon mixing is (are)
39
Reaction of silver nitrate solution with phosphorus acid produces
40
N2H4 and H2O2 show similarity in
Mathematics
1
If $$I = \mathop {\lim }\limits_{x \to 0} sin\left( {{{{e^x} - x - 1 - {{{x^2}} \over 2}} \over {{x^2}}}} \right)$$, then limit
2
Let f : R $$\to$$ R be such that f(0) = 0 and $$\left| {f'(x)} \right| \le 5$$ for all x. Then f(1) is in
3
If $$\int {{{\sin 2x} \over {{{(a + b\cos x)}^2}}}dx} = \alpha \left[ {{{\log }_e}\left| {a + b\cos x} \right| + {a \over {a + b\cos x}}} \right] + c$$, then $$\alpha$$ is equal to
4
Let $$g(x) = \int\limits_x^{2x} {{{f(t)} \over t}dt} $$ where x > 0 and f be continuous function and f(2x) = f(x), then
5
$$\int\limits_1^3 {{{\left| {x - 1} \right|} \over {\left| {x - 2} \right| + \left| {x - 3} \right|}}dx} $$ is equal to
6
The value of the integral $$\int\limits_{ - {1 \over 2}}^{{1 \over 2}} {{{\left\{ {{{\left( {{{x + 1} \over {x - 1}}} \right)}^2} + {{\left( {{{x - 1} \over {x + 1}}} \right)}^2} - 2} \right\}}^{1/2}}} dx$$ is equal to
7
If $$\int\limits_{{{\log }_e}2}^x {{{({e^x} - 1)}^{ - 1}}dx = {{\log }_e}{3 \over 2}} $$, then the value of x is
8
The normal to a curve at P(x, y) meets the X-axis at G. If the distance of G from the origin is twice the abscissa of P then the curve is
9
The differential equation of all the ellipses centred at the origin and have axes as the co-ordinate axes is where $$y^{\prime}\equiv{{{dx}\over {dy}}},y^{\prime\prime}\equiv{{{d^2}y\over {dx^2}}}$$
10
If $$x{{dy} \over {dx}} + y = {{xf(xy)} \over {f'(xy)'}}$$, then | f(xy) | is equal to (where k is an arbitrary positive constant).
11
The straight the through the origin which divides the area formed by the curves y = 2x $$-$$ x2, y = 0 and x = 1 into two equal halves is
12
The value of $$\int\limits_0^5 {\max \{ {x^2},6x - 8\} \,dx} $$ is
13
A bulb is placed at the centre of a circular track of radius 10 m. A vertical wall is erected touching the track at a point P. A man is running along the track with a speed of 10 m/sec. Starting from P the speed with which his shadow is running along the wall when he is at an angular distance of 60$$^\circ$$ from P is
14
Two particles A and B move from rest along a straight line with constant accelerations f and f' respectively. If A takes m sec. more than that of B and describes n units more than that of B in acquiring the same velocity, then
15
let $$\alpha$$, $$\beta$$, $$\gamma$$ be three non-zero vectors which are pairwise non-collinear. if $$\alpha$$ + 3$$\beta$$ is collinear with $$\gamma$$ and $$\beta$$ + 2$$\gamma$$ is collinear with $$\alpha$$ then $$\alpha$$ + 3$$\beta$$ + 6$$\gamma$$ is
16
Let f : R $$\to$$ R be given by f(x) = | x2 $$-$$ 1 |, x$$\in$$R. Then,
17
Let a, b, c be real numbers, each greater than 1, such that $${2 \over 3}{\log _b}a + {3 \over 5}{\log _c}b + {5 \over 2}{\log _a}c = 3$$. If the value of b is 9, then the value of 'a' must be
18
Consider the real valued function h : {0, 1, 2, ...... 100} $$\to$$ R such that h(0) = 5, h(100) = 20 and satisfying h(p) = $${1 \over 2}$$ {h(p + 1) + h(p $$-$$ 1)} for every p = 1, 2 ..... 99. Then the value of h(1) is
19
If |z| = 1 and z $$\ne$$ $$\pm$$ 1, then all the points representing $${z \over {1 - {z^2}}}$$ lie on
20
Let C denote the set of all complex numbers. Define A = {(z, w) | z, w$$\in$$C and |z| = |w|}, B = {z, w} | z, w$$\in$$C and z2 = w2}. Then
21
Let $$\alpha$$, $$\beta$$ be the roots of the equation x2 $$-$$ 6x $$-$$ 2 = 0 with $$\alpha$$ > $$\beta$$. If an = $$\alpha$$n $$-$$ $$\beta$$n for n $$\ge$$ 1, then the value of $${{{a_{10}} - 2{a_8}} \over {2{a_9}}}$$ is
22
For x$$\in$$R, x $$\ne$$ $$-$$1, if $${(1 + x)^{2016}} + x{(1 + x)^{2015}} + {x^2}{(1 + x)^{2014}} + ..... + {x^{2016}} = \sum\limits_{i = 0}^{2016} {{a_i}\,.\,{x^i}} $$, then a17 is equal to
23
Five letter words, having distinct letters, are to be constructed using the letters of the word 'EQUATION' so that each word contains exactly three vowels and two consonants. How many of them have all the vowels together?
24
What is the number of ways in which an examiner can assign 10 marks to 4 questions, giving not less than 2 marks to any question?
25
The digit in the unit's place of the number 1! + 2! + 3! + .... + 99! is
26
If M is a 3 $$\times$$ 3 matrix such that (0, 1, 2) M = (1 0 0), (3, 4 5) M = (0, 1, 0), then (6 7 8) M is equal to
27
Let $$A = \left( {\matrix{
1 & 0 & 0 \cr
0 & {\cos t} & {\sin t} \cr
0 & { - \sin t} & {\cos t} \cr
} } \right)$$
Let $$\lambda$$1, $$\lambda$$2, $$\lambda$$3 be the roots of $$\det (A - \lambda {I_3}) = 0$$, where I3 denotes the identity matrix. If $$\lambda$$1 + $$\lambda$$2 + $$\lambda$$3 = $$\sqrt 2 $$ + 1, then the set of possible values of t, $$-$$ $$\pi$$ $$\ge$$ t < $$\pi$$ is
Let $$\lambda$$1, $$\lambda$$2, $$\lambda$$3 be the roots of $$\det (A - \lambda {I_3}) = 0$$, where I3 denotes the identity matrix. If $$\lambda$$1 + $$\lambda$$2 + $$\lambda$$3 = $$\sqrt 2 $$ + 1, then the set of possible values of t, $$-$$ $$\pi$$ $$\ge$$ t < $$\pi$$ is
28
Let A and B two non singular skew symmetric matrices such that AB = BA, then A2B2(ATB)$$-$$1(AB$$-$$1)T is equal to
29
If an (> 0) be the nth term of a G.P. then
$$\left| {\matrix{ {\log {a_n}} & {\log {a_{n + 1}}} & {\log {a_{n + 2}}} \cr {\log {a_{n + 3}}} & {\log {a_{n + 4}}} & {\log {a_{n + 5}}} \cr {\log {a_{n + 6}}} & {\log {a_{n + 7}}} & {\log {a_{n + 8}}} \cr } } \right|$$ is equal to
$$\left| {\matrix{ {\log {a_n}} & {\log {a_{n + 1}}} & {\log {a_{n + 2}}} \cr {\log {a_{n + 3}}} & {\log {a_{n + 4}}} & {\log {a_{n + 5}}} \cr {\log {a_{n + 6}}} & {\log {a_{n + 7}}} & {\log {a_{n + 8}}} \cr } } \right|$$ is equal to
30
Let A, B, C be three non-void subsets of set S. Let (A $$\cap$$ C) $$\cup$$ (B $$\cap$$ C') = $$\phi$$ where C' denote the complement of set C in S. Then
31
Let T and U be the set of all orthogonal matrices of order 3 over R and the set of all non-singular matrices of order 3 over R respectively. Let A = {$$-$$1, 0, 1}, then
32
Four persons A, B, C and D throw and unbiased die, turn by turn, in succession till one gets an even number and win the game. What is the probability that A wins the game if A begins?
33
The mean and variance of a binomial distribution are 4 and 2 respectively. Then the probability of exactly two successes is
34
Let $${S_n} = {\cot ^{ - 1}}2 + {\cot ^{ - 1}}8 + {\cot ^{ - 1}}18 + {\cot ^{ - 1}}32 + ....$$ to nth term. Then $$\mathop {\lim }\limits_{n \to \infty } {S_n}$$ is
35
If a > 0, b > 0 then the maximum area of the parallelogram whose three vertices are O(0, 0), A(a cos$$\theta$$, b sin$$\theta$$) and B(a cos$$\theta$$, $$-$$ b sin$$\theta$$) is
36
Let A be the fixed point (0, 4) and B be a moving point on X-axis. Let M be the midpoint of AB and let the perpendicular bisector of AB meets the Y-axis at R. The locus of the midpoint P of MR is
37
A moving line intersects the lines x + y = 0 and x $$-$$ y = 0 at the points A, B respectively such that the area of the triangle with vertices (0, 0), A and B has a constant area C. The locus of the mid-point AB is given by the equation
38
The locus of the vertices of the family of parabolas $$6y = 2{a^3}{x^2} + 3{a^2}x - 12a$$ is
39
A ray of light along $$x + \sqrt 3 y = \sqrt 3 $$ gets reflected upon reaching X-axis, the equation of the reflected ray is
40
Two tangents to the circle x2 + y2 = 4 at the points A and B meet at M($$-$$4, 0). The area of the quadrilateral MAOB, where O is the origin is
41
From a point (d, 0) three normal are drawn to the parabola y2 = x, then
42
If from a point P(a, b, c), perpendicular PA and PB are drawn to YZ and ZX-planes respectively, then the equation of the plane OAB is
43
The co-ordinate of a point on the auxiliary circle of the ellipse x2 + 2y2 = 4 corresponding to the point on the ellipse whose eccentric angle is 60$$^\circ$$ will be
44
The locus of the centre of a variable circle which always touches two given circles externally is
45
A line with positive direction cosines passes through the point P(2, $$-$$1, 2) and makes equal angle with co-ordinate axes. The line meets the plane 2x + y + z = 9 at point Q. The length of the line segment PQ equals.
46
For $$y = {\sin ^{ - 1}}\left\{ {{{5x + 12\sqrt {1 - {x^2}} } \over {13}}} \right\};\left| x \right| \le 1$$, if $$a(1 - {x^2}){y_2} + bx{y_1} = 0$$ then (a, b) =
47
f(x) is real valued function such that 2f(x) + 3f($$-$$x) = 15 $$-$$ 4x for all x$$\in$$R. Then f(2) =
48
Consider the functions f1(x) = x, f2(x) = 2 + loge x, x > 0. The graphs of the functions intersect
49
The equation 6x + 8x = 10x has
50
Let f : D $$\to$$ R where D = [$$-$$0, 1] $$\cup$$ [2, 4] be defined by
$$f(x) = \left\{ {\matrix{ {x,} & {if} & {x \in [0,1]} \cr {4 - x,} & {if} & {x \in [2,4]} \cr } } \right.$$ Then,
$$f(x) = \left\{ {\matrix{ {x,} & {if} & {x \in [0,1]} \cr {4 - x,} & {if} & {x \in [2,4]} \cr } } \right.$$ Then,
51
Let f(x) be continuous periodic function with period T. Let $$I = \int\limits_a^{a + T} {f(x)\,dx} $$. Then
52
If $$b = \int\limits_0^1 {{{{e^t}} \over {t + 1}}dt} $$, then $$\int\limits_{a - 1}^a {{{{e^{ - t}}} \over {t - a - 1}}} $$ is
53
The differential of $$f(x) = {\log _e}(1 + {e^{10x}}) - {\tan ^{ - 1}}({e^{5x}})$$ at x = 0 and for dx = 0.2 is
54
Given that f : S $$\to$$ R is said to have a fixed point at c of S if f(c) = c. Let f : [1, $$\infty$$) $$\to$$ R be defined by f(x) = 1 + $$\sqrt x $$. Then
55
The $$\mathop {\lim }\limits_{x \to \infty } {\left( {{{3x - 1} \over {3x + 1}}} \right)^{4x}}$$ equals
56
The area bounded by the parabolas $$y = 4{x^2},y = {{{x^2}} \over 9}$$ and the straight line y = 2 is
57
If a($$\alpha$$ $$\times$$ $$\beta$$) + b($$\beta$$ $$\times$$ $$\gamma$$) + c($$\gamma$$ + $$\alpha$$) = 0, where a, b, c are non-zero scalars, then the vectors $$\alpha$$, $$\beta$$, $$\gamma$$ are
58
If the tangent at the point P with co-ordinates (h, k) on the curve y2 = 2x3 is perpendicular to the straight line 4x = 3y, then
59
The coefficient of a3b4c5 in the expansion of (bc + ca + ab)6 is
60
Three unequal positive numbers a, b, c are such that a, b, c are in G.P. while $$\log \left( {{{5c} \over {2a}}} \right),\log \left( {{{7b} \over {5c}}} \right),\log \left( {{{2a} \over {7b}}} \right)$$ are in A.P. Then a, b, c are the lengths of the sides of
61
The determinant $$\left| {\matrix{
{{a^2} + 10} & {ab} & {ac} \cr
{ab} & {{b^2} + 10} & {bc} \cr
{ac} & {bc} & {{c^2} + 10} \cr
} } \right|$$ is
62
Let R be the real line. Let the relations S and T or R be defined by
$$S = \{ (x,y):y = x + 1,0 < x < 2\} ,T = \{ (x,y):x - y$$ is an integer}. Then
$$S = \{ (x,y):y = x + 1,0 < x < 2\} ,T = \{ (x,y):x - y$$ is an integer}. Then
63
The plane lx + my = 0 is rotated about its line of intersection with the plane z = 0 through an angle $$\alpha$$. The equation changes to
64
The points of intersection of two ellipses $${x^2} + 2{y^2} - 6x - 12y + 20 = 0$$ and $$2{x^2} + {y^2} - 10x - 6y + 15 = 0$$ lie on a circle. The centre of the circle is
65
Let $$I = \int_{\pi /4}^{\pi /3} {{{\sin x} \over x}dx} $$. Then
66
If $$\left| {z + i} \right| - \left| {z - 1} \right| = \left| z \right| - 2 = 0$$ for a complex number z, then z is equal to
67
$$\left| {\matrix{
x & {3x + 2} & {2x - 1} \cr
{2x - 1} & {4x} & {3x + 1} \cr
{7x - 2} & {17x + 6} & {12x - 1} \cr
} } \right| = 0$$ is true for
68
The remainder when $${7^{{7^{{7^{{{..}^7}}}}}}}$$ (22 time 7) is divided by 48 is
69
Whichever of the following is/are correct?
70
A plane meets the co-ordinate axes t the points A, B, C respectively such a way that the centroid of $$\Delta$$ABC is (1, r, r2) for some real r. If the plane passes through the point (5, 5, $$-$$12) then r =
71
Let P be a variable point on a circle C and Q be a fixed point outside C. If R is the midpoint of the line segment PQ, then locus of R is
72
$$\mathop {\lim }\limits_{n \to \infty } \left\{ {{{\sqrt n } \over {\sqrt {{n^3}} }} + {{\sqrt n } \over {\sqrt {{{(n + 4)}^3}} }} + {{\sqrt n } \over {\sqrt {{{(n + 8)}^3}} }} + .... + {{\sqrt n } \over {\sqrt {{{[n + 4(n - 1)]}^3}} }}} \right\}$$ is
73
Let $$f(x) = \left\{ {\matrix{
{0,} & {if} & { - 1 \le x \le 0} \cr
{1,} & {if} & {x = 0} \cr
{2,} & {if} & {0 < x \le 1} \cr
} } \right.$$ and let $$F(x) = \int\limits_{ - 1}^x {f(t)dt} $$, $$-$$1 $$\le$$ x $$\le$$ 1, then
74
The greatest and least value of $$f(x) = {\tan ^{ - 1}} - {1 \over 2}\,ln \,x\,on\,\left[ {{1 \over {\sqrt 3 }},\sqrt 3 } \right]$$ are
75
Let f and g be periodic functions with the periods T1 and T2 respectively. Then f + g is
Physics
1
A spherical convex surface of power 5 D separates object and image space of refractive indices 1.0 and $$4\over3$$ , respectively. The radius of curvature of the surface is
2
In Young's double slit experiment, light of wavelength $$\lambda$$ passes through the double slit and forms interference fringes on a screen 1.2 m away. If the difference between 3rd order maximum and 3rd order minimum is 0.18 cm and the slits are 0.02 cm apart, then $$\lambda$$ is
3
A 12.5 eV electron beam is used to bombard gaseous hydrogen at ground state. The energy level upto which the hydrogen atoms would be excited is
4
Let r, v, E be the radius of orbit, speed of electron and total energy of electron respectively in H-atom. Which of the following quantities according to Bohr theory, is proportional to the quantum number n ?
5

What is the value of current through the diode in the circuit given?
6

For the given logic circuit, the output Y for inputs (A = 0, B = 1) and (A = 0, B = 0) respectively are
7
From dimensional analysis, the Rydberg constant can be expressed in terms of electric charge (e), mass (m) and Planck constant (h) as [consider $${1 \over {4\pi {\varepsilon _0}}} \equiv 1$$ unit]
8

Three blocks are pushed with a force F across a frictionless table as shown in figure above. Let N1 be the contact force between the left two blocks and N2 be the contact force between the right two blocks. Then,
9

A block of mass m slides with speed v on a frictionless table towards another stationary block of mass m. A massless spring with spring constant k is attached to the second block as shown in figure. The maximum distance, the spring gets compressed through is
10
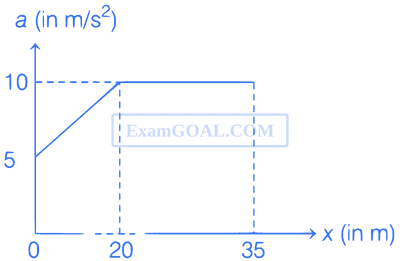
The acceleration versus distance graph for a particle moving with initial velocity 5 m/s is shown in the figure. The velocity of the particle at x = 35 m will be
11
A simple pendulum, consisting of a small ball of mass m attached to a massless string hanging vertically from the ceiling is oscillating with an amplitude such that Tmax = 2Tmin, where Tmax and Tmin are the maximum and minimum tension in the string, respectively. The value of maximum tension Tmax in the string is
12
In case of projectile motion, which one of the following figures represent variation of horizontal component of velocity (ux) with time t? (Assume that air resistance is negligible)
13
A uniform thin rod of length L, mass m is lying on a smooth horizontal table. A horizontal impulse P is suddenly applied perpendicular to the rod at one end. The total energy of the rod after the impulse is
14
Centre of mass (CM) of three particles of masses 1 kg, 2 kg and 3 kg lies at the point (1, 2, 3) and CM of another system of particles of 3 kg and 2 kg lies at the point ($$-$$1, 3, $$-$$2). Where should we put a particle of mass 5 kg, so that the CM of entire system lies at the CM of the first system?
15
A body of density 1.2 $$\times$$ 103 kg/m3 is dropped from rest from a height 1 m into a liquid to density 2.4 $$\times$$ 103 kg/m3. Neglecting all dissipative effects, the maximum depth to which the body sinks before returning to float on the surface is
16
Two solid spheres S1 and S2 of same uniform density fall from rest under gravity in a viscous medium and after sometime, reach terminal velocities v1 and v2, respectively. If ratio of masses $${{{m_1}} \over {{m_2}}} = 8$$, then $${{{v_1}} \over {{v_2}}}$$ will be equal to
17
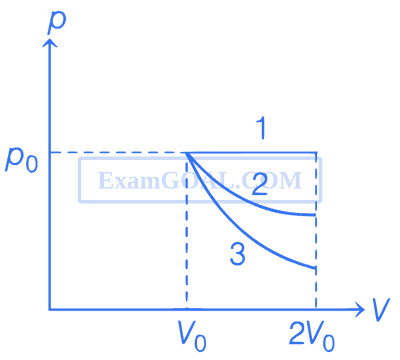
In the given figure, 1 represents isobaric, 2 represents isothermal and 3 represents adiabatic processes of an ideal gas. If $$\Delta$$U1, $$\Delta$$U2 and $$\Delta$$U3 be the changes in internal energy in these processes respectively, then
18
If pressure of real gas O2, in a container is given by $$p = {{RT} \over {2V - b}} - {a \over {4{b^2}}}$$, then the mass of the gas in the container is
19
300 g of water at 25$$^\circ$$C is added to 100 g of ice at 0$$^\circ$$C. The final temperature of the mixture is
20
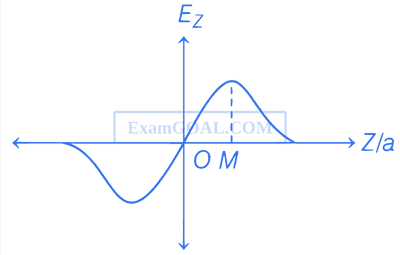
The variation of electric field along the Z-axis due to a uniformly charged circular ring of radius a in XY-plane as shown in the figure. The value of coordinate M will be
21
A metal sphere of radius R carrying charge q is surrounded by a thick concentric metal shell of inner and outer radii a and b, respectively. The net charge on the shell is zero. The potential at the centre of the sphere, when the outer surface of the shell is grounded will be
22
Three infinite plane sheets carrying uniform charge densities $$-$$ $$\sigma$$, 2$$\sigma$$, 4$$\sigma$$ are placed parallel to XZ-plane at Y = a, 3a, 4a respectively. The electric field at the point (0, 2a, 0) is
23
Two point charges +q1 and +q2 are placed a finite distance d apart. It is desired to put a third charge q3 in between these two charges, so that q3 is in equilibrium. This is
24

Consider two infinitely long wires parallel to Z-axis carrying same current I in the positive z-direction. One wire passes through the point L at coordinates ($$-$$1, +1) and the other wire passes through the point M at coordinates ($$-$$1, $$-$$1). The resultant magnetic field at the origin O will be
25
A thin charged rod is bent into the shape of a small circle of radius R, the charge per unit length of the rod being $$\lambda$$. The circle is rotated about its axis with a time period T and it is found the magnetic field at a distance d away (d >> R) from the centre and on the axis, varies as $$R^m \over d^n$$. The values of m and n respectively are
26

For two types of magnetic materials A and B, variation of $$1\over\chi$$ ($$\chi$$ : susceptibility) versus temperature T is shown in the figure. Then,
27
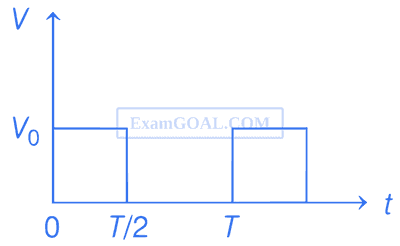
The rms value of potential difference V shown in the figure is
28
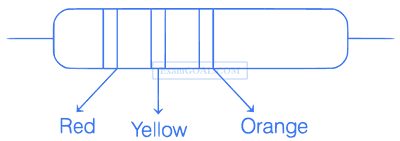
The carbon resistor with colour code is shown in the figure. There is no fourth band in the resistor. The value of the resistance is
29

Consider a pure inductive AC circuit as shown in the figure. If the average power consumed is P, then
30

The cross-section of a reflecting surface is represented by the equation x2 + y2 = R2 as shown in the figure. A ray travelling in the positive x-direction is directed toward positive y-direction after reflection from the surface at point M. The coordinate of the point M on the reflecting surface is
31
For a plane electromagnetic wave, the electric field is given by
$$ \overrightarrow{E} = 90\sin (0.5 \times {10^3}x + 1.5 \times {10^{11}}t)\widehat k$$ V/m. The corresponding magnetic field B will be
$$ \overrightarrow{E} = 90\sin (0.5 \times {10^3}x + 1.5 \times {10^{11}}t)\widehat k$$ V/m. The corresponding magnetic field B will be
32
Two metal wires of identical dimensions are connected in series. If $$\sigma$$1 and $$\sigma$$2 are the electrical conductivities of the metal wires respectively, the effective conductivity of the combination is
33
A uniform rod of length L pivoted at one end P is freely rotated in a horizontal plane with an angular velocity $$\omega$$ about a vertical axis passing through P. If the temperature of the system is increased by $$\Delta$$T, angular velocity becomes $${\omega \over 2}$$. If coefficient of linear expansion of the rod is $$\alpha$$($$\alpha$$ << 1), then $$\Delta$$T will be
34
An ideal gas of molar mass M is contained in a very tall vertical cylindrical column in the uniform gravitational field. Assuming the gas temperature to be T, the height at which the centre of gravity of the gas is located is (R$$\to$$universal gas constant)
35
Under isothermal conditions, two soap bubbles of radii a and b coalesce to form a single bubble of radius c. If the external pressure is p, then surface tension of the bubbles is
36

A small bar magnet of dipole moment M is moving with speed v along x-direction towards a small closed circular conducting loop of radius a with its centre O at x = 0 (see figure). Assume x >> a and the coil has a resistance R. Then, which of the following statements is/are true?
37
Electric field component of an EM radiation varies with time as E = a (cos$$\omega$$0t + sin$$\omega$$t cos$$\omega$$0t), where a is a constant and $$\omega$$ = 1015 s$$-$$1, $$\omega$$0 = 5 $$\times$$ 1015 s$$-$$1. This radiation falls on a metal whose stopping potential is $$-$$2 eV. Then, which of the following statements is/are true ? (h = 6.62 $$\times$$ 10$$-$$34 J-s)
38
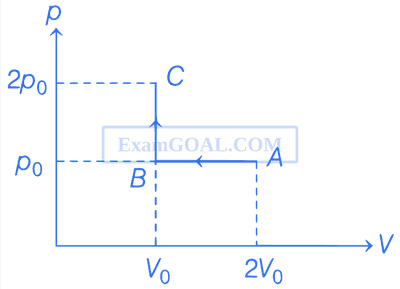
Consider the p - V diagram for 1 mole of an ideal monatomic gas shown in the figure. Which of the following statements is/are true?
39
The potential energy of a particle of mass 0.02 kg moving along X-axis is given by V = Ax (x $$-$$ 4) J, where x is in metre and A is a constant. Which of the following statements is/are correct?
40
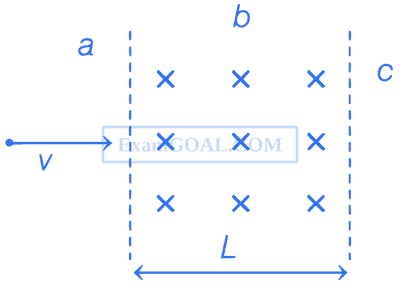
A particle of mass m and charge q moving with velocity v enters region-b from region-a along the normal to the boundary as shown in the figure. Region-b has a uniform magnetic field B perpendicular to the plane of the paper. Also, region-b has length L.
Choose the correct statement.