KCET 2017
Paper was held on
Tue, May 2, 2017 5:00 AM
Chemistry
1
The reaction quotient ' $Q$ ' is useful inpredicting the direction of the reaction. Which of the following is incorrect?
2
Square planar complex of the type $M_{\text {AXBL }}$ (where $A, B, X$ and $L$ ) are unidenate ligands shows following set of isomers
3
By passing electric current, $\mathrm{NaClO}_3$ is converted in to $\mathrm{NaClO}_4$ according to the following equation
$$ \mathrm{NaClO}_3+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{NaClO}_4+\mathrm{H}_2 $$
How many moles of $\mathrm{NaClO}_4$ will be formed when three Faradays of charges is passed through $\mathrm{NaClO}_3$ ?
4
The pressure of real gases is less than that of ideal gas because of
5
Which of the following reagent cannot be used to oxidise primary alcohols to aldehydes?
6
The product formed during the following reaction are
7
Bactericidal antibiotics among the following is
8
Which of the following is not a biodegradable polymer?
9
Reduction of ketones cannot be carried out with which of the following reagents?
10
Which of the following structure of a molecule is expected to have three bond pairs and one lone pair of electrons?
11
The standard reduction potential at 298 K for the following half cell reaction
$$ \begin{aligned} & 2 \mathrm{n}^{2+}(a q)+2 e^{-} \rightarrow \mathrm{Zn}(s) ; E^0=-0.762 \mathrm{~V} \\ & \mathrm{Cr}^{3+}(a q)+3 e^{-} \rightarrow \mathrm{Cr}(s) ; E^0=0.740 \mathrm{~V} \\ & 2 \mathrm{H}^{+}(a q)+2 e^{-} \rightarrow \mathrm{Hz}(g) ; E^0=0.0 \mathrm{~V} \\ & \mathrm{~F}_2(g)+2 e^{-} \rightarrow 2 \mathrm{~F}^{-}(a q) ; E^0=2.87 \mathrm{~V} \end{aligned} $$
Which of the following is strongest reducing agent?
12
Plaster of Paris is represented as
13
Toluene reacts with halogen in presence of iron (III) chloride giving ortho and para halo compounds. The reaction is
14
In a face centred cubic arrangement of $A$ and $B$ atoms in which ' $A$ ' atoms are at the corners of the unit cell and ' $B$ ' atoms are at the face centres. One of the ' $A$ ' atoms is missing from one corner in unit cell.The simplest formula of compounds is
15
The correct order of increasing basic nature for the bases $\mathrm{NH}_3, \mathrm{CH}_3 \mathrm{NH}_2$ and $\left(\mathrm{CH}_3\right)_2 \mathrm{NH}$ in aqueous solutions
16
The electronegativities of $\mathrm{C}, \mathrm{N}, \mathrm{Si}$ and P are in the order of
17
For a reaction $\frac{1}{2} A \rightarrow 2 B$ rate of disappearance of $A$ is related to rate of appearance of $B$ by the expression
18
Which of the following statement is incorrect?
19
The coordination number and the oxidation state of the. element ' $M$ ' in the complex $\left[\mathrm{M}(e n)_2\left(\mathrm{C}_2 \mathrm{O}_4\right)\right] \mathrm{NO}_2$ {where (en) is ethan1, 2-diamine) are respectively
20
Select wrong chemical reaction among the following.
21
If $3.01 \times 10^{20}$ molecules are removed from 98 mg of $\mathrm{H}_2 \mathrm{SO}_4$, then number of moles of $\mathrm{H}_2 \mathrm{SO}_4$ left are
22
Which of the following elements forms $p_\pi-p_\pi$ bond with itself?
23
Which of the following statement is in accordance with the Arrhenius equations?
24
The glycosidic linkage present in sucrose is between
25
A reaction has both $\Delta H$ and $\Delta S$ -ve. The rate of reaction
26
Addition of mineral acid to an aqueous solution of borax, the following compound is formed
27
The magnetic nature of elements depends on the presence of unpaired electrons. Identify the configuration of transition elements which shows highest magnetic moment?
28
The process which is responsible for the formation of delta at a place where rivers meets the sea is
29
Extraction of chlorine from brine solution is based on
30
Lower members of aliphatic carboxylic acid are soluble in water. This is due to
31
Which one of the following is not a common component of photo-chemical smog?
32
Which of the following is not a favourable condition for physical adsorption?
33
The correct statement regarding defect in solids is
34
According to crystal field theory, the $M-L$ bond in a complex is
35
Which of the following crystal has unit cell such that $a \neq b \neq c$ and $\alpha \neq \beta \neq \gamma \neq 90^{\circ}$ ?
36
Which of the following statement is wrong regarding lanthanoids?
37
Hormones are secreted by ductless glands of human body. Iodine containing hormone is
38
The, vant Hoff's factor ' $\boldsymbol{i}$ ' accounts for
39
In which of the following, homolytic bond fission takes place?
40
The correct set of quantum number for the unpaired electrons of chlorine atom is
41
Which of the following metallic oxide exhibit amphoteric nature?
42
Which one of the following noble gas has an unusual property of diffusing through the materials such as rubber, glass or plastic?
43
When the pure solvent diffuses out of the solution through the semi-permeable membrane then the process is called
44
Cannizzaro's reaction is an example of auto oxidation
45
The equilibrium constant for the reaction $\mathrm{N}_2(g)+\mathrm{O}_2(g) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g})$ is $4 \times 10^{-4}$ at 2000 K . In presence of a catalyst the equilibrium is attained ten times faster. Therefore the equilibrium constant in presence of catalyst 2000 K is
46
Which of the following is correct electron dot structure of $\mathrm{N}_2 \mathrm{O}$ molecule?
47
Pick the correct statement among the following statement.
48
Pick the wrong statements from the following.
49
Which of the following order is true regarding the acidic nature of phenol?
50
Identify the correct statement in the following.
51
Galbriel phthalimide synthesis is used in the preparation of primary amine from phthalimide, which of the following reagent is not used during the process?
52
$3 \mathrm{ClO}^{-}(a q) \longrightarrow \mathrm{ClO}^{-}+2 \mathrm{Cl}^{-}$is an example of
53
Hydrogenation of vegetable oils in presence of finely divided nickel as catalyst.The reaction is
54
In the manufacture of hydrogen from water gas $\left(\mathrm{CO}+\mathrm{H}_2\right)$, which of the following is correct statement?
55
In the following sequence of reactions
$$ \mathrm{CH}_3 \mathrm{Br} \xrightarrow{\mathrm{KCN}} A \xrightarrow{\mathrm{H}_3 \mathrm{O}^{-}} B \xrightarrow{\mathrm{LiAl} / \mathrm{H}_4} $$
The end product $C$ is
56
The monomer used in novolac, a polymer used in paints
57
For the preparation of alkanes, aqueous solution of sodium of potassium salt of carboxylic acid is subjected to
58
Which of the following aqueous solution has highest freezing point?
59
In the electrolysis of aqueous sodium chloride solution, which of the half cell reaction will occur at anode?
60
The metal extracted by leaching with a cyanide is
Mathematics
1
If an LPP admits optimal solution at two consecutive vertices of a feasible region, then
2
$$
\text { } \begin{aligned}
Let\,\,\,\Delta & =\left|\begin{array}{lll}
A x & x^2 & 1 \\
B y & y^2 & 1 \\
C z & z^2 & 1
\end{array}\right| \text { and }
\Delta_1 =\left|\begin{array}{ccc}
A & B & C \\
x & y & z \\
z y & z x & x y
\end{array}\right| \text {, then }\left|\begin{array}{ccc}
A x & B y & C y \\
x^2 & y^2 & z^2 \\
1 & 1 & 1
\end{array}\right|
\end{aligned}
$$
3
The total number of terms in the expansion of $(x+a)^{47}-(x-a)^{47}$ after simplification is
4
The function $f(x)=x^2+2 x-5$ is strictly increasing in the interval
5
The shaded region in the figure is the solution set of the inequations
6
The point on the curve $y^2=x$ where the tangent makes an angle of $\pi / 4$ with $X$-axis is
7
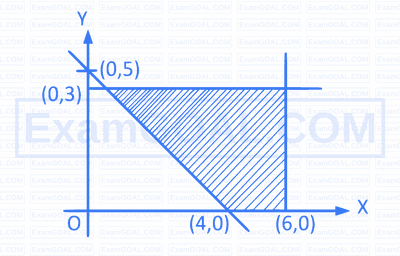
$$ \int\limits_{-\pi / 2}^{\pi / 2} \frac{d x}{e^{\sin x}+1} $$
8
If $a$ and $\mathbf{b}$ are unit vectors, then angle between $\mathbf{a}$ and $\mathbf{b}$ for $\sqrt{3} \mathbf{a}-\mathbf{b}$ to be unit vector is
9
The contrapositive statement of the statement "If $x$ is prime number, then $x$ is odd" is
10
$\int\limits_{-5}^5|x+2| d x$ is equal to
11
If $\left|\begin{array}{ll}3 & x \\ x & 1\end{array}\right|=\left|\begin{array}{ll}3 & 2 \\ 4 & 1\end{array}\right|$, then $x$ is equal to
12
If $2\left|\begin{array}{ll}1 & 3 \\ 0 & x\end{array}\right|+\left|\begin{array}{ll}y & 0 \\ 1 & 2\end{array}\right|=\left|\begin{array}{ll}5 & 6 \\ 1 & 8\end{array}\right|$, then the value of $x$ and $y$ are
13
$$ \int\limits_0^{\pi / 2} \frac{1}{a^2 \cdot \sin ^2 x+b^2 \cdot \cos ^2 x} d x $$
14
$$ \int \sqrt{x^2+2 x+5} d x \text { is equal to } $$
15
A box has 100 pens of which 10 are defective. The probability that out of a sample of 5 pens drawn one by one with replacement and atmost one is defective, is
16
The range of $\sec ^{-1} x$ is
17
$\int \frac{(x+3) e^x}{(x+4)^2} d x$ is equal to
18
$$ \text { If } y=\left|\begin{array}{ccc} f(x) & g(x) & h(x) \\ l & m & n \\ a & b & c \end{array}\right| \text {, then } \frac{d y}{d x} \text { is equal to } $$
19
General solution of differential equations
$\frac{d y}{d x}+y=1(y \neq 1)$ is
20
If $A$ is a square matrix of order $3 \times 3$, then $|K A|$ is equal to
21
If $A=\frac{1}{\pi}\left|\begin{array}{ll}\sin ^{-1}(\pi x) & \tan ^{-1}\left(\frac{x}{\pi}\right) \\ \sin ^{-1}\left(\frac{x}{\pi}\right) & \cot ^{-1}(\pi x)\end{array}\right|$
$B=\left|\begin{array}{cc}-\cos ^{-1}(\pi x) & \tan ^{-1}\left(\frac{x}{\pi}\right) \\ \sin ^{-1}\left(\frac{x}{\pi}\right) & -\tan ^{-1}(\pi x)\end{array}\right|$,
then $A-B$ is :
22
If ${ }^n C_{12}={ }^n C_8$, then $n$ is equal to
23
The probability distribution of $X$ is
$$ \begin{array}{|c|l|c|c|c|} \hline \boldsymbol{X} & 0 & 1 & 2 & 3 \\ \hline \boldsymbol{P}(\boldsymbol{X}) & 0.3 & k & 2 k & 2 k \\ \hline \end{array} $$
$$ \text { The value of } k \text { is } $$24
The degree of the differential equation $\left[1+\left(\frac{d y}{d x}\right)^2\right]^2=\frac{d^2 y}{d x^2}$ is
25
$3+5+7+\ldots$ to $n$ terms is
26
$\int \frac{\cos 2 x-\cos 2 \theta}{\cos x-\cos \theta} d x$ is equal to
27
If $A$ and $B$ are finites sets and $A \subset B$, then
28
$$The\,\,value\,\,of\,\,\mathop {\lim }\limits_{\theta \to 0} {{1 - \cos 4\theta } \over {1 - \cos 6\theta }}\,\,is$$
29
If $\mathbf{a}=2 \hat{\mathbf{i}}+\lambda \hat{\mathbf{j}}+\hat{\mathbf{k}}$ and $\mathbf{b}=\hat{\mathbf{i}}+2 \hat{\mathbf{j}}+3 \hat{\mathbf{k}}$ are orthogonal, then value of $\lambda$ is
30
If $f(x)=\left\{\begin{array}{cll}k x^2 & \text { if } & x \leq 2 \\ 3 & \text { if } & x>2\end{array}\right.$ is continuous at $x=2$, then the value of $k$ is
31
The area of triangle with vertices $(K, 0),(4,0)$, $(0,2)$ is 4 sq units, then value of $K$ is
32
If $\left(\frac{1+i}{1-i}\right)^m=1$, then the least positive integral value of $m$ is
33
If $\mathbf{a}, \mathbf{b}, \mathbf{c}$ are unit vectors such that $a+b+c=0$, then the value of $\mathbf{a} \cdot \mathbf{b}+\mathbf{b} \cdot \mathbf{c}+\mathbf{c} \cdot \mathbf{a}$ is equal to
34
The value of $\cos ^2 45^{\circ}-\sin ^2 15^{\circ}$ is
35
Let $f: R \rightarrow R$ be defined by $f(x)=x^4$, then
36
If $\sin x=\frac{2 t}{1+t^2}, \tan y+\frac{2 t}{1-t^2}$, then $\frac{d y}{d x}$ is equal to
37
The plane $2 x-3 y+6 z-11=0$ makes an angle $\sin ^{-1}(\alpha)$ with $X$-axis, the value of $\alpha$ is equal to
38
If $f(x)=8 x^3, g(x)=x^{1 / 3}$, then $f \circ g(x)$ is
39
If $y=\log (\log x)$, then $\frac{d^2 y}{d x^2}$ is equal to
40
$\int\limits_{0.2}^{3.5}[x] d x$ is equal to :
41
If $|x-2| \leq 1$, then
42
The perpendicular distance of the point $P(6,7,8)$ from $X Y$-plane is
43
Binary operation * on $R-\{-1\}$ defined by $a^* b=\frac{a}{b+1}$ is
44
If $y=\tan ^{-1}\left(\frac{\sin x+\cos x}{\cos x-\sin x}\right)$, then $\frac{d y}{d x}$ is equal to
45
The eccentricity of the ellipse $\frac{x^2}{36}+\frac{y^2}{16}=1$ is
46
The integrating factor of the differential equation
$x \cdot \frac{d y}{d x}+2 y=x^2$ is $(x \neq 0)$
47
The derivative of $\cos ^{-1}\left(2 x^2-1\right)$ w.r.t. $\cos ^{-1} x$ is
48
The rate of change of volume of a sphere with respect to its surface area when the radius is 4 cm is
49
$\int\limits_0^{\pi / 2} \frac{\tan ^7 x}{\cot ^7 x+\tan ^7 x} d x$ is equal to
50
The range of the function $f(x)=\sqrt{9-x^2}$ is
51
Reflexion of the point $(\alpha, \beta, \gamma)$ in $X Y$-plane is
52
The area of the region bounded by the curve $y=x^2$ and the line $y=16$
53
If coefficient of variation is 60 and standard deviation is 24 , then Arithmetic mean is
54
Two events $A$ and $B$ will be independent if
55
Area of the region bounded by the curve $y=\cos x, x=0$ and $x=\pi$ is
56
The value of $c$ in mean value theorem for the function $f(x)=x^2$ in $[2,4]$ is
57
Equation of line passing through the point $(1,2)$ and perpendicular to the line $y=3 x-1$
58
If $\tan ^{-1} x+\tan ^{-1} y=\frac{4 \pi}{5}$, then $\cot ^{-1} x+\cot ^{-1} y$ is equal to
59
If a matrix $A$ is both symmetric and skew symmetric, then
60
The distance of the point $(-2,4,-5)$ from the line $\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}$ is
Physics
1
A coil of inductive reactance $1 / \sqrt{3} \Omega$ and resistance $1 \Omega$ is connected to a $200 \mathrm{~V}, 50 \mathrm{~Hz}$ AC supply. The time lag between maximum voltage and current is
2
A car moving with a velocity of $20 \mathrm{~ms}^{-1}$ stopped at a distance of 40 m . If the same car is travelling at double the velocity, the distance travelled by it for same retardation is
3
The particle emitted in the decay of ${ }_{92}^{238} \mathrm{U}$ to ${ }_{92}^{234} \mathrm{U}$
4
Of the following graphs, the one that correctly represents the $I-V$ characteristics of a 'Ohmic device' is
5
The susceptibility of a ferromagnetic substance is
6
The working of magnetic braking of trains is based on
7
A substance of mass 49.53 g occupies $1.5 \mathrm{~cm}^3$ of volume. The density of the substance (in $\mathrm{g} \mathrm{cm}^{-3}$ ) with correct number of significant figures is
8
From the following graph of photo current against collector plate potential, for two different intensities of light $I_1$ and $I_2$, one can conclude
9
Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls when in air
10
If $\mathbf{E}$ and $\mathbf{B}$ represent electric and magnetic field vectors of an electromagentic wave, the direction of propagation of the wave is along
11
A body of the mass 50 kg is suspended using a spring balance inside a lift at rest. If the lift starts falling freely, the reading of the spring balance is
12
Two point charges $A=+3 \mathrm{nC}$ and $B=+1 \mathrm{nC}$ are placed 5 cm apart in air. The work done to move charge $B$ towards $A$ by 1 cm is
13
A proton, a deuteron and an $\alpha$-particle are projected perpendicular to the direction of a uniform magnetic field with same kinetic energy. The ratio of the radii of the circular paths described by them is
14
The S.I. unit of specific heat capacity is
15
In the three parts of a transistor, 'Emitter' is of
16
A bar magnet is allowed to fall vertically through a copper coil placed in a horizontal plane. The magnet falls with a net acceleration, is
17
For which combination of working temperatures, the efficiency of Carnot's engine is the least?
18
A basic communication system consists of
(i) Transmitter
(ii) Information sources
(iii) User of information
(iv) Channel
(v) Receiver
19
According to Huygens' principle, during refraction of light from air to a denser medium
20
A galvanometer of resistance $50 \Omega$ is connected to a battery of $3 \cdot \mathrm{~V}$ along with a${ }^{\text { }}$ resistance of $2950 \Omega$ in series shows full-scale deflection of 30 divisions. The additional series resistance required to reduce the deflection to 20 divisions is
21
In the A.C. circuit shown, keeping ' $K$ ' pressed, if an iron rod inserted into the coil, the bulb in the circuit,
22
A magnetic dipole of magnetic moment $6 \times 10^{-2}$ A-m ${ }^2$ and moment of inertia $12 \times 10^{-6} \mathrm{~kg}-\mathrm{m}^2$ performs oscillations in a magnetic field of $2 \times 10^{-2} \mathrm{~T}$. The time taken by the dipole to complete 20 oscillations is ( $\pi \approx 3$ )
23
$4 \times 10^{10}$ electrons are removed from a neutral metal sphere of diameter 20 cm placed in air. The magnitude of the electric field (in $\mathrm{NC}^{-1}$ ) at a distance of 20 cm from its centre is
24
The mass defect of ${ }_2^4 \mathrm{He}$ is 0.03 u . The binding energy per nucleon of helium (in MeV) is
25
A cylindrical conductor of diameter 0.1 mm carries a current of 90 mA . The current density ( in $\mathrm{Am}^{-2}$ ) is ( $\pi \approx 3$ )
26
Which of the following properties is 'False' for a bar magnet?
27
According to cartesian sign convention, in ray optics
28
A linear object of height 10 cm is kept in front of a concave mirror of radius of curvature 15 cm , at a distance of 10 cm . The image formed is
29
The energy gap in case of which of the following is less than 3 eV ?
30
The minimum value of effective capacitance that can be obtained by combining 3 capacitors of capacitances $1 \mathrm{pF}, 2 \mathrm{pF}$ and 4 pF
31
Two spheres of electric charges +2 nC and -8 nC are placed at a distance $d$ apart. If they are allowed to touch each other, what is the new distance between them to get a repulsive force of same magnitude as before?
32
The value of acceleration due to gravity at a depth of 1600 km is equal to
33
Two simple pendulums $A$ and $B$ are made to oscillate simultaneously and it is found that $A$ completes 10 oscillations in 20 sec and $B$ completes 8 oscillations in 10 sec . The ratio of the length of $A$ and $B$ is
34
A motor pump lifts 6 tonnes of water from a well of depth 25 m to the first floor of height 35 m from the ground floor in 20 minutes. The power of the pump (in kW ) is $\left[g=10 \mathrm{~ms}^{-2}\right.$ ]
35
The waves set up in a closed pipe are
36
In the figure shown, if the diode forward voltage drop is 0.2 V , the voltage difference between $A$ and $B$ is
37
If $\mathbf{A}=2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}}+8 \hat{\mathbf{k}}$ is perpendicular to $\mathbf{B}=4 \hat{\mathbf{j}}-4 \hat{\mathbf{i}}+\alpha \hat{\mathbf{k}}$, then the value of $\alpha$ is
38
The angle between velocity and acceleration of a particle describing uniform circular motion is
39
A straight wire of length 50 cm carrying a current of 2.5 A is suspended in mid-air by a uniform magnetic field of 0.5 T (as shown in figure). The mass of the wire is ( $g=10 \mathrm{~ms}^{-2}$ )
40
'Young's modulus' is defined as the ratio of
41
Which of the following semi-conducting device is used as voltage regulator?
42
Which of the following logic gate is universal gate
43
A particle is dropped from a height $H$. The de-Broglie wavelength of the particle depends on height as
44
Three point charges of $+2 q,+2 q$ and $-4 q$ are placed at the corners $A, B$ and $C$ of an equilateral triangle $A B C$ of side $x$. The magnitude of the electric dipole moment of this system is
45
In a system of two crossed polarisers, it is found that the intensity of light from the second polariser is half from that of first polariser. The angle between their pass axes is
46
A piece of copper is to be shaped into a conducting wire of maximum resistance. The suitable length and diameter are ......................and............................respectively.
47
During scattering of light, the amount of scattering in inversely proportional to................ of wavelength of light.
48
A jet plane of wing span 20 m is travelling towards west at a speed of $400 \mathrm{~ms}^{-1}$. If the earth's total magnetic field is $4 \times 10^{-4} \mathrm{~T}$ and the dip angle is $30^{\circ}$, at that place, then the voltage differences developed across the ends of the wing is
49
The energy (in eV ) required to excite an electron from $n=2$ to $n=4$ state in hydrogen atom is
50
'Hydraulic lift' works on the basis of
51
In a nuclear reactor, the function of the moderator is to decreases
52
The scientist who is credited with the discovery of 'nucleus' in an atom is
53
A system of two capacitors of capacitance $2 \mu \mathrm{~F}$ and $4 \mu \mathrm{~F}$ is connected in series across a potential difference of 6 V . The electric charge and energy stored in a system are
54
In meter bridge experiment, with a standard resistance in the right gap and a resistance coil dipped in water (in a beaker) in the left gap, the balancing length obtained is ' $l$ '. If the temperature of water is increased, the new balancing
55
The power dissipated in $3 \Omega$ resistance in the following circuit is
56
The mean energy of a molecule of an ideal gas is
57
The magnetic field at the centre of a current carrying loop of radius 0.1 m is $5 \sqrt{5}$ times that at a point along its axis. The distance of this point from the centre of the loop is
58
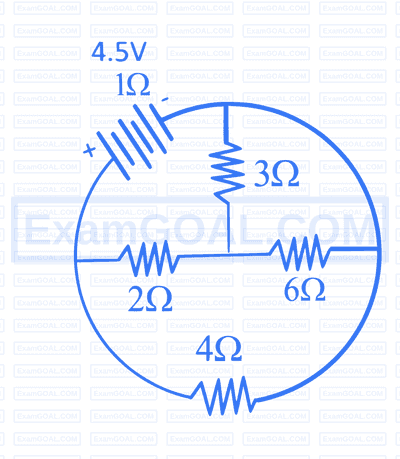
$$ \text { The value of } I \text { in the figure shown below is } $$
59
In Young's double-slit experiment, if yellow light is replaced by blue light, the interference fringes becomes
60
The output of a step down transformers is measured to be 48 V when connected to a 12 W bulb. The value of peak current is